Introduction

Measurement equivalent/invariance (ME/I) concerns whether the relationship between the targeted latent variable and the observed items are identical across groups (Millsap, 2012). ME/I is an important psychometric property, which ensures that the results obtained from a construct measure are comparable and generalizable across groups (Brown, 2014). Failure to achieve ME/I can lead to biased comparisons or selections across groups (Chen, 2008; Millsap & Kwok, 2004; Steinmetz, 2013).

Evaluating ME/I properties of a scale is a complex issue. There are various basic levels of ME/I, representing more or less restricted levels of invariance (explained in detail below). Thus, ME/I is typically examined through a series of Chi-square difference tests (Δχ2 tests) between nested invariance models (representing different levels of ME/I) using multiple group confirmatory analysis (MG-CFA) (Vandenberg, & Lance, 2000). If a certain basic level of ME/I is not achieved, indicating that one or more items are not invariant across groups, researchers can follow up with a specification search for the problematic items and release implausible constraints correspondingly. In the current study, we refer to this kind of specification search as sequential backward specification search (SBSS).

The appropriate methods for specification search vary depending on the nature of the item-level data. Considering the popularity of Likert-type scales in social and behavioral sciences, the items are often ordinal in nature. In addition, missing data are likely to occur due to nonresponse or planned missing data designs. To our knowledge, although specification search methods have been studied with ordinal complete data (Oort, 1998; Yoon & Kim, 2014), no research on those methods has considered missing ordinal data.

In practice, three estimation methods have been used to conduct SBSS when ordinal missing data present. These methods include full information maximum likelihood (FIML), robust full information maximum likelihood (rFIML), and the mean and variance adjusted weighted least-squared method paired with pairwise deletion (WLSMV_PD) (e.g., Beam, Marcus, Turkheimer & Emery, 2018; Bou Malham & Saucier, 2014; Fokkema, Smits, Kelderman, & Cuijpers, 2013; Sommer, et al., 2019). Given that previous research has shown that rFIML outperformed FIML for ordinal data (e.g., Chen, Wu, Garnier-Villarreal, Kite & Jia, 2019), we only consider rFIML and WLSMV_PD in the current study.

In theory, rFIML and WLSMV_PD have their own advantages and limitations. rFIML is capable of utilizing all available information for model estimation, but it assumed ordinal data to be continuous. WLSMV_PD, on the other hand, correctly accounts for the ordinal nature of the data, but it uses pairwise deletion (PD) to handle missing data, which is less optimal than a full information method (Savalei & Bentler, 2005).

Given that neither of the methods is ideal theoretically, it would be interesting to know how they perform in SBSS and which one would be better. The goal of the current study is thus to examine the relative performance of the two methods in SBSS with ordinal missing data. The rest of the article is organized as follows. We first review necessary background information for the study, including a typical ME/I test process and specification search methods. We then explain how rFIML and WLSMV_PD work and present designs for the simulation study. Finally, we report the result from the simulation study and provide practical recommendations to empirical researchers based on our results. We conclude the article by discussing limitations of the current study and potential directions for future research.

A typical ME/I testing procedure with MG-CFA

There are four basic levels of ME/I, namely, configural, metric, scalar, and strict invariance, representing the least restricted invariance model to the most restricted invariance model, respectively. When the configural invariance model is examined, the same CFA model is fit to groups, with model parameters allowed to vary across groups. The metric invariance model is simply the configural invariance model with equality constraints on all factor loadings across groups. The scalar invariance model adds equality constraints on intercepts/thresholds across groups. Finally, equality constraints on corresponding residual variances are further included into the scalar invariance model to create a strict invariance model (Gregorich, 2006).

These four basic ME/I models are nested and thus are usually evaluated in sequence to decide which level of ME/I is achieved, starting from the configural invariance model. If the configural invariance fits the data, then a Chi-square difference (Δχ2) test comparing it to the metric invariance model will be conducted. A non-significant Δχ2 test would indicate that the metric invariance model passes. Researchers can further test scalar invariance by comparing it to the metric invariance model through another Δχ2 test, and so on (Byrne, 2013). On the other hand, a significant Δχ2 test would suggest that imposing equality constraints on all target parameters are implausible, and at least one target parameter is not equal (non-invariant) across groups.

Partial invariance models

The four types of ME/I models described above are considered “full” invariance models, given that equality constraints are placed on all parameters of the same type (e.g., all loadings) across groups (Jung & Yoon, 2016). When a full invariance model is rejected, one could establish a partial invariance model by releasing equality constraints on some but not all of the target parameters (Byrne, Shavelson, & Muthén, 1989; Millsap, 2012; Putnick, & Bornstein, 2016; Schmitt & Kuljanin, 2008). For instance, a partial scalar invariance model will be a model with some of the intercepts/thresholds varying across groups.

Past research has demonstrated the importance of correctly identifying non-invariant items in partial invariance models. On one hand, failing to release wrong equality constraints could distort the estimated latent mean differences across groups (Shi, Song, & Lewis, 2017a) and group comparisons (e.g., French and Finch, 2016). On the other hand, imposing equality constraints on invariant parameters can improve the statistical power of detecting latent mean differences across groups (Xu & Green, 2016). Shi, Song, and Lewis (2017a) also showed that in comparison to models with only one correctly specified invariant item, partial invariance models with multiple correctly specified equality constraints could generate more accurate and efficient estimates (e.g., factor means and factor loadings).

Sequential backward specification search for partial invariance models

Establishing a correct partial invariance model involves an iterative process of specification search for non-invariant parameters. Ideally, this search should be guided by both theory and statistical criteria. In practice, however, it often relies solely on statistical criteria (Yoon & Kim, 2014). Multiple specification search methods have been proposed (e.g., Huang, 2018; Jung & Yoon, 2016; Yoon & Millsap, 2007; Shi, Song, Liao, Terry, & Snyder 2017b). These methods basically fall into two categories: forward search and backward search methods. Forward search methods start the search with a model that does not contain any equality constraints on target parameters, while backward search methods start the search with a model with equality constraints on all target parameters. In a partial scalar invariance model, for example, a forward search method will start the search from the full metric invariance model, while a backward search method will start with the full scalar invariance model, which is the model that has been rejected. Note that the definitions above are provided by previous research that focuses on the search for partial invariance models (Jung & Yoon, 2016); while if one adopts the definitions that the backward search means to initiate the search from a more general model (e.g., Chou & Bentler, 2002), the search starts with a full invariance model with equality constraints on all target parameters will then become a “forward” search method instead.

In addition, different statistical criteria are used in the two types of search methods. Forward specification search usually relies or statistics such as confidence intervals (CI). Backward search methods, in comparison, often use modification indices (MFI) to identify implausible equality constraints (e.g., Byrne, 2013; Yoon & Millsap, 2007; Byrne et al. 1989; Oort, 1998; Yoon & Millsap, 2007). MFI measures the decrease in the Chi-square test statistic (i.e., improvement in goodness of fit) when a fixed parameter or an equality constraint is freed (Sörbom, 1989). MFI is assumed to follow a Chi-square distribution with df = 1. The search starts with releasing the equality constraint which has the largest MFI among all significant constraints (i.e., constraints with MFI > 3.841, the critical value of a χ2 statistic with df =1 and α = 0.05), and then refits the model to identify the second equality constraint to release. The search process continues until none of the MFIs for the remaining equality constraints is significant, or until there is no need for model modification because of a good overall model fit indicated by global fit indices such as a non-significant χ2 test (p < 0.05). (Kim & Yoon, 2014; Yoon & Millsap, 2007). This sequential search procedure is referred to as the sequential backward specification search method with the largest MFI (SBSS_LMFI).

Among the available search methods, SBSS_LMFI is not only one of the most widely used methods (Kim & Yoon, 2014) but also one of the few search methods that have been validated across continuous and ordinal indicators (e.g., Jung & Yoon, 2016; Kim & Yoon, 2014; Whittaker & Khojasteh, 2013; Yoon & Millsap, 2007). Thus, we believe it will be a good starting point for us to study the missing data issues in specification search. The other specification search methods will be briefly discussed at the end of the article.

Methods to handle ordinal missing data in SBSS_LMFI

Even though SBSS_LMFI has been validated with complete data (e.g., Kim & Yoon, 2014; Yoon & Millsap, 2007; Jung & Yoon, 2016; Shi, Song & Lewis, 2017a), to the best of our knowledge, no study on SBSS_LMFI so far has considered the issue of missing data. As mentioned above, two methods can be used to deal with ordinal missing data in SBSS_LMFI. These methods are described in detail below along with their strengths and limitations.

Robust full information maximum likelihood (rFIML)

rFIML is an extension of FIML to account for continuous data with non-normal distributions. To explain how rFIML works, we start with the log-likelihood function for FIML. FIML accounts for missing data by creating case-wise log-likelihood functions according to missing data patterns, allowing it to efficiently use all available information in the dataset to estimate model parameters.

The log-likelihood function used in FIML for case i is written as

$$ {l}_i\left(\theta \right)={K}_i-\frac{1}{2}\log \left|\varSigma {\left(\theta \right)}_i\right|-\frac{1}{2}{\left({x}_i-{\mu}_i\right)}^{\prime}\varSigma {\left(\theta \right)}_i^{-1}\left({x}_i-{\mu}_i\right), $$
(1)

where Ki is a constant. Σi, μi, and xiare the model implied covariance matrix, mean vector, and the observed data for case i, respectively. The individual likelihoods are summed to form the sample log-likelihood function (Arbuckle, 1996, p248; Yuan & Bentler, 2000, p.167–168):

$$ l\left(\theta \right)=\sum \limits_{i=1}^N{l}_i\left(\theta \right). $$
(2)

The test statistic of the model can be then calculated as follows, and assumed to follow a Chi-square distribution.

$$ {T}_{FIML}=-2\left(l\left(\hat{\theta}\right)-l\left(\hat{\beta}\right)\right), $$
(3)

where \( l\left(\hat{\theta}\right) \) and \( l\left(\hat{\beta}\right) \) are maximized log likelihoods under the tested and saturated models, respectively (Yuan & Bentler, 2000).

Past research has shown that FIML produces more accurate parameter estimates and χ2 test statistics than traditional missing data methods such as listwise or pairwise deletion (PD) (Enders & Bandalos, 2001). Effectively recovering missing information often requires integrating auxiliary variables (the variables that predict missingness but are not part of the tested model) into the missing data handling process for CFA models. This can be done with FIML using Graham’s saturated model method by allowing the correlations between auxiliary variables and residuals of manifest indicators to be freely estimated (Graham, 2003).

However, FIML assumes multivariate normality, which is often violated in practice and lead to biased test statistics. To solve the problem, rFIML corrects the test statistic by multiplying the test statistic in Eq. (3) by a correction factor c as follows.

$$ {T}_{rFIML}=c\times {T}_{FIML}. $$
(4)

Detailed information on how c is calculated can be found in Yuan and Bentler (2000). Since MFI is also assumed to follow a Chi-square test distribution, it can be corrected in a similar fashion when rFIML is used (see Muthén, 2011, Jul, 26).

As a direct extension of FIML, rFIML inherits the capability of FIML to handle missing data in the estimation process while accounting for nonnormality. However, rFIML still treated ordinal data as continuous. Past research has shown that this could result in distorted test statistics, although the bias may be ignorable when the number of categories within an item is no less than five (e.g., Rhemtulla, Brosseau-Liard, & Savalei, 2012).

WLSMV with pairwise deletion (WLSMV_PD)

Unlike rFIML, WLSMV is an ordinal estimator extended from the weighted least squares (WLS) estimation method. WLS assumes that for each ordinal indicator yj with C categories, there is a normal distributed latent response variable (\( {y}_j^{\ast } \)) underlying it. This latent response variable is categorized into C categories using C-1 thresholds (τj, 1,τj, 2,. …τj, c − 1) such as

$$ {y}_j=\left\{\begin{array}{c}1\\ {}2\\ {}\vdots \\ {}C-1\\ {}C\end{array}\begin{array}{c}\\ {}\\ {}\\ {}\\ {}\end{array}\begin{array}{c} if\\ {} if\\ {}\vdots \\ {} if\\ {} if\end{array}\begin{array}{c}\\ {}\\ {}\\ {}\\ {}\end{array}\begin{array}{c}{y}_j^{\ast}\le {\tau}_{j,1}\\ {}{\tau}_{j,1}\le {y}_j^{\ast}\le {\tau}_{j,2}\\ {}\vdots \\ {}{\tau}_{j,c-2}<{y}_j^{\ast}\le {\tau}_{j,c-1}\\ {}{\tau}_{j,c-1}<{y}_j^{\ast}\end{array}\right\}. $$
(5)

The thresholds and other parameters in the model (e.g., loadings) are typically estimated via a three-stage process (e.g., Muthén, 1984; Muthén, De Toit & Spisic, 1997; Wirth & Edwards, 2007). First, the sample thresholds for each indicator are estimated using univariate information. Second, the polychoric correlation between each pair of ordinal indicators is estimated by treating the sample thresholds estimated in the previous step as fixed (Olsson, 1979 and Bollen, 1989, p.439–443). Third, the sample thresholds and polychoric correlations obtained in steps 1 and 2 are used to form a discrepancy function, which is minimized to obtain the estimates for the model parameters (\( \hat{\theta} \)). The discrepancy function WLS can be written as

$$ {\mathrm{F}}_{\mathrm{WLS}}={\left(s-\sigma \left(\theta \right)\right)}^{\prime }{W}^{-1}\left(s-\sigma \left(\theta \right)\right), $$
(6)

where s is a vector of sample thresholds and polychoric correlations (unique elements in the sample polychoric correlation matrix), θis a vector of model-implied thresholds and polychoric correlations; W is the weight matrix, which is usually a consistent estimate of the covariance matrix of s. The test statistic can be then calculated as

$$ {T}_{WLS}=\left(N-1\right)\times {F}_{WLS}\left(\hat{\theta}\right), df=p\ast \hbox{--} q, $$
(7)

where \( {F}_{WLS}\left(\hat{\boldsymbol{\uptheta}}\right) \) is the minimized discrepancy function, N is the sample size, p* is the number of unique elements in s, and q is the number of parameters in the model.

TWLS asymptotically follows a χ2 distribution, though simulation studies show that it requires a very large sample size, which is often impractical for most research in social and behavioral sciences (e.g., Flora & Curran, 2004). A solution to this problem is to use only the diagonal elements of the weight matrix in Eq. (6) in the discrepancy function as shown below

$$ {\mathrm{F}}_{DWLS}={\left(s-\sigma \left(\theta \right)\right)}^{\prime }{W_D}^{-1}\left(s-\sigma \left(\theta \right)\right), $$
(8)

whereWD is a matrix with all the off-diagonal elements in W fixed to 0s. This approach is known as diagonally weighted least squares estimation (DWLS) (Muthén, et al., 1997; Wirth & Edwards, 2007).

The information loss caused by diagonalizing the weight matrix could distort the test statistic (Savalei, 2014). WLSMV provides a correction to DWLS for the information loss so that the mean and variance of the test statistic will approximate a χ2 distribution (DiStefano & Morgan, 2014; Muthén, et al., 1997). Previous research found that WLMSV outperformed other correction methods (DiStefano & Morgan, 2014). Thus, we considered only WLMSV in the current study.

For complete ordinal data, WLSMV appears to outperform rFIML. It provides more accurate test statistics (Li, 2016) and valid MFI (Yoon & Kim, 2014). However, WLMSV has its limitations when missing data present (Muthén, Muthén & Asparouhov, 2015). As mentioned earlier, WLSMV is a multi-stage process that uses only univariate and bivariate information in the first two stages. This makes WLSMV a limited information method instead of a full information estimator. Consequently, it cannot incorporate missing data patterns into its discrepancy function and relies on other methods to deal with missing data. In practice, PD has often been coupled with WLSMV for dealing with missing data (e.g., Chan, Gerhardt & Feng, 2019; Erreygers, Vandebosch, Vranjes, Baillien, & De Witte, 2018; Hakkarainen, Holopainen, & Savolainen, 2016; Kim, Wang & Sellbom, 2018; Willoughby, Pek, Greenberg & Family Life Project Investigators, 2012). In the current study, we refer to this combination as WLSMV_PD.

PD is not an ideal missing data technique. Past research found that PD could substantially inflate the type I error rates of χ2 tests in SEM with continuous data (e.g., Enders & Bandalos, 2001; Savalei & Bentler, 2005). A better method for dealing with missing data with WLSMV is multiple imputation (Asparouhov, & Muthén, 2010; Teman, 2012). For example, Asparouhov & Muthén, (2010) found that WLSMV combined with multiple imputation would provide more accurate point estimates than WLSMV_PD. Nevertheless, we did not consider multiple imputation in the current study because so far, there is no good way to pool MFI and the χ2 test statistic across imputations with WLSMV (Liu et al., 2017; Muthén, 2017).

Purpose of the current research

As described above, rFIML and WLSMV_PD both have their own strengths and limitations. rFIML is good at handling missing data, but it assumes that ordinal data are continuous. In contrast, WLSMV_PD is good at handling ordinal data, but it uses a suboptimal method to deal with missing data. To the best of our knowledge, it is still not clear which one will perform better or under what conditions one would be preferred over the other in SBSS. Without such information, researchers have often chosen one of the methods based on personal preference, without solid justifications (e.g., Fokkema, et al., 2013). To fill in this gap in the literature, the current study aims to examine the relative performance of rFIML and WLSMV_PD in SBSS_LMFI with ordinal missing data using Monte Carlo simulation.

Simulation design

Population generation model

Following Jung and Yoon (2016), we used a two-group (groups A and B) single-factor CFA model as the population model. There were six or 12 Likert-type indicators per group, representing smaller or larger models. A population model with six indicators per group is shown in Fig. 1. Group A was used as the reference group, for which all the model parameters were fixed across all conditions. Group B was the focus group, where the model parameters for some indicators were varied across conditions.

Fig. 1.
figure 1

The population model with six indicators. Note: Aux: auxiliary variable. VA: observed indicators ingroup. A. VB: observed indicators ingroup A

Full size image

We created invariant and non-invariant conditions, allowing us to examine both type I and type II error rates associated with the methods. For invariant conditions, all items in groups A and B had factor loadings fixed at 0.7 (Jung & Yoon, 2016; Sass et al., 2014). To create non-invariant conditions, certain values (depend on the pattern of non-invariance) were subtracted from either the loadings or the thresholds of items 2 and 4 in group B for the six indicators per group model. For the 12 indicators per group model, non-invariance occurred on items 2, 4, 6, and 10. The number of non-invariant items is doubled here to maintain the proportion of non-invariant items constant. The residual term of each indicator follows a normal distribution with mean at 0 and variance as 1 – the square of the corresponding loading.

In addition, for both invariant and non-invariant conditions, there were complete data and missing data conditions. For missing data conditions, substantial amounts of missing data were imposed on all non-invariant items (i.e., items 2 and 4 in group B for the smaller model and items 2, 4, 8, and 10 in group B for the larger model). The missingness was determined by an auxiliary continuous variable correlated with the latent factor in group B by r = 0.5. Thus, the generated missing data mechanism was missing at random (MAR). Note that in the missing data conditions, in addition to the MAR data mentioned above, we also imposed 5% missing completely at random (MCAR) data on all items in the model to increase the external validity of our simulations, given that missing data could occur on all items and different missing data mechanisms could coexist in reality. The details of the missing data conditions and missing data generation process are explained below.

Design factors

The design factors we manipulated included (1) Sample size, (2) Model size, (3) Number of categories within each indicator, (4) Distribution of thresholds, (5) Location of non-invariance, (6) Pattern of non-invariance, and (7) Missing data proportion. The first six factors were between-replication factors. The last factor was a within-replication factor.

Sample size

The sample size was varied at three levels: 500 (250 per group), 1000 (500 per group), or 2000 (1000 per group), representing small, medium, or large sample sizes. These settings are identical to those adopted in Jung & Yoon (2016).

Model size

The number of items per group was varied at two levels: six items (a smaller model) per group and 12 items per group (a larger model), referring to previous research on missing data and specification search problems in the framework of MF-CFA (Enders & Gottschall, 2011; Yoon & Millsap, 2007)

Number of categories per item

We varied this factor at two levels: three or five. As mentioned above, past research has recommended using rFIML for ordinal data with ≥ 5 categories; however, it would still be interesting to see how rFIML would perform in relative to WLSMV_PD for ordinal data with less than five categories.

Distribution of thresholds

The distribution of thresholds is varied to be either symmetric or asymmetric. For five-point indicators, (– 1.30, – 0.47, 0.47, 1.30) and (–0.253, 0.385, 0.842, 1.282) are used to represent symmetric and asymmetric thresholds, respectively, following Sass et al. (2014). For three-point indicators, (– 0.83, 0.83) and (– 0.50, 0.76) are used to represent symmetric and asymmetric thresholds, respectively, following Rhemtulla et al. (2012).

Location of non-invariance

Non-invariance was placed on either the loadings or thresholds of non-invariant items (i.e., items 2 and 4 for the smaller model and items 2, 4, 8, and 10 for the larger model). For convenience, we refer to the two types of conditions as loading and threshold non-invariant conditions, respectively.

Pattern of non-invariance

In the non-invariant conditions, the loadings or thresholds of non-invariant items were subtracted by certain values (depending on the pattern of non-invariance). We created four patterns of non-invariance: uniform (small, large, and mixed) and non-uniform (Jung & Yoon, 2016; Meade & Bauer, 2007). For uniform patterns, the directions of non-invariance were consistent across non-invariant items. Specifically, the loadings or thresholds of non-invariant items in group B were subtracted by (0.2, 0.2), (0.4, 0.4), or (0.3, 0.5) in conditions for the smaller model and by (0.2, 0.2, 0.2, 0.2), (0.4, 0.4, 0.4, 0.4), or (0.3, 0.5, 0.3, 0.5) in conditions for the larger model to create small, large, or mixed non-invariant conditions (see also Jung & Yoon, 2016).

For non-uniform non-invariance, the directions of non-invariance were different across the items. Specifically, the loadings or thresholds of non-invariant items in group B were subtracted by (0.2, – 0.2) in conditions for the smaller model and by (0.2, – 0.2, 0.2, – 0.2) in conditions for the larger model. Model parameters for these patterns of non-invariance for five-point indicators are presented in Table 1. Those for three-point indicators can be found in the supplementary material. We also quantified the magnitude (i.e., effect size) of non-invariance for each of these patterns using the dmacs statistics proposed by Nye & Drasgow (2011). Given the space limit, these effect sizes along with their interpretation guidelines provided by Nye, Bradburn, Olenick, Bialko & Drasgow (2019) can be also found in supplementary materials.

Table 1. Model parameters of different patterns of non-invariance with five-point indicators
Full size table

Missing data proportion

We imposed MAR missing data on non-invariant items in group B. We varied the MAR data rate at three levels: 0% (no missing data), 30% MAR (medium) and 50% MAR (large). Similar to Wu, Jia and Enders (2015), the missingness on these items was determined by the auxiliary variable (see Fig. 1), such as that participants with higher scores on the auxiliary variable in focal group were more likely to have missing data. Specifically, three steps are involved. First, auxiliary variable values in focal group were rank ordered. Second, the probabilities of having missing data on items 2 and 4 for the smaller model and on items 2, 4, 8, and 10 for the larger model for each individual were then calculated as 1 − ranki/nb. Here ranki is the rank order of the auxiliary variable score for individual i andnbis the sample size of group B. Third, for each participant and incomplete item, a random number u was generated from a uniform distribution. If u was less than the probability, then the data point was missing. This procedure was repeated for non-invariant items until the desired MAR data rate (30% or 50%) was reached for each item. As mentioned above, in addition to the MAR data, we added 5% MCAR data to all items in both groups in the missing data conditions.

In sum, there are 240 between-replication conditions in total. Among them, there are 192 non-invariant conditions: sample sizes (3) × model sizes (2) × number of categories per item (2) × distribution of thresholds (2) × locations of non-invariance (2) × patterns of the non-invariance (4). There are 48 invariant conditions: sample size (3) × model sizes (2) × number of categories per item (2) × distribution of thresholds (2) × loading or threshold invariance (2). Note that the terms “loading” or “thresholds” in the invariant conditions only represent the target parameters of the search. All parameters (loadings and thresholds) are invariant in the invariant conditions. There are 500 replications for each condition. All datasets were generated using R 3.3.1 (R core team, 2016).

Implementation of the methods

For each replication, we conducted SBSS_LMFI using rFIML and WLSMV_PD (Muthén & Muthén, 1998–2017). The auxiliary variable was included in both groups using the saturated correlation model proposed by Graham (2003). In SBSS_LMFI, we used 3.841 as the cutoff for a significant MFI. Following Yoon & Kim (2014), the search procedure continues until there is no significant MFI in the model on target parameters or until the global χ2 test became non-significant (p > 0.05). We used the loading and intercept (first threshold) of item 1 as the anchor parameters; they were always constrained to be equal across groups thus were not included in the search. For WLSMV_PD, the model was specified using delta parameterization. Details about this parameterization can be found in Muthén and Asparouhov (2002). Given that WLSMV_PD estimates thresholds and there are multiple thresholds in an ordinal indicator, the specification search of WLSMV_PD involves more steps than rFIML n the thresholds non-invariant conditions (note: rFIML only search one intercept per item in the threshold non-invariant conditions).

Outcomes

We evaluated the two methods using three outcome variables that have been considered in past research (Jung & Yoon, 2016; Yoon & Kim, 2014; Yoon & Millsap, 2007): model level type I and type II error rates, and perfect recovery rates. The model level type I error rate is the probability of misidentifying any invariant parameters as non-invariant across all replications of a condition; the model level type II error rate is the probability of misidentifying any non-invariant parameters as invariant across all replications of a condition. The perfect recovery rate is defined as the probability of correctly identifying all non-invariant and invariant parameters in all items across all replications of a condition.

Note that with the definitions, model level type I errors and type II errors could appear in a partial invariance model in non-invariance conditions simultaneously. In contrast, the perfect recovery rate is considered as a criterion that is similar to but more rigorous than power (Jung & Yoon, 2016), as it is a function of both type I and type II error rates. A perfect recovery can be achieved only when neither type I nor type II errors occurred. For invariant conditions, only model level type I errors could occur and the perfect recovery rates would be equal to 1 – model level type I error rates. Thus, we only calculated and reported model level type I errors for invariant conditions.

Results

All specification searches conducted using rFIML converged. About 0.3% of the replications had convergence problems with WLSMV_PD. Most of these non-convergent replications occurred with the larger models, especially in loading non-invariance conditions where at least one loading in the model was lower than 0.4 with small sample sizes. These replications were excluded from the rest of the analyses.

Because five-point Likert scales are much more popular than three-point Likert scales, we present the results for five-point indicators first and then show how the results for three-point indicators were similar or different. In addition, given relative performances between methods are similar and consistent between conditions with six item per group model and the conditions with the 12 item per group models, we thus focused on describing the results for the smaller model.

The results for five-point indicators

Model level type I error rates and perfect recovery rates for invariant conditions

The result for the model level type I error rates is shown in Table 2. The type I error rates above 0.1 are highlighted. When data were complete, both methods maintained the type I error rate around or below the nominal level (0.05). However, when data were missing, rFIML substantially outperformed the WLSMV_PD in controlling type I error rates. The type I error rates from rFIML were below or around .05 across all missing data conditions. In contrast, WLSMV_PD yielded inflated type I error rates, particularly in the conditions with large sample sizes and high missing data rates. For example, in the conditions where the sample size was 2000 and the missing data rate was 50%, the type I error rates from WLSMV_PD were inflated up to 0.40 and 0.98 for the metric and scalar invariance models, respectively. As mentioned above, for non-invariant conditions, perfect recovery rates are equal to 1 minus type I error rates, thus lower type I error rates can be directly translated to higher perfect recovery rates.

Table 2 Model level type I error rates in invariance conditions with five-point indicators
Full size table

Perfect recovery rates for non-invariant conditions

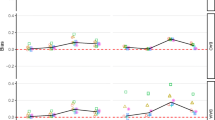
The perfect recovery rates of conditions with five-point indicators are presented in Figs. 2, 3, 4, and 5. As shown in these figures, the results from both methods shared the following patterns: (a) As sample size increased, the perfect recovery rate also increased; (b) As missing data rate increased, the perfect recovery rate decreased in most conditions; (c) As model size increased, the perfect recovery rate decreased; (d) Neither of the methods had sufficient perfect recovery rates (> 0.8) when sample size was smaller than 1000, regardless of the patterns of non-invariance. In addition, as the thresholds changed from symmetric to asymmetric, the perfect recovery rate tended to slightly decrease. The detailed values of the perfect recovery rates in the conditions can be found in supplementary materials.

Fig. 2
figure 2

Perfect recovery rates of the methods in loading non-invariance conditions with five-point symmetric indicators

Full size image
Fig. 3
figure 3

Perfect recovery rates of the methods in thresholds non-invariance conditions with five-point symmetric indicators

Full size image
Fig. 4
figure 4

Perfect recovery rates of the methods in loading non-invariance conditions with five-point asymmetric indicators

Full size image
Fig. 5
figure 5

Perfect recovery rates of the methods in thresholds non-invariance conditions with five-point asymmetric indicators

Full size image

The perfect recovery rates were more comparable between rFIML and WLSMV_PD under complete data conditions. The performance of the two methods diverged with the presence of missing data. Specifically, perfect recovery rates of rFIML were more consistent across design factors and tended to decrease as missing data rates increased across conditions. Factors such as patterns of non-invariance appeared to have more profound and complex impacts on WLSMV_PD when missing data present. In most conditions with uniform non-invariance (i.e., the non-invariance of items followed the same direction), the perfect recovery rates from WLSMV_PD only slightly decreased as the missing data rate increased and in general were higher than those from rFIML. In contrast, for non-uniform non-invariance conditions, the perfect recovery rates from WLSMV_PD substantively decreased as the missing data rate increased and were lower than those from rFIML.

In addition to the pattern of non-invariance, the relative performance between rFIML and WLSMV_PD was also affected by the location of non-invariance and threshold asymmetry. Specifically, when non-invariance occurred in loadings of indicators with asymmetric thresholds (see Fig. 4), rFIML outperformed WLSMV_PD in perfect recovery rate even under uniform non-invariance conditions.

Model level type I and type II error rates for non-invariant conditions

The type I error rates for the loading non-invariant conditions for the smaller model are shown in Table 3. As shown in the table, rFIML provided a good control of the type I error rate across all conditions. In contrast, WLSMV_PD yielded inflated model level type I error rates and the type I error rates increased as the missing data rate increased.

Table 3 Model level type I error rates in loading non-invariance conditions with six five-point indicators per group
Full size table

Tables 4 and 5 display the type II error rates for the smaller model . The type II error rates higher than 0.2 are highlighted in these tables. The type II error rates of rFIML generally increased as the missing data rate increased with only a few exceptions. Both methods had type II error rates lower than 0.2 when thresholds were symmetric, magnitude of non-invariance and sample size were large.

Table 4 Model level type II error rates in loading non-invariance conditions with six five-point indicators per group
Full size table
Table 5 Model level type II error rates in threshold non-invariance conditions with six five-point indicators per group
Full size table

Comparing the two methods, rFIML tended to have lower model level type II error rates than WLSMV_PD under non-uniform non-invariance conditions, particularly with the presence of missing data. In contrast, for uniform non-invariance, WLSMV_PD outperformed rFIML, except when non-invariance occurred in loadings and thresholds were asymmetric.

The results for three-point indicators

The results from the three-point indicators were mostly consistent with those from the five-point indicators. For instance, rFIML continued outperforming WLSMV_PD in controlling the model level type I error rates (see Table 6). For perfect recovery rates, similar patterns were observed between the results for the three-point and five-point indicators (see Fig. 6), although the perfect recovery rates of rFIML under the three-point indicators were lower than those from the five-point indicators by comparing Fig. 6 to Fig. 2. In general, rFIML outperformed WLSMV_PD under non-uniform non-invariance or when non-invariance occurred in loadings and thresholds were asymmetric. WLMSV_PD, on the other hand, outperformed rFIML under uniform non-invariance.

Table 6 Model level type I error rates in invariance conditions with three-point indicators
Full size table
Fig. 6
figure 6

Perfect recovery rates of the methods in loading non-invariance conditions with six symmetric three-point indicators per group in the model

Full size image

There is one difference, however, between the two types of indicators. This difference is shown in the upper panel of Fig. 7. It appeared that with three-point indicators, WLSMV_PD could outperform rFIML under non-uniform non-invariance when the non-invariance occurred in the thresholds and there was a larger number of asymmetric items (i.e., 12 items per group) in the model.

Fig. 7
figure 7

Perfect recovery rates of the methods in thresholds non-invariance conditions with 12 asymmetric three-point indicators per group in the model

Full size image

Conclusions and discussion

Specification search is an important follow-up procedure in ME/I when full invariance models cannot be achieved (Putnick, & Bornstein, 2016). Focusing on backward specification search, we evaluated the performance of two commonly used methods, rFIML and WLSMV_PD, by examining their model-level type I rates, type II error rates, and perfect recovery rates in the current study. The major findings are summarized and discussed below.

Major findings

First, in both invariant and non-invariant conditions, we consistently found that rFIML provided a better control of model-level type I error rates than WLSMV_PD across all the conditions when missing data present, including those with three-point indicators. This suggests that the advantage of WLSMV_ PD in dealing with the ordinal nature of the data is comprised by its use of PD. At least two aspects of WLSMV_PD could contribute to the inflated type I error rates. First, it treats the sample thresholds and polychoric correlations as if they were obtained from complete data, thus fails to account for the uncertainty due to missing data in estimating these parameters. Second, depending on missing data patterns, the thresholds and polychoric correlations are likely calculated using different sample sizes, which could distort the globalχ2 statistics (Bollen, 1989). Since MFI is a χ2 statistic, this could also bias MFI.

Second, in non-invariance conditions, we found that decrease in sample size, increase in missing data rate, and decrease in the amount of non-invariance were generally associated with lower perfect recovery rates for both methods. When sample size was small, neither method produced > .8 perfect recovery rates in most conditions. In addition, increase in model size and asymmetry of thresholds could also decrease perfect recovery rates. These results are consistent with the findings from previous research based on complete data. For example, Yoon & Millsap (2007) found that increase the model size decreased the perfect recovery rates of SBSS_LMF. Sass et al. (2014) found that asymmetric thresholds lowered the power of Δχ2 tests between invariance models for robust maximum likelihood (ML) estimator in all conditions and WLSMV in most conditions.

Third, WLSMV_PD produced higher perfect recovery rates than rFIML in uniform non-invariance conditions. However, this may be due to the fact that WLSMV_PD had inflated power to detect uniform non-invariance given its inflated type I error rates. Thus, researchers need to be cautious about using WLSMV_PD even under uniform non-invariance. rFIML had lower power to detect uniform non-invariance. One possible explanation is that continuous estimators are in general less sensitive to item level features of ordinal indicators (Oort, 1998). Therefore rFIML requires a larger sample to precisely detect differences between ordinal items. This could also explain why the type I error rates from rFIML were conservative. Similar findings have been reported in previous research (e.g., Chen et al., 2019).

Fourth, rFIML showed higher perfect recovery rates and power than WLSMV_PD in detecting non-uniform non-invariance (i.e., directions of non-invariance are different across non-invariant items) when missing data present. Similar findings have been obtained in previous research using complete continuous data. For example, Meade and Lautenschlager (2004) and Whittaker and Khojasteh (2013) found that the ML estimator for complete data had higher power to detect non-uniform non-invariance than uniform non-invariance. They believed that this had to do with communalities of non-invariance items (Whittaker & Khojasteh, 2013). Given how non-invariance was simulated in those studies (e.g., higher loadings), non-uniform non-invariance may have created a scenario where the non-invariant item(s) had a higher communality for the focal group, increasing the influence of these non-invariant items and consequently the power of rFIML. Higher power combined with lower type I error rates resulted in higher perfect recovery rates of rFIML.

These non-invariant items with high communalities, however, did not benefit but actually harm the performance of WLSMV_PD, because impacts of missing data were magnified by PD in this scenario. A similar result was reported in Enders and Bandalos (2001) which showed that when missing data in SEM were handled using PD, indicators with higher communalities demonstrated more biased loading estimates. This could explain why perfect recovery rates of WLSMV_PD were much lower than rFIML under non-uniform non-invariance.

Other findings and issues

In addition to the general patterns described above, we found two interesting exceptions. First, in the threshold non-uniform non-invariance conditions, rFIML produced lower perfect recovery rates when there were only three categories per indicator, the model size was large, and thresholds were asymmetric. This implies that even with non-uniform non-invariance, there may be a tipping point where the advantage of rFIML in dealing with missing data would be outweighed by its disadvantage of dealing with the discrete nature of the ordinal data if the data are highly discrete and asymmetric.

Second, despite the general advantages of WLSMV_PD over rFIML in uniform non-invariance conditions, we found that if non-invariance appeared in loadings of items with asymmetric thresholds, WLSMV_PD was inferior to rFIML regardless of the non-invariance pattern. Similar findings were reported in Yoon & Kim (2014). This implies that WLSMV_PD may have more difficulty than rFIML in separating the source of non-invariance from the asymmetry of thresholds.

Practical recommendations

As we expected, neither of the methods is perfect. Thus, there is no one-size-fits-all recommendations, and preference for a method should be determined based on which criterion is deemed most important as well as characteristics of the data such as the pattern of non-invariance. Because type I errors are generally viewed as more harmful than type II errors, it is often more important to control type I error rates than minimize type II error rates. Thus, if controlling type I error rates is the priority, rFIML is generally preferred to WLSMV_PD. Using rFIML will not only ensure a good control of model level type I error rates but also provide higher power to detect non-invariant items if the pattern of non-invariance is non-uniform, unless there are less than five categories, the model size is large, and thresholds are asymmetric. On the other hand, if maximizing the perfect recovery rate is the goal, then WLSMV_PD appears to be more favorable when non-invariance is uniform. Otherwise, rFIML is still preferred. One downside of using rFIML is that it will have lower power to detect uniform non-invariant items than WLSMV_PD when thresholds are symmetric. According to our study, rFIML seemed to require at least 1000 and 2000 participants to demonstrate sufficient perfect recovery rates in conditions with five-point indicators and three-point indicators, respectively. These sample sizes could be unrealistic for some studies.

In addition to the above recommendations, we want to emphasize the importance of theory when using MFI to build partial invariance models. Many researchers have cautioned that using MFI as a purely data-driven, post hoc model modification index could lead to misleading results (e.g., MacCallum, Roznowski, & Necowitz, 1992; Yoon & Millsap, 2007). Thus, theoretical justification and cross-validation for invariance model modifications are important issues that should be considered during the search process (Byrne et al., 1989; Yoon & Millsap, 2007).

Limitation and future directions

As in many simulation studies, we could not include all conditions and methods of interest in the current study. First, we assume that the anchor item is correctly specified, which may not always be the case in practice. Yoon & Millsap (2007) demonstrated that incorrect anchor variables could make invariance items appear to be non-invariant. Johnson, Meade & DuVernet (2009) also found that using wrong anchor items could substantively affect item level ME/I tests and make group comparisons unreliable. Although several methods to select anchor items have been proposed (e.g., Jung & Yoon, 2017), they have not been examined with missing data. Thus, this is a potential avenue for future research.

Second, as in most specification search research, we assumed that the latent factors in both groups were normally distributed. However, researchers have found that non-normal latent variables could affect the performance of WLSMV and the robust ML estimator for complete data (Savalei & Folk, 2014; Suh, 2015). It would be interesting to examine the joint effect of non-normal latent factors and ordinal missing data on the performance of the two approaches considered in our study.

Third, we only examined one of the search processes, SBSS_LMFI, because of its popularity in both methodological and empirical literature. However, SBSS_LMFI has its limitations. One main limitation is that it may not perform well when the percentage of non-invariance items was high (e.g., 2/3 of the items are non-invariant) (Yoon & Millsap, 2007). In this case, the restricted model used in the beginning of a backward search process (e.g., full-scale invariance model) would be severely misspecified (i.e., too many inappropriate equality constraints), leading to biased results (Yoon & Millsap, 2007).

This problem can be mitigated by using forward specification search methods because they start with a less restricted invariance model. Recently, Jung and Yoon (2016) proposed a forward specification search process that utilizes the CIs of differences between corresponding parameters across groups (e.g., loading differences of corresponding items in a configural invariance model). Using complete continuous data, they demonstrated that their method was at least as good as or even slightly better than SBSS_LMFI. We did not include this approach in our study for two reasons: (1) this approach has not been widely adopted by empirical researchers, and (2) It had very similar performance to SBSS_LMFI in simulations (see Jung & Yoon, 2016).

Several other advances in specification search would also deserve researchers’ attention. There are specification methods developed based on penalized ML estimators (e.g., Belzak, & Bauer, 2020; Huang, 2018; Jacobucci, Grimm, & McArdle, 2016; Liang, & Jacobucci, 2019). Emerging evidence showed that these methods could provide a better control on type I error rates than traditional methods such as item response theory (e.g., Belzak, & Bauer, 2020). In addition, with some recently developed software, researchers could use two-stage FIML to handle missing data problems with penalized ML estimators in a framework of multiple group analyses (e.g., the lslx package in R , Huang, 2020). There are also specification search methods developed using Bayesian approaches. For instance, Shi, Song, Liao, et al., (2017b) showed the possibility of using Bayesian SEM to preform forward specification search with complete continuous data. Given that Bayesian estimators are capable of handling ordinal missing data and advantageous in dealing with small sample sizes (e.g., Muthén, et al., 2015; McNeish, 2016), we believe that Bayesian SEM is a promising method to solve the limitations shared by the frequentist approaches. These new methods certainly warrant further research under ordinal missing data.