One of the most important concepts in the field of numerical cognition is the “number sense,” an innate and evolutionary grounded ability that allows humans and other species to understand and manipulate numerical quantities (Dehaene, 1997). This unique ability is thought to be rooted in the approximate number system (ANS), a nonverbal mechanism for estimating the number of elements included in a visual stimulus, which maps numerosities using compressed and partially overlapping analog representations (Piazza, 2010). The ANS acuity is usually assessed by using arrays of elements (often dots with different size) as nonsymbolic number stimuli. Three tasks are mainly used to investigate the ANS: In the estimation task (Fig. 1A), participants are asked to judge the numerosity of an array (e.g., Izard & Dehaene, 2008); in comparison tasks, they are presented with two arrays and have to choose the most numerous (Fig. 1B; e.g., Gebuis & Reynvoet, 2012a); in the habituation paradigm, they look passively at a series of briefly presented arrays (e.g., Xu & Spelke, 2000). Additionally, the match-to-sample task, originally created for studying short-term memory, can be adapted for studying numerical cognition: in this task, participants are presented with a sample array and they have to identify a matching stimulus among a group of comparison arrays (e.g., Diester & Nieder, 2007).

Fig. 1
figure 1

Examples of an estimation task (A) and a comparison task (B). In the former, the participant has to estimate the number of elements in the array; in the latter, the participant has to choose the more numerous of the two arrays

Full size image

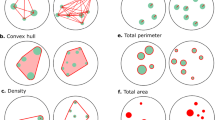
A constitutive element of the stimuli used in these tasks is represented by the non-numerical, continuous properties belonging to the visual domain. These visual features are (1) average diameter, a measure of the dimension of the single elements of the stimulus (directly correlated with average surface and average contour; (2) total contour, or the sum of the perimeters of all the elements (Fig. 2A); (3) total surface, or the sum of the surfaces of all the elements (Fig. 2B); (4) convex hull, the surface subtended by a hypothetical lace encircling all the external elements (Fig. 2C); and (5) density, a measure of the distance between the elements, usually calculated with the formula total surface divided by convex hull (although such a formula might be inaccurate under some circumstances; see the Method section).

Fig. 2
figure 2

Demonstration of the nonnumerical, continuous properties (colored in red) of nonsymbolic number stimuli (visual features): total contour (A), total surface (B), and perimeter of the convex hull (C)

Full size image

In a natural environment, numerosity typically covaries with the visual features of the stimuli: five apples differ from ten apples not only in numerosity, but also in amount of volume, density, surface; likewise, in an experimental setting, equating all the visual features of stimuli with different numerosities is geometrically impossible (Salti, Katzin, Katzin, Leibovich, & Henik, 2017). It is therefore mandatory to rule out the possibility that participants might use visual features instead of numerosity as a strategic shortcut to solve the task: The rationale is that—by controlling the stimuli in a way that discourages participants from relying on visual features, forcing them to judge the numerosity of stimuli—it is possible to obtain a “pure” measure of the ANS (Piazza, Izard, Pinel, Le Bihan, & Dehaene, 2004). To this aim, stimuli are often implemented in a way that disrupts the correlation between visual features and numerosity at a set level (Izard & Dehaene, 2008; Libertus, Odic, & Halberda, 2012; Piazza et al., 2004). These studies took for granted that the visual features of the stimuli were properly controlled for, thereby pushing the authors to interpret their results from a pure “number sense” perspective. Indeed, one distinctive trait of the ANS resides in the normalization procedure of the visual features, which should enable participants to process numerosity without any bias. According to this view, the ANS is supposed to allow humans and other species to estimate the numerosity of sets of elements, regardless of the visual features of the stimuli (Dehaene, 1997). However, after the development of an algorithm capable of manipulating the visual features of the stimuli more accurately (Gebuis & Reynvoet, 2011), this core tenet of ANS theory has been strongly criticized. Several studies have argued that visual features still bias the numerosity judgment, even when numerosity and visual features are not correlated across the set of stimuli: for instance, stimuli with low average diameter, total surface and density and large convex hull are consistently overestimated in an estimation task (Gebuis & Reynvoet, 2012b). These controversial results elicited the birth of two alternative theories: One theory invokes the presence of a sensory integration system, exclusively based on the processing of visual features, making the ANS unnecessary (Gebuis, Cohen Kadosh, & Gevers, 2016), and another endorses a conceptual shift from a specific sense of number to a broader sense of magnitude (Leibovich, Katzin, Harel, & Henik, 2017b). This increased awareness on how visual features impact behavioral performance triggered important methodological improvements in a wide range of perspectives, such as the creation of more approaches for generating nonsymbolic stimuli in a more controlled way. Gebuis and Reynvoet (2012a) modified their original algorithm (Gebuis & Reynvoet, 2011), introducing the concept of congruency in the comparison task. At the same numerical ratio of two stimuli, accuracy is higher when the most numerous stimulus has a larger amount of visual features (congruent condition) with respect to the opposite (incongruent condition). DeWind, Adams, Platt, and Brannon (2015) designed an algorithm to create stimuli with specific number, size, and spacing; using a stimulus set created with such algorithm, they evaluated the effects of the visual features and discerned their impact from that of numerosity, in an attempt to reestablish the soundness of ANS theory. Salti et al. (2017) implemented an algorithm to produce pairs of stimuli equated for the ratio of both a target visual feature and numerosity. Using this method, the authors demonstrated that visual features affect performance in a comparison task even in the subitizing range, although they do not always overpower numerosity: When the ratio of numerosity and visual features across the stimuli was equated, their impact on performance was basically the same.

It appears clear that the aforementioned algorithms are meant to be powerful instruments for exploring numerical cognition; nevertheless, we recognize that there is still room for methodological improvement. First, there is no agreement about how to measure or control the visual features of the stimuli; in particular, the most complex visual features, such as convex hull and density, are ill-defined, and their manipulation could be improved. Furthermore, the current methods need to be modified whenever they have to meet heterogeneous demands: for instance, if different sets have to be reconstructed for comparative purposes, an exact replication of them can be extremely challenging. Finally, although comparison tasks are among the most useful paradigms for assessing participants’ ability to perceive numerosity, we believe that the estimation task might provide information that cannot be gathered with comparison tasks; nevertheless, no available algorithm is able to readily generate stimuli for both tasks.

Thus, we propose CUSTOM, a new algorithm for generating nonsymbolic number stimuli that offers several main advantages: (a) customization—the new algorithm does not include fixed parameters or rules (aside from the constraints of geometry), thereby providing total freedom to the user in manipulatingthe visual features of the stimuli; (b) precision—the level of control over the visual features of the stimuli created with the new algorithm is more stringent and precise with respect to any other method available; (c) standardization—our algorithm does not need to be modified in order to accomplish different types of manipulation, and having a unique tool capable of replicating previous sets and implementing new ones could facilitate communication in the field, through the use of common measurement units and parameters; and (d) a multipurpose nature—the new algorithm is potentially capable of reproducing the characteristics of any set of stimuli described in an experiment on numerical cognition conducted so far, and it is able to generate stimuli for comparison, estimation, habituation and match-to-sample tasks. In the forthcoming sections we described the core structure of the algorithm and we substantiated our assertions by showing the results obtained from the generation of two sets of visual arrays with different numerosities. The CUSTOM algorithm could represent an asset in the field of numerical cognition, as a versatile instrument for effectively generating high precision visual stimuli within an unbiased theoretical framework.

Method

The CUSTOM algorithm for generating nonsymbolic number stimuli has been implemented as a Matlab (Matlab R2018b, The MathWorks Inc., Natick, Massachusetts, USA) function. The code (together with the scripts, examples and instructions) can be freely downloaded at: https://ch.mathworks.com/matlabcentral/fileexchange/72471-custom-algorithm. The user can insert (as input arguments) a set of parameters representing the following visual features: (a) diameter of dots, (b) total surface, (c) total contour, and (d) convex hull. In the generation of each stimulus, the algorithm includes two core steps: (1) the sizing phase, in which the dot sizes are calculated according to either visual feature a, b, or c above; and (2) the placing phase, in which the dots are first arranged in a random fashion inside an area, and then their position is iteratively adjusted in order to match the desired convex hull value. The randomness introduced in the algorithm implicates that all the images generated with the same input parameters will have exactly the same visual features, although being visually different from each other. Two distinctive qualities in the process of generating the stimuli are worth mentioning: (1) All the visual features are calculated in absolute terms, and (2) the only constraints embodied in the algorithm have a purely geometrical nature. Both of these points indicate that the algorithm is completely unbound by any specific experimental design or theory.

The algorithm is able to discard all the stimuli that do not respect the desired values and those flawed by imperfections, such as those with overlapping dots. For each stimulus successfully created, the information about its parameters (e.g., convex hull, total surface) is stored into a .csv info file. The algorithm is able to generate stimuli with at least two dots and it has been extensively tested up to a numerosity of around 200 elements, although no specific constraints prevent it from generating even larger numerosities (note that with particularly large numerosities, the time needed to create the stimuli might increase). The elements of the stimuli are circles (i.e., dots); both the color of dots and background can be selected by the user. The size of the stimulus canvas can be also selected by the user (the default is value is a 500×500 pixel square). The sequence of operations performed by the algorithm is described in the following paragraphs.

Sizing phase

The Matlab function starts with three different options that enable to keep constant (regardless of numerosity) one of the following visual features related to the size of the dots: (a) dot diameter, (b) total surface, or (c) total contour. An additional option (d) releases the algorithm from any control related to dot size. Note that, for reasons dictated by geometrical constrains, only one of the three sizing visual features can be manipulated at a time (Salti et al., 2017). This has a profound impact when generating the stimuli. If the diameter is fixed (a), all the dots share the same size in all the images generated, thereby causing an increase of both total surface and total contour as numerosity increases. If total surface is held constant across numerosities (b), total contour will be positively correlated with numerosity; on the other hand, if total contour is held constant across numerosites (c), total surface will be negatively correlated with numerosity. In any case, a constant total surface or total contour will cause a decrease in the average size of the elements as numerosity increases. When selecting option b or c, the user can also choose between having (1) a single diameter shared by all the elements (all the dots are of equal size) or (2) a random variability of diameters within a controlled range (the dots have different sizes). The last option (d) requires selecting the range of minimum and maximum dot size; the function will randomly choose each dot size inside such range, excluding any control over the values of both total surface and total contour.

Placing phase

After the sizing phase, the algorithm randomly starts arranging dots inside an area (the user can select between a square or a circle). If there is no control over convex hull, the coordinates of each point of the perimeter of each dot in external position are used as inputs for the Matlab convhulln method, ensuring a pixel-level measure of the convex hull (see Fig. 2C). After calculation of the convex hull of the stimulus, the procedure is complete. Alternatively, if the user has selected the control over the convex hull, an iterative procedure starts:

  1. Step 1:

    The convex hull is calculated.

  2. Step 2:

    The distance between each dot and the center of mass (i.e., the mean of the coordinates of all the dots) is computed.

  3. Step 3:

    If the current convex hull is larger/smaller than the desired value, all the dots are moved toward/away from the center of mass (along the segments connecting each dot to the center).

Steps 1 to 3 are repeated until the value of the convex hull reaches the expected value.

Two expedients have been used to avoid two shortcomings. First, in order to avoid an excessive crowding/dispersion of dots near/from the center of mass, the amount of displacement is weighted by the distance of dots from the center of mass. The farthest dot from the center will have a weight of 1, the closest dot to the center will have a weight of 0, whereas the other dots will have intermediate values. Thus, at the two extremes the farthest dot will undergo the farthest displacement and the closest dot will remain in the same position, whereas the other intermediate dots will move depending on their relative distance from the center of mass. The second issue concerns the fact that achieving a convex hull exactly identical to the desired value would require an impractically long waiting time; in order to speed up the process, we added a tolerance parameter T. For instance, if the desired value of convex hull is X, the algorithm will accept all the convex hull values falling within the range of X plus or minus (X*T)/2. Even with an extremely low tolerance value (the default is .001, but it can be modified by the user), a tangible speed-up of the algorithm can be appreciated, without any negative effect on its precision. The algorithm produces an equal amount of stimuli with larger and smaller convex hull, so that the mean convex hull of the set will be equal to the desired value.

The high versatility of the algorithm is reflected by the wide range of numerosities that can be handled: even the convex hull of stimuli with only two elements can be controlled (note that the convex hull of a stimulus with a single element is not meaningful because it corresponds to its total surface). For what concerns large numerosities, there is no specific limit.

Generation of stimuli for different tasks

The CUSTOM algorithm is composed of three different packages: one for estimation, one for comparison and another one for the PANAmath algorithm (Halberda, Mazzocco & Feigenson, 2008). Each package includes the main function, a script that draws the stimuli, and some scripts that are meant to provide an example of how the main function can be used iteratively for creating full sets of stimuli with specific criteria. For instance, one of those scripts can be used to generate a set of stimuli following the same criteria adopted by the influential study of Piazza et al. (2004). We also included other scripts that can be used to generate a novel set of stimuli based on precise rules: for instance, one script has been used to generate two sets of stimuli for a hypothetical estimation task (described in the Testing the Algorithm paragraph). Note that these scripts are intended as mere examples: indeed, the algorithm can be efficiently used to generate sets of stimuli for estimation, habituation, comparison and match-to-sample tasks with novel criteria. For the estimation task, no other parameters are required to be set besides those already described in the previous paragraphs. Similarly, the algorithm can generate stimuli for habituation task with no additional specifications. In this case, the user has to pay attention to the numerosity of the habituation stimuli in relation to that of the deviant ones. Apart from that, no further parameters need to be specified.

The comparison task is more complex because the stimuli are composed by two arrays of elements. Thus, generating stimuli for the comparison task requires additional parameters related to the second array of elements: the numerosity, the desired control for the sizing aspects and the desired control for the placing aspects. Notably, it is possible to fully dissociate the control criteria applied to the two arrays composing the stimulus. However, when creating an entire set of stimuli for the comparison task, it is highly recommended to keep track of the ratio of numerosity and the ratio of visual features, which are thought to be crucial when designing the stimuli for a comparison task paradigm. Indeed, an imbalance between the ratio of numerosity and the ratio of visual features could cause a bias in favor of the most salient aspect of the stimulus, that is the one with a smaller ratio (DeWind & Brannon, 2016). The congruency between numerosity and visual features is another parameter that needs to be controlled. As a default setting, for each pair of numerosities, the algorithm creates a congruent and an incongruent trial. This function can be observed in the illustrative script included in the comparison package. For what concerns the match-to-sample task, two main aspects need to be manipulated: the dimension that connects sample and match stimuli (e.g., numerosity and/or one or more visual features, depending on the design) and the change ratio along this dimension across the comparison stimuli. Finally, it is worth mentioning that the PANAmath package introduces improved controls of convex hull that are not included in the original version of the method: it is possible to apply the control to the whole stimulus (i.e., both colors), but it is also possible to control separately the convex hulls of the two arrays of different color, even if the two arrays are fully overlapped. Obviously, it is not possible to control at the same time the overall convex hull and the convex hulls of the two array of different color.

Additional functionalities

The algorithm is enriched with two other functionalities that can be very useful, albeit not being mandatory for the generation of stimuli. One concerns density, which cannot be directly manipulated, because it is the result of total surface divided by convex hull. In our algorithm, density can be (albeit indirectly) manipulated with high precision (up to the fourth decimal), by simultaneously controlling the values of both these parameters. Furthermore, as an alternative to the classical formula to calculate density, we defined a new measure that might be closer to the concept of “interitem spacing,” which is often referred to when describing density (e.g., Gebuis & Reynvoet, 2011; Piazza et al., 2004). This new measure, called average distance between dots (included in the info file of each stimulus generated by the algorithm), corresponds to the length of the shortest open path connecting all the dots of the stimulus, divided by the number of dots minus one.

The other functionality that is worth mentioning is aimed at providing a user-friendly experience. The algorithm is equipped with an error system capable of detecting input parameters that violate the geometrical constraints. Starting from the input parameters, the function attempts to generate a stimulus with the desired characteristics but, if the number of attempts is exceeded (default: 1,000 attempts), an error message will show up indicating which part of the generation process was impossible to accomplish and suggesting which parameters should be modified. For instance, when attempting to generate a stimulus with 50 large dots in a small convex hull, after 1,000 failed attempts, the function will return the message “Number of iterations exceeded trying to place too many or too big dots in a small area while generating numerosity 50.” Also in this case, the number of attempts can be selected by the user; if an extreme set of input parameters is inserted (e.g., a large number of large dots enclosed in the smallest convex hull possible), a high number of attempts (and consequently, a longer waiting time per stimulus) is needed in order to generate stimuli with such features. This error system might facilitate the use of the algorithm, providing a valuable feedback that helps the user to avoid configurations of visual features that are geometrically impossible.

Testing the algorithm

The performance of the CUSTOM algorithm was tested by generating two sets of stimuli for a hypothetical estimation task, including five numerosities: 18, 23, 30, 40, and 52. The Matlab function was run on a MacBook Pro from early 2015: 2.7-GHz CPU and 8 GB DDR3 RAM. The original dimensions of all the stimuli of both sets were 500×500 pixels; 100 were generated for each numerosity, for a total of 500 stimuli per set. The objective was to create stimuli with a constant convex hull of 90,000 pixels across numerosities and across sets, by using the same manipulation in the placing phase for each one. On the other hand, the sizing manipulations were radically different in the two sets: We aimed at creating stimuli with a constant total contour of 3,000 pixels across numerosities in the first set (SET 1), and stimuli with a constant total surface of 30,000 pixels across numerosities in the second set (SET 2). The choice of such values for total contour (SET 1) and total surface (SET 2) was guided by comparative purposes, since they allowed to obtain a comparable average size of the dots a across the two sets. Such similarity, together with the equivalent convex hull, allows both the difference in the manipulation of sizing and the consistency in the manipulation of placing to emerge more evidently in the comparison. Finally, we manipulated the tolerance parameter of the convex hull for testing purposes: The first set had a tolerance of .005, and the second had a tolerance of .001.

Generating full sets of stimuli required the use of a simple script that runs the function iteratively, progressively changing the parameters (including numerosity) that are manipulated across stimuli. The resulting stimuli, their visual features, and the time needed to generate them are shown in the next section.

Results

The two sets of stimuli, generated for comparative purposes (see the Method section), served as a framework, to show (1) how the meticulous control embodied in the algorithm could yield a remarkable level of precision in manipulating visual features (in our example convex hull, total contour and total surface), and (2) how these manipulations dramatically affect the internumerosity variation of the nonmanipulated features (i.e., average diameter, density and average distance between dots) while simultaneously preserving low intranumerosity variability.

Sizing phase: Dot size manipulation

The target values for total contour (3,000 pixels in the first set, SET 1) and total surface (30,000 pixels in the second set, SET 2) were achieved with a high level of precision: The standard deviation was 0 for each numerosity in both sets (note, indeed, that in Fig. 3, SET 1.B and SET 2.C have no error bars). Manipulating one of the two features induced only a negligible intranumerosity variability in the other one (e.g., for N = 30; SET 1: total surface M = 26,287 pixels, SD = 525 pixels; SET 2: total contour M = 3,266 pixels, SD = 16 pixels). It should be noted that the two manipulations produce opposite tendencies: When total contour is constant, total surface decreases as numerosity increases (Fig. 3, SET 1.B and SET 1.C); when total surface is constant, total contour increases as numerosity increases (Fig. 3, SET 2.B and SET 2.C). Instead, average diameter decreases in both sets as numerosity increases; this is an obvious geometrical consequence that always applies if either total contour or total surface is held constant across numerosities. As we stated in the Method section, the values for total contour (SET 1) and total surface (SET 2) were selected so as to have comparable average dot diameters across the two sets (SET 1 = 34 pixels; SET 2 = 35 pixels), although the two manipulations caused different trends in the change of average diameter across numerosities: SET 1 included a wider range of diameters and a more noticeable change of average diameter across numerosities than did SET 2 (Fig. 3D and Fig. 4 for visual examples). This difference emerged because the addition or subtraction of dots affects total contour (SET 1) way more than total surface (SET 2). The wider range of dot diameters in SET 1 in turn caused a larger variability of total surface in SET 1 with respect to total contour in SET 2.

Fig. 3
figure 3

Series of graphs showing the effects of changes in numerosity over specific visual features. The first column corresponds to SET 1, and the second column corresponds to SET 2. The letters correspond to the visual features: A = convex hull, B = total contour, C = total surface, D = average diameter, E = “classic” density, and F = average distance between dots

Full size image
Fig. 4
figure 4

Examples of one stimulus for each numerosity, extracted from both SET 1 (top row) and SET 2 (bottom row). The same numerosities from different sets can be compared across columns

Full size image

Placing phase: Convex hull manipulation

The target value for convex hull (90,000 pixels) was achieved in both sets (Fig. 3A). The only difference in the manipulations of convex hull between the two sets resided in the tolerance parameter applied to the two sets: SET 1 was generated with a tolerance parameter of .005, whereas SET 2 was generated with a tolerance parameter of .001. This difference affected the precision of the convex hull manipulation at the single-stimulus level, as well as the time needed for generating the stimuli. As is shown in Fig. 3A, the overall precision was unaffected by the different tolerance parameters (SET 1, M = 89,998 pixels; SET 2, M = 90,000 pixels); the precision at the single-stimulus level increased in SET 2, in which the tolerance parameter was more stringent (SET 1, SD = 129 pixels; SET 2, SD = 26 pixels), although this difference was too small to be shown graphically with error bars in the SET 1 graph (Fig. 3, SET 1.A).

The 500 stimuli of SET 1 were generated on a MacBook Pro from early 2015, 2.7-GHz CPU and 8 GB DDR3 RAM, in 22 min and 57 s (2.75 s per stimulus), and the 500 stimuli of SET 2 were generated on the same machine in 26 min 40 s (3.2 s per stimulus). It is worth mentioning that if the two sets had undergone the same sizing manipulation, the difference in the times needed would have been even more noticeable.

The issue of density

The results show that the CUSTOM algorithm can provide precise control over density (classically defined as total surface divided by convex hull); in SET 1, density decreased as numerosity increased, because total surface also decreased as numerosity increased (Fig. 3, SET 1.E), whereas in SET 2 (Fig. 3, SET 2.E), the mean density of the set was constant across numerosities (0.333, resulting from 30,000 pixels of total surface divided by 90,000 pixels of convex hull). Notably, the intranumerosity variability was once again close to nil (e.g., for N = 30: SET 1, convex hull SD = 0.0058; SET 2, convex hull SD = 0.0001).

We also implemented an alternative method, encompassing interitem spacing as a pivotal concept to be taken into account, that led to the calculation of the average distance between dots (see the Method section), a measure that can often diverge from the “classical” density, as is shown in the following examples. In SET 1, the classical measure of density is not constant across numerosities, but it does not show intranumerosity variability; conversely, average distance between dots reaches a plateau at N = 30, and shows a sizable intranumerosity variability, which decreases as numerosity increases (Fig. 3, SET 1.F). In SET 2, the different patterns between the two measures are even more noticeable: While the classical density is constant across numerosities (with no intranumerosity variability), the average distance between dots, aside from showing intranumerosity variability, decreases as numerosity increases. Intuitively, the increase in numerosity induces the dots to be closer to each other, thereby causing a more crowded stimulus (see Fig. 3, SET 2.F, and Fig. 4 for visual examples). A typical arrangement of the two sets for the different numerosities can be observed in Fig. 4.

Discussion

The purpose of the present work was to present an algorithm that can provide scientists in the field of nonsymbolic numerical cognition with a versatile instrument to generate visual stimuli in an unbiased theoretical framework. The core strengths of the algorithm (standardization, precision, universality, and customization) are explained and discussed below.

The currently available methods are supposed to provide a reasonable performance for what concerns the precision in controlling the visual features, but a straightforward comparative evaluation across methods is challenging because of the lack of a proper standardization. In previous methods, the visual features are often precisely  defined from a conceptual point of view, but their operational implementation does not always fully adhere to the corresponding theoretical framework (see Salti et al., 2017). Furthermore, studies using modified versions of a previous algorithm are not uncommon (e.g., Gebuis & Reynvoet, 2012a; Szűcs, Nobes, Devine, Gabriel, & Gebuis, 2013); unfortunately, if detailed information about the specific modifications is not provided, replicating the exact manipulations performed could be very difficult. This aspect is of crucial importance if we consider that performance in a dot comparison task can be noticeably influenced by the visual controls (Clayton, Gilmore, & Inglis, 2015). In this regard, our new algorithm offers a major advantage in terms of standardization. The Matlab function does not need to be modified in order to accomplish different types of manipulation; indeed, the script running iteratively the function is the only part that needs to be modified, according to the user’s need. Having a unique algorithm capable of replicating previous sets and implementing new ones could enhance the communication in the field, because researchers might benefit from a common ground of measurement units, customizable parameters and unavoidable geometrical constraints.

Beside the standardization potential, the CUSTOM algorithm offers a remarkable precision: The chosen sizing visual feature (diameter, total surface or total contour) can be controlled at the pixel level, as shown in the results: The algorithm successfully created a set of images with total surface or total contour tied to a specific number of pixels, with no variability across stimuli. The manipulation of convex hull implemented in our algorithm also represents a significant step forward in terms of precision. Most of the previous algorithms manipulated the area in which the elements could be placed, introducing the interchangeable concepts of “total occupied area” (Izard & Dehaene, 2008; Piazza et al., 2004), “stimulus area” (Gebuis & Reynvoet, 2011), and “field area” (DeWind et al., 2015). Unfortunately, this type of procedure can have two drawbacks: First, it might not provide a stringent control of the convex hull, and also, in order to break the correlation between convex hull and numerosity, it forces to rely on a broad intra- and internumerosity variability (e.g., Gebuis & Reynvoet, 2012b). Instead, our algorithm achieves an extremely high precision in controlling the value of the convex hull—while narrowing down its variability across stimuli to negligible values—by incorporating a conceptually opposite approach based on the iterative procedure described in the Method section. Note that input parameters and output values of each stimulus are stored in a .csv file: Including this file in the supplementary material would ensure a higher level of transparency and replicability in this research field.

Another core strength of the CUSTOM algorithm resides in its multipurpose nature. As far as we know, all the currently available algorithms have a very specific use: Most of them are built for comparison tasks (e.g., Gebuis & Reynvoet, 2012a; Halberda et al., 2008), few of them are built for estimation tasks (e.g., Gebuis & Reynvoet, 2012b), and some of them embody a theory-driven approach (e.g., DeWind et al., 2015; Piazza et al., 2004). Unlike those methods, our algorithm is virtually able to reproduce the characteristics of any set of stimuli described in any experiment on numerical cognition conducted so far: It can generate stimuli for estimation, comparison, habituation, and match-to-sample tasks, providing at the same time full freedom of choice to the user for what concerns the selection of the visual features. A wider customizability of the stimuli should be regarded as an essential aspect, because it might constitute a driving force to start addressing not only if, but also how a continuous magnitude contributes to numerical perception (see Salti et al., 2017).

Besides these main advantages, other topics need to be discussed because of their theoretical repercussions. A more subtle—albeit not less critical—point concerns the implicit connection between the algorithms and theories on numerical cognition: although in some instances this might represent an unavoidable consequence, it should be noted that some algorithms might potentially create a bias in favor of a specific theory. For instance, a quite popular approach in comparison tasks requires a classification of the trials on the basis of the congruency between numerosity and visual features, thereby guiding users toward a Stroop-like interpretation of the results (see Gebuis & Reynvoet, 2012a; Salti et al., 2017). Our algorithm minimizes this risk by having an “unbiased,” atheoretical nature, that does not force the user to adopt a specific theoretical framework. It is the job of the user to find the proper set of parameters needed to create stimuli suited for testing a specific hypothesis. For instance, we recently created a set of stimuli with constant convex hull, composed by three numerosities (25, 30, 36) and three levels of dot size (small, medium, large) manipulated through total contour. This set of stimuli was used in an estimation task that included a calibration phase based on the visual features of the calibration stimuli (Abalo-Rodriguez, De Marco & Cutini, under review). The algorithm was able to produce stimuli with no correlation between numerosity and average distance between dots within each dot size subset. Notably, this manipulation is sophisticated, but it does not embrace in aprioristic fashion any theory.

Even though we underlined the flexibility of the algorithm in generating stimuli for different tasks, we think it is necessary to strike a blow for the estimation task over the comparison task. Despite being the most used task in the field, comparison tasks are limited by the dichotomous nature of its response code (Leibovich, Khadim, & Ansari, 2017a), and they have been criticized because they call into play inhibitory resources to resolve the conflict induced by the incongruency between numerosity and the amount of visual features across the to-be-compared stimuli (Clayton & Gilmore, 2014; Szűcs et al., 2013). On the other hand, the estimation task could provide a measure of numerical perception uncontaminated by inhibitory resources, thanks to the analog response code required to perform the task and the presence of a single stimulus to be evaluated. Puzzlingly enough, estimation tasks have been underused in the recent years, even though they provided insightful results about specific (Gebuis & Reynvoet, 2012b) and/or contextual (Leibovich, Khadim, & Ansari, 2017a) effects of visual features on numerical perception. The CUSTOM algorithm might hopefully lead to an increasing interest toward the estimation task, since it can readily create sets of stimuli ideally suited for such paradigm.

Another important consideration concerns the control of density: since both total surface and convex hull can be simultaneously manipulated with high accuracy, the algorithm ensures a stringent control over the “classical” density parameter (i.e., total surface divided by convex hull). Moreover, we created another metric—called average distance between dots—which uses interitem spacing as a pivotal element for measuring density. The rationale stems from the limitations imposed by the classical measure of density, which does not take into account some aspects of the stimuli such as numerosity, dots’ arrangement and clustering. As is shown in the results, stimuli with equal total surface and convex hull but different numerosities share an identical “classical density,” while having a different average distance between dots. It is conceivable to argue that, at least in some circumstances, the classical density measure might not adequately capture all the physical aspects of the stimuli that might be potentially relevant. Besides total surface and convex hull, this perspective calls for a deeper investigation about the impact of other factors (such as numerosity), on the perception of density.

One last point concerns the use of “sizing” and “placing” as concepts that have been introduced in the method. Despite their similarity with the terms used by DeWind et al. (2015; i.e., sizing and spacing), there is a fundamental difference. According to DeWind and colleagues, the independence (or orthogonality) of sizing, spacing, and numerosity is preserved at any stage (from the creation of the stimuli to the interpretation of the results). Our method suggests that such independence is restricted to the manipulation phase: sizing and placing can be manipulated separately and independently, but manipulating one feature will unavoidably influence the other ones. According to our algorithm, even the smallest variation of the diameter of a single dot in a stimulus will slightly influence all the other visual features of the stimulus; if the modified dot is in external position, even convex hull will be affected.

In conclusion, we believe that the field of nonsymbolic numerical cognition is currently afflicted by issues in both replicability and comparability across studies. We suspect that this might be a direct consequence of the vast amount of different ideas, points of view and theories discussed in the field. For instance, a recent review suggesting a novel interpretation of the number sense theory (Leibovich, Katzin, et al., 2017b) triggered a large number of responses in the open peer commentary section. It is of paramount importance to note that all these different approaches are always being tested with different paradigms, different sets of stimuli, different manipulations and different measures of the visual features. A common methodological framework, based on shared standardized procedures, is currently lacking: in this regard, the CUSTOM algorithm could represent an asset in the field of numerical cognition, as a versatile instrument for effectively generating high precision visual stimuli within an unbiased theoretical framework.