Introduction

In item response theory (IRT,) a set of items, the instrument, measures a latent variable describing a person. The latent variable could be for instance math skills, the level of depression, or quality of life. In IRT models it is assumed that items are conditionally independent given the latent variable. This technical requirement that the items should only be correlated through the latent trait that the test is measuring is referred to as local independence and is well described in the literature (Lord & Novick, 1968; Lazarsfeld & Henry, 1968).

The assumption of local independence can be violated in different ways. Firstly, instruments are often composed of item bundles each measuring their own aspect of the latent variable and the higher-order latent variable alone might not account for correlations between items in the same bundle. This type of local dependence can be interpreted as a violation of unidimensionality. Secondly, the assumption of local independence can be violated if the response given to one item directly influences the response given to another item. This may happen due to similarities in item content or in response format or, in an educational test, if the correct answer on the first item contains a clue as to the correct answer for the second item.

Both of these situations yield inter-item correlations beyond what can be attributed to the latent variable, but for very different reasons. In order to distinguish between these two types of dependence, the first one is sometimes termed trait dependence and the second one response dependence. In general, trait and response dependence are not clearly distinguished in the literature. Nevertheless, using algebraic formulations of the two phenomena, Marais and Andrich (2008a, b) have demonstrated that the implications of the two types of dependence point in opposite directions. One of the important observations is that reliability indices (the person separation index and Cronbach’s coefficient alpha) decrease for data with trait dependence, but increase for data with response dependence. Thus, the reliability of an instrument should be interpreted with caution if the assumption of local independence has not been carefully checked.

Methods for detecting both types of local independence in Rasch models have been proposed by Kelderman (1984). He expressed the dichotomous Rasch model as a log-linear model and then showed that local dependence corresponds to interactions between items in the resulting log-linear Rasch model. Kelderman’s (1984) original model was for dichotomous item only, but log-linear Rasch models for polytomous item formats also exist (Kelderman, 1997).

Log-linear Rasch models have also been considered by Kreiner and Christensen (2004, 2007). Motivated by Tjur (1982), they evaluated partial correlations between item pairs conditionally on rest scores. This approach is similar to the Mantel–Haenszel analysis of differential item functioning (DIF) (Holland & Thayer, 1988; Holland & Wainer 1993) and is readily implemented in standard software. Kreiner & Christensen argue that models that incorporate local dependence still provide essentially valid and objective measurement and describe the measurement properties of such models.

Methods for detecting local dependence in IRT models that are more complicated than Rasch models include the use of conditional covariances (Douglas et al., 1998), Mantel–Haenzsel type tests (Ip, 2001), or specification of models that incorporate local dependence (Hoskens & De Boeck, 1997; Ip, 2002). Furthermore, papers have addressed consequences of local dependence (Scott & Ip, 2002) and ways of adjusting for it (Ip, 2000).

Jiao and colleagues proposed a three-level hierarchical generalized linear model (HGLM) to model clustered data like this and compared it to the Rasch-equivalent two-level HGLM that ignores the nested structure of items (Jiao et al. 2005). The result of fitting the too simple model was imprecise estimation of item difficulties and underestimation of the variance in the distribution of the latent variable. Modeling the structure estimated the variance in the distribution of the latent variable correctly, while the two-level HGLM increasingly underestimated the variance as the magnitude of dependence increased.

Another formalization of local dependence in IRT models is the notion of testlets, i.e., groups of items that are placed on a test as a unit, typically reading passages followed by a group of questions (Bradlow et al., 1999; Wang & Wilson, 2005). When evidence of local dependence turns up, constructing testlets post hoc can be a solution that permits the use of conventional unidimensional IRT models even in the presence of local dependence (Yen, 1993).

Confirmatory factor analysis (CFA) models are applied to describe correlation structures, and have been formulated for latent response variables measured using ordinal categorical observed variables (Muthén, 1979, 1984). Confirmatory factor analysis can be used to test local dependence across time points by considering models with an added covariance parameters.

Common to the HGLM, the testlet model and the CFA approach is that they all model dependence using random effects. This means that they are methods for modeling trait dependence. As for response dependence, a way of quantifying this has been proposed by Andrich and Kreiner (2010) for two dichotomous items. It is based on splitting one of the items into two new items according to the responses to the other item. The magnitude of dependence is then estimated as half the distance between the estimated item locations of the new items. A generalization of this approach to polytomous items was later proposed (Andrich et al., 2012).

Beyond local item dependence, local person dependence can also occur in case of cluster sampling (Jiao et al., 2012), however this is not discussed in this paper.

Longitudinal extensions of IRT models have been proposed (Andersen, 1985; Embretson, 1991; Liu & Hedeker, 2006; Bousseboua & Mesbah 2010). Many of these impose an additional requirement of local independence across time points. In these models, correlations between responses for the same person are modeled by including a latent correlation matrix. However, when the same measurement instrument is used at two time points, correlations between responses for the same person might be stronger than what the latent variable accounts for. If this is the case, the requirement of local independence across time points is violated by response dependence. Marais (2009) has shown that ignoring response dependence can either mask or exaggerate changes in both items and persons potentially leading to wrong conclusions. It is therefore important to be able to deal with this type of dependence.

Another key assumption when measuring trends over time is that the item parameters do not change over time (Wells et al., 2002; Miller and Fitzpatrick 2009). This can be considered differential item functioning with respect to time and is often referred to as item parameter drift. In many applications, persons are followed over time in order to measure change in some latent variable. For that purpose, the measurement instrument should be somewhat stable in the sense that there is no item drift. Tests of this assumption have been proposed and implemented in SAS by Olsbjerg and Christensen (2013a, b) for the special case of the Rasch (1PL) model. DIF across time, or item parameter drift, describes the situation where the parameters of an item changes for everybody in the population, while local dependence across time, as operationalized here, describes the situation where the parameters of an item at the second time point depends on the response given to the item at the first time point. Thus, these are different phenomena, but it should be noted that in the case of local dependence across time points, spurious evidence of item parameter drift can turn up: Consider for example a situation where a test item becomes much easier for the 80 % of subjects who answer correctly at time point 1, but retains its difficulty for the remaining 20 % of the population. In this situation, the item will appear to have item parameter drift.

In this paper we propose a method for modeling response dependence in a longitudinal version of the 2PL model. This way, unbiased estimation of change in the latent variable becomes feasible. It is based on the idea by of splitting dependent items in unidimensional Rasch models of Andrich and Kreiner (2010), see also Andrich et al. (2012). Henceforth, we use the term local dependence when referring to response dependence.

The 2PL model

The dichotomous Rasch (or 1PL) model (Rasch, 1960; Fischer and Molenaar, 1995) and the Birnbaum (or 2PL) model (Birnbaum, 1968) are the simplest IRT models. They describe the responses to manifest dichotomous items X 1,…,X I measuring a latent variable \(\theta \in \mathbb {R}\). The response probability for item i for a given value of 𝜃 is modeled as

$$\begin{array}{@{}rcl@{}} P(X_{i}=x_{i}|\theta)&=&\frac{\exp[x_{i}\alpha_{i}(\theta-\beta_{i})]}{1+\exp[\alpha_{i}(\theta-\beta_{i})]}(i=1,\ldots,I) \end{array} $$
(1)

where the discrimination α i and the threshold β i are parameters describing the items and 𝜃 a parameter describing the person responding. The special case of Rasch models appears when the discrimination parameter is constant across items α 1=...=α I . Usually the α’s are fixed at 1 and the variance in the distribution of the latent variable is estimated, but alternatively the variance can be fixed and the common value of the discrimination can be estimated. A technical assumption in both of these models is that items are locally independent

$$\begin{array}{@{}rcl@{}} &&{}P(X_{1}=x_{1},...,X_{I}=x_{I}|\,\theta) \\ &&=\prod\limits_{i=1}^{I}P(X_{i}=x_{i}|\theta)\textrm{ for all }\theta\in\mathbb{R}. \end{array} $$
(2)

and furthermore that persons respond independently of each other. For persons v=1,...,N with response vectors \(\overline {X}_{1},...,\overline {X}_{N}\), these two independence assumptions yields the joint likelihood

$$\begin{array}{@{}rcl@{}} &&{}L(\overline\beta,\theta_{1},\ldots,\theta_{N}\,|\,\overline{x}_{1},...,\overline{x}_{n}) =\prod\limits_{v=1}^{N}Pr(\overline X_{v}=\overline x_{v}|\theta_{v})\\ &=&\frac{\exp[{\sum}_{v}\theta_{v}{\sum}_{i=1}^{I}\alpha_{i} x_{vi}-{\sum}_{i}\alpha_{i}\beta_{i}x_{.i}]}{{\prod}_{v=1}^{N}{\prod}_{i=1}^{I}[1+\exp(\alpha_{i}(\theta_{v}-\beta_{i}))]}. \end{array} $$
(3)

The model is only identified if restrictions are placed on either the item parameters or the latent variable. One option is to assume that either \({\sum }_{i=1}^{I}\beta _{i}=0\) or \({\sum }_{v=1}^{N}\theta _{v}=0\) and \({\prod }_{i=1}^{I}\alpha _{i}=1\) or \({\prod }_{v=1}^{N}\theta _{v}=1\). Estimation based on the likelihood (3) leads to inconsistent estimates (Neyman & Scott, 1948). For this reason, either marginal maximum likelihood (MML) estimation (Bock & Aitkin, 1981; Thissen, 1982; Zwinderman & van den Wollenberg, 1990), or in the special case of Rasch models conditional maximum likelihood (CML) estimation (Andersen, 1973) can be used.

The longitudinal 2PL model

For time points t=1,...,T let X 1t ,…,X I t be a set of dichotomous items measuring a value \(\theta _{t}\in \mathbb {R}\) of the latent variable, where measurements for the same person at two time points t 1 and t 2 are correlated, \(\text {Corr}(\theta _{t_{1}},\theta _{t_{2}})>0\). Assume that at all time point t all items i fit the 2PL-model

$$\begin{array}{@{}rcl@{}} P(X_{it}=x_{it}|\theta_{t})&=&\frac{\exp(x_{it}\alpha_{it}(\theta_{t}-\beta_{it}))}{1+\exp(\alpha_{i}(\theta_{t}-\beta_{it}))} \end{array} $$
(4)

and that the assumption of local independence (2) holds within time point. It is tempting to further assume that responses to any two items i and j at any two time points t 1 and t 2 are locally independent

$$\begin{array}{@{}rcl@{}} P(X_{it_{1}} &=&x_{it_{1}},X_{jt_{2}}=x_{jt_{2}}|\,\theta_{t_{1}},\theta_{t_{2}})=P(X_{it_{1}}=x_{it_{1}}|\,\theta_{t_{1}})\\ && \times P(X_{jt_{2}}=x_{jt_{2}}|\,\theta_{t_{2}}) \end{array} $$
(5)

Doing so would lead to the generalization of Eq. 2

$$\begin{array}{@{}rcl@{}} P(\overline{\overline{X}}=\overline{\overline{x}}|\overline{\theta})&=&\prod\limits_{t=1}^{T}\prod\limits_{i=1}^{I}P(X_{it}=x_{it}|\theta_{t}) \end{array} $$
(6)

where \(\overline {\overline {X}}=(X_{it})_{i\in \{1,...,I\},t\in \{1,...,T\}}\) and \(\overline {\theta }=(\theta _{t})_{t=1}^{T}\). When (6) in fact holds, then estimation can be done using simple multivariate extensions of the 2PL model. Such extensions have been considered for Rasch models (Andersen, 1985; Embretson, 1991; Adams et al., 1997).

Unfortunately, the assumption (6) might not be justified. It seems plausible that responses to the same item at two different time points are dependent beyond what is explained by the underlying latent variable. Ignoring violations of Eq. 6 can lead to biased estimates of the latent variable (Marais & Andrich, 2008a; Marais, 2009), hence the assumption should be checked.

Formalization of local dependence across time

Henceforth, we consider the situation where responses to item i at different time points t 1<t 2 lead to a violation of Eq. 5. In this case, all we know is that

$$\begin{array}{@{}rcl@{}} P(X_{i1} &=& x_{i1},X_{i2}=x_{i2}|\,\theta_{1},\theta_{2})= P(X_{i1}=x_{i1}|\,\theta_{1}) \\ && \times P(X_{i2}=x_{i2}|\,X_{i1}=x_{i1};\,\theta_{2}) \end{array} $$
(7)

where indices 1 and 2 are short for t 1 and t 2, respectively. Hence, taking account of the local dependence means finding a way of modeling the conditional probabilities in Eq. 7. One option is to again turn to the 2PL model and assume that

$$\begin{array}{@{}rcl@{}} P(X_{i2} &=& x_{i2}|X_{i1} =x_{i1};\theta_{2}) \\ &&=\frac{\exp[x_{i2}\alpha^{*}_{i2}(x_{i1})(\theta_{2}-\beta^{*}_{i2}(x_{i1}))]}{1+\exp[\alpha^{*}_{i2}(x_{i1})(\theta_{2}-\beta^{*}_{i2}(x_{i1}))]} \end{array} $$
(8)

where \(\alpha ^{*}_{i2}(x_{i1})\) and \(\beta ^{*}_{i2}(x_{i1})\) are new item parameters depending on the response given to the item at time t 1. If no local dependence across time points is present the parameters will coincide \(\alpha ^{*}_{i2}(0)=\alpha ^{*}_{i2}(1)\) and \(\beta ^{*}_{i2}(0)=\beta ^{*}_{i2}(1)\).

Detection of local dependence across time

Methods for detecting local dependence across time points in longitudinal IRT models have not received much attention in the literature. One exception is a paper by Olsbjerg and Christensen (2013a) where two tests in Rasch models are suggested. One of the tests discussed is to consider more general models that include interaction terms to account for local dependence between items at different time points. The longitudinal Rasch model can then be tested against these using likelihood ratio tests. This test can easily be extended to the 2PL model. The second test exploits sufficiency of the sum score and use Mantel–Haenszel tests for association between items conditioning on this. This works only for Rasch models.

Modeling local dependence

The formalization (8) results in joint probabilities that are products of 2PL model probabilities

$$\begin{array}{@{}rcl@{}} &&{} P(X_{i1}=x_{i1},X_{i2}=x_{i2}|\,\theta_{1},\theta_{2}) \\ &&=P(X_{i1}=x_{i1}|\theta_{1})P(X_{i2}=x_{i2}|X_{i1}=x_{i1};\theta_{2}) \\ &&=\frac{\exp[x_{i1}\alpha_{i1}(\theta_{1}-\beta_{i1})]}{1+\exp[\alpha_{i1}(\theta_{1}-\beta_{i1})]} \frac{\exp[x_{i2}\alpha^{*}_{i2}(x_{i1})(\theta_{2}-\beta_{i2}^{*}(x_{i1}))]}{1+\exp[\alpha^{*}_{i2}(x_{i1})(\theta_{2}-\beta_{i2}^{*}(x_{i1}))]}\\ \end{array} $$
(9)

In the special case of Rasch, Eq. 9 looks very similar to the longitudinal Rasch models of Andersen (1985) and Embretson (1991) where items are locally independent across time points. Except that in Eq. 9 the item parameter at time t 2 depends on the observed response at time t 1. Fitting this model is a matter of including the response at time point t 1 as a covariate that requires a modification of existing IRT software. An alternative way to go about it, well known in the framework of IRT models, is to recode (split) the items as illustrated in section “Item splitting”.

Item splitting

Item splitting is a standard method for handling differential item functioning (DIF), where the response probabilities of an item differ across subpopulations such as males and females. The idea of splitting items was proposed for Rasch models by Andrich and Kreiner (2010) in the context of quantifying the magnitude of local dependence.

Item splitting, used as a tool for modeling local dependence, can be adapted to longitudinal IRT models as follows. A dependent time t 2 item X i2 is split into two new items \(X_{i2}^{*}(0)\) and \(X_{i2}^{*}(1)\) representing the group of persons with a response at time t 1 of 0 and 1, respectively. Each person only contributes with an observed value to one of the new items, cf. Fig. 1.

Fig. 1
figure 1

Illustration of item splitting. To the left is a response matrix before the item splitting. To the right is the response matrix after splitting the dependent item X i2 into \(X_{i2}^{*}(0)\) and \(X_{i2}^{*}(1)\)

Full size image

Estimation of item parameters

Estimation of item parameters can be done using marginal maximum likelihood (MML) estimation assuming that \(\overline {\theta }=(\theta _{1},\theta _{2})^{T}\) follows a two-dimensional normal distribution

$$ \left[\begin{array}{c} \theta_{1}\\ \theta_{2} \end{array}\right]\thicksim \mathcal{N}_{2}\bigg(\left[ \begin{array}{c} \mu_{1}\\ \mu_{2} \end{array} \right], \left[ \begin{array}{cc} {\sigma_{1}^{2}}&\sigma_{1}\sigma_{2}\rho\\ \sigma_{1}\sigma_{2}\rho&{\sigma_{2}^{2}} \end{array} \right]\bigg) $$
(10)

where ρ = Corr(𝜃 1,𝜃 2) represents the latent correlation. Often the main interest is to estimate changes in the mean and variance leading to the reparameterization

$$\left[\begin{array}{c} \theta_{1}\\ \theta_{2} \end{array}\right]\thicksim \mathcal{N}_{2}\bigg(\left[ \begin{array}{c} 0\\ \mu_{2} \end{array} \right], \left[ \begin{array}{cc} 1&\sigma_{2}\rho\\ \sigma_{2}\rho&{\sigma_{2}^{2}} \end{array} \right]\bigg). $$

Let \(\varphi _{\overline {\mu },{\Sigma }}\) denote the density of Eq. 10. Then, for persons v = 1,...,N with response vectors \(\overline {X}_{v}=(X_{v11},...,X_{vI1},X_{v12},...,X_{vI2})\), the marginal likelihood has the form

$$\begin{array}{@{}rcl@{}} && L_{M}(\overline\alpha,\overline{\beta},\overline{\mu},{\Sigma}\,|\,\overline{x}_{1},...,\overline{x}_{N})\\ &&=\prod\limits_{v=1}^{N}{\int}_{\mathbb{R}^{2}}P(\overline{X}_{v}=\overline{x}_{v}|\overline{\theta})\varphi_{\overline{\mu},{\Sigma}}(\overline{\theta})d\overline{\theta} \end{array} $$
(11)

where \(\overline {\alpha }\) and \(\overline {\beta }\) denote the vectors of item discriminations and thresholds respectively, for both split and unsplit items. The probabilities in Eq. 11 are given by

$$\begin{array}{@{}rcl@{}} &&{}P(\overline{X}_{v}=\overline{x}_{v}|\overline{\theta}) = \prod\limits_{i=1}^{I}P(X_{vi1}=x_{vi1}|\theta_{1})P(X_{vi2} \\ &&= x_{vi2}|X_{vi1}=x_{vi1};\theta_{2}) \prod\limits_{i=1}^{I}\bigg(\frac{\exp[x_{vi1}\alpha_{i1}(\theta_{1}-\beta_{i1})]}{1+\exp[\alpha_{i1}(\theta_{1}-\beta_{i1})]}\bigg) \\ && \bigg(\frac{\exp[x_{vi2}\alpha^{*}_{i2}(x_{vi1})(\theta_{2}-\beta_{i2}^{*}(x_{vi1}))]}{1+\exp[\alpha_{i2}^{*}(x_{vi1})(\theta_{2}-\beta_{i2}^{*}(x_{vi1}))]}\bigg). \\ \end{array} $$
(12)

We can not measure change in the latent variable with a measurement instrument that changes completely. For that reason, it is important that some of the items remains the same, across time points, in the sense that

$$\alpha_{i1}=\alpha^{*}_{i2}(0)=\alpha^{*}_{i2}(1)\qquad\text{and} \quad\beta_{i1}=\beta^{*}_{i2}(0)=\beta^{*}_{i2}(1) $$

for i in some (reasonably sized) subset \(\mathcal {I}_{0}\subseteq \{1,...,I\}\). Again, restrictions on the parameters are needed in order for the model (11) to be identified. At each time point we have to put restrictions on either the item or population parameters. One option is to require that either \({\sum }_{i=1}^{I}\beta _{i1}=0\) and \({\prod }_{i=1}^{I}\alpha _{i1}=1\), or that μ 1 = 0 and \({\sigma _{1}^{2}}=1\), and similarly at time t 2.

The model (11) can be estimated in SAS using the NLMIXED procedure for fitting nonlinear mixed models. MML estimation is carried out by maximizing an approximation to the likelihood (11) integrating out the random effects. The SAS macro %LRASCH_MML (Olsbjerg & Christensen, 2013b) is an implementation of the special case of Rasch models. In this implementation, adaptive Gaussian quadrature is used for integral approximation and the Newton-Raphson algorithm for optimization. The SAS macro %LRASCH_MML (Olsbjerg & Christensen, 2013b) works for incomplete data, and for this reason, local dependence across time points can be modeled according to Eq. 8. Whether the effect of local dependence is significant can be evaluated by comparing the likelihood in Eq. 11 to the likelihood of the simple model based on the assumption of local independence (6) in a likelihood ratio test.

Estimation of person location parameters

Usually, it is of interest to estimate change at the individual level. In the previous section, we described how the item parameters can be estimated by assuming a certain distribution for the latent vector and then maximizing an approximation to the marginal likelihood. Estimation of the person parameters can be carried out in a similar manner by substituting the item parameters in Eq. 12 by their MML estimates \(\widehat {\overline {\alpha }}\) and \(\widehat {\overline {\beta }}\) resulting in the likelihood function

$$\begin{array}{@{}rcl@{}} L_{M}(\overline{\theta}\,|\,\overline{x}_{1},...,\overline{x}_{N})&=&L(\widehat{\overline{\alpha}},\widehat{\overline{\beta}},\overline{\theta}\,|\,\overline{x}_{1},...,\overline{x}_{N}) \end{array} $$
(13)

where

$$\begin{array}{@{}rcl@{}} L(\widehat{\overline{\alpha}},\widehat{\overline{\beta}},\overline{\theta}\,|\,\overline{x}_{1},...,\overline{x}_{N})&=&\prod\limits_{v=1}^{N}P(\overline{X}_{v}=\overline{x}_{v}|\overline{\theta}_{v}) \end{array} $$

is the joint likelihood with the estimated item parameters inserted. This corresponds to assuming a distribution of the item parameters which is degenerate in their estimated values. Estimates of \(\overline \theta _{v}\) can be derived from Eq. 13 by numerical optimization such as Newton–Raphson.

Thus, we can compute estimates \(\hat {\overline \theta }=(\hat \theta _{1},\hat \theta _{2})\) and change scores \(\hat {\theta }_{2}-\hat {\theta }_{1}\) for each person. This can be done in the model assuming local independence across time points and in a model that takes local dependence across time points into account. It is then possible to evaluate whether local dependence across time points affects the conclusions about individuals.

Simulation study

A simulation study was conducted to illustrate the implications of local dependence across time points and to illustrate the advantage of splitting items. Responses were simulated by (i) simulating person parameters from a two-dimensional normal distribution

$$\left[\begin{array}{c} \theta_{1}\\ \theta_{2} \end{array}\right] \thicksim\mathcal{N}_{2}\bigg(\left[ \begin{array}{c} 0\\ \mu \end{array} \right], \left[ \begin{array}{cc} 1&0.5\\ 0.5&1 \end{array} \right]\bigg) $$

(ii) simulating responses at time 1 from a 2PL model given the person and item parameters, and (iii) simulating responses at time 2 from the same dichotomous Rasch model with the exception that item thresholds for the locally dependent items were shifted by 1. More specifically, item thresholds for these items were given as

$$\beta_{i2}^{*}(0)=\beta_{i1}+1\qquad\text{and}\qquad\beta_{i2}^{*}(1)=\beta_{i1}-1. $$

This means that at time 2 the item becomes more difficult for those with a wrong response at time 1 and easier for those with a correct response at time 1 in the case where 0 and 1 represent an incorrect and correct response, respectively. In each case we simulated data sets with no change in the population mean across time points (μ = 0) and data sets where a change in the population mean (μ = 0.5) was present. We simulated 100 data sets with responses from N = 500 persons at two time points, to 24 dichotomous items with equidistant thresholds ranging from −2 to 2. We simulated data sets where the assumption of local independence across time points was violated for two, four, six, eight, and ten items, respectively. Furthermore, we simulated data sets with dependence for difficult items and dependence for easy items, respectively. An overview of the simulation setups is provided in Table 1.

Table 1 Overview of the simulation study
Full size table

For each simulated data set, we considered two ways of splitting items, no splitting and splitting of the item(s) with dependence. The effects of splitting an item without local dependence across time points were studied in some but not all simulations. Overview of the simulation study: setups 1 through 5 illustrate that the effect of local dependence across time increases with the number of affected items. Simulation setups 6 and 7 and simulation setups 6 and 7 illustrate the impact when the local dependence is for easy and difficult items, respectively. Each simulated data set was, after recoding locally dependent items (cf. Fig. 1), analyzed in SAS using PROC NLMIXED. The results are shown in Table 2.

Table 2 Simulation study results, 100 simulated data sets, N = 500 persons, 24 items (equidistant β 1 = −2,…,β 24 = 2)
Full size table

The results clearly show that the latent correlation ρ was only recovered in the rows labeled (ii), where the dependent item(s) were split. In rows labeled (i), where the dependent items were not split, ρ was consistently overestimated. When the number of dependent items increases the extent to which the latent correlation ρ is overestimated increases. In the part of Table 2 where the population mean changes over time (μ = 0.5) the change in mean was only recovered in where dependent item(s) were split. In setup (i), where no items were split, the mean change was underestimated. The extent to which the mean change was underestimated increased with the number of dependent items. There appeared to be little impact on the item parameter estimates (results not shown). The results of this simulation study indicate that local dependence across time points has an impact on estimates of the mean change in the latent variable, and on estimates of the latent correlation. The simulation study did not provide evidence of different impact of local dependence for difficult and easy items, respectively.

Example

The methods proposed in this paper will be illustrated using data collected in the Bradford Metropolitan Health District. A total of 113 persons with episodes of low back pain responded to the Roland and Morris (1983) disability questionnaire, consisting of 24 dichotomous items, at two time points. Further details about the data collection can be found elsewhere (Waxman et al., 1998).

We first analyzed the responses by fitting the unidimensional 1PL and 2PL models at each time point separately. Likelihood ratio tests were used to compare the two models. The results, summarized in Table 3, provide no justification for fitting the simpler 1PL model at any of the two time points.

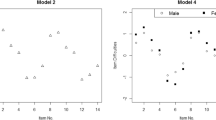
Table 3 Likelihood ratio tests of the 1PL model against the 2PL model, separately at each time point
Full size table

To take into account the longitudinal nature of the data, we fitted the generalized longitudinal 2PL model (9), which handles both items with time-varying parameters and local dependence across time points. In order to identify items with such characteristics likelihood ratio tests were conducted. These tests are described for the 1PL model (Olsbjerg & Christensen, 2013a), but are easily implemented in SAS for both the 1PL and the 2PL model. The assumption of time-invariant item parameters was first investigated graphically using the estimates derived from the two unidimensional models. Centralized item thresholds at the two time points are plotted against each other in Fig. 2 and standardized item discriminations in Fig. 3.

Fig. 2
figure 2

Item thresholds at time 1 and time 2

Full size image
Fig. 3
figure 3

Item discriminations at time 1 and time 2

Full size image

Further investigation of the assumption of time-invariant item parameters was done using a likelihood ratio test proposed by Olsbjerg and Christensen (2013a). This test is for DIF with respect to time based on MML estimation where, for each person, only responses at a single (randomly chosen) time point are used in order to get rid of possible local dependence. These tests suggested that item parameters for three items (items 2, 15, and 21) change over time. However, in light of the large number of statistical tests and the inherent risk of type I, we disregarded this evidence and we continued the analyses assuming that all item parameters were the same at both time points. This corresponds well with what was observed in the plots in Figs. 2 and 3, where the estimates were relatively evenly scattered around the diagonal. As expected, the variation in the estimated item discriminations across time points is noticeably larger than for the thresholds.

In order to identify items with local dependence across time points, likelihood ratio tests were conducted. These tests were proposed by (Olsbjerg and Christensen 2013a) for Rasch models but can easily be extended to the 2PL model. A total of eight out of the 24 items showed significant evidence of local dependence across time points. The results are summarized in Table 4.

Table 4 Item wording, estimated item parameters, and likelihood ratio tests for local independence across time points
Full size table

We chose as our final model the 2PL model that incorporates local dependence for the eight items with p-values below 5 %. Estimates from this model can then be compared to the estimates from the simpler 2PL model that ignores the dependence and where all items have equal parameters at the two time points. In Table 5, estimates of the population mean change and the latent correlation derived from the two models are displayed. The estimated population mean change differs only slightly between the two models. The estimated latent correlation decreases when items are split for dependence and this corresponds well with what was observed in the simulation study.

Table 5 Population parameter estimates for Model 1, the simple model where no items are split for dependence and Model 2, the final model where eight items are split for dependence
Full size table

To get a sense of how it might affect the individual respondents to ignore local dependence as compared to modeling it, we investigate the estimated person locations in the simple model and in the model taking local dependence across time into account. Keeping the item parameters fixed at their estimated values, we consider person location estimates and estimates of the change

$${\Delta}=\theta_{2}-\theta_{1} $$

in the latent variable for Model 1 and Model 2. The results, presented in Table 6, reveal that generally the difference between the two models is not that big.

Table 6 Summary of the estimated person locations (𝜃 1 and 𝜃 2) and of the individual change scores Δ=𝜃 2−𝜃 1 for the 113 persons in the data example. Model 1 is the simple model where no items are split for dependence and Model 2 the true model where the eight items showing signs of local dependence are split
Full size table

The two models do not differ with respect to the estimated time 1 person locations, but there appears to be more variability in the incorrect Model 1. Regarding the person locations at the second time point, there is a difference in that Model 1 appears to underestimate the values. Again, there is more variability in the incorrect model. The difference between the person time 2 person location estimates from Model 1 and Model 2 were larger than the differences between time 1 person location estimates.

Regarding change scores there was more variability when using the more correct model. A substantial variation in the difference between Δ values assigned to individuals was observed. A consequence of this variation is that the two models did not agree about who had a significant change score. This occurred for five out of the 113 people responding: 3 (2.7 %) who were considered to have a significant Δ value by Model 2, but not by Model 1 and 2 (1.8 %) who were considered to have a significant Δ value by Model 1 only.

Discussion

The assumption of local independence in unidimensional IRT models has been the focus of much research (Hoskens & De Boeck, 1997; Douglas et al., 1998; Ip, 2000, 2001, 2002; Scott & Ip 2002). In unidimensional IRT models, violations of this assumption can be resolved by changing the wording or the response categories of the items. Another solution is to use the sum of the dependent items as a so-called ’subtest’ (Andrich, 1985). Alternatively, a testlet model (Bradlow et al., 1999; Wang & Wilson, 2005) or other models taking account of local dependence (Hoskens & De Boeck, 1997; Ip, 2002) can be applied. In Rasch models, a simple way of quantifying local dependence has been proposed (Andrich and Kreiner, 2010).

In longitudinal studies where the same instrument is used at several occasions to measure change in a latent variable, the assumption of local independence across time points may well be violated. In that case, there is usually no desire to change the item content, and collapsing items across time points does not make sense in the context of measuring change.

This paper described how local dependence across time points can be modeled in longitudinal IRT models. Based on the method of item splitting by Andrich and Kreiner (Andrich and Kreiner (2010)), which has so far only been used for quantification of local dependence in unidimensional models, we proposed a general method that can be used to test for and model local dependence across time points. It should be noted that in the Andrich and Kreiner approach, the first item is discarded after recoding the second item, but that in the method proposed here we keep the time 1 item along both versions of the time 2 item. Because the method is based on item splitting, a concept well known for resolving differential item functioning (DIF), it can be used in existing software such as RUMM (Andrich et al., 2010)

The simulations incorporated local dependence in a way that made it more likely for a person to give the same response to an item at the two time points, than it would have been in the case of local independence. By fitting the simple model assuming local independence across time points for all items, we demonstrated some of the effects of ignoring local dependence, one of them being that the dependence was mistakenly accounted for by the latent correlation ρ, which as a result was overestimated. These patterns were visible in simulations with only a single dependent item and became even more pronounced when more items were dependent. Estimation of the change in the mean of the latent variable was also affected by local dependence across time points. Results suggest that when local dependence occurs for items located in the middle of the latent continuum (as was the case in the simulation study) the change in the mean of the latent variable is underestimated, whereas dependence for items located in one end of the continuum (as in the simulation study) lead to overestimation of the change in the mean of the latent variable. This finding corresponds well with Marais (2009) who found that in certain circumstances local dependence will exaggerate changes and in other circumstances it will mask them.

In the data example, an effect on the latent correlation, similar to those of the simulations, was found when dependence was ignored, but regarding the estimated mean change of the latent variable, no difference was found when splitting the items with signs of local dependence.

In the data examples and in the simulation study, estimation was done PROC NLMIXED estimating item parameters and the two-dimensional latent distribution by MML estimation. For the special case of the Rasch (1PL) model, estimation can also be carried out in RUMM (Andrich et al., 2010) by splitting dependent items, fitting the model at each time point and then comparing person estimates. We considered dichotomous items administered at two time points. The proposed method is easily generalized to polytomous items because it is based on the simple concept of item splitting. For that reason, it can also be adapted to other IRT models. In principle, it is also straightforward to make extensions to accommodate more than two time points. However, estimating the latent correlation matrix can become computationally challenging. Moreover, the splitting procedure can potentially become quite complex and lead to situations with sparse data if we allow for dependence structures that go beyond items at two consecutive time points.

Differential item functioning identified in relation to time is another phenomenon that occurs in longitudinal studies (Specht et al., 2011). This is often called item parameter drift (Wells et al., 2002; Miller & Fitzpatrick, 2009) and the assumption that item parameters are stable over time should also be tested. Different methods for detection of item parameter drift exist (Donoghue & Isham, 1998; DeMars, 2004; Galdin & Laurencelle, 2010). In the data example and in the simulation study, we assumed that item parameters were stable over time, but for the special case of Rasch models, the SAS macro lrasch_mml (Olsbjerg & Christensen, 2013b) can be used to test this assumption using likelihood ratio tests. Since local response dependence formulated using item splitting is also implemented, this yields a modeling framework where items that change over time and items with local dependence across time points can be included. This model can be fitted using two-dimensional MML including three types of items: items with local dependence across time points, items with DIF across time points, and items with neither. Items with local dependence across time points are included by splitting the time 2 item and estimating \((\alpha ^{*}_{i2}(0),\beta ^{*}_{i2}(0))\) and \((\alpha ^{*}_{i2}(1),\beta ^{*}_{i2}(1))\), items with DIF across time points are included by the restriction \(\alpha ^{*}_{i2}(0)=\alpha ^{*}_{i2}(1)\) and \(\beta ^{*}_{i2}(0))=\beta ^{*}_{i2}(1))\), and items with neither can be included by the further restriction \(\alpha ^{*}_{i2}(0)=\alpha ^{*}_{i2}(1)=\alpha _{i1}\) and \( \beta^*_{i2}(0)=\beta^*_{i2}(1)=\beta_{i1}\).

For investigating local dependence across time points for a single item, the proposed methodology yields a likelihood ratio test. In a realistic situation with many items in a test, care must be taken to control the type I error rate by adjusting for multiple testing using e.g., the Benjamini–Hochberg (1995) procedure.

The methodology outlined in this paper is a simple way of accounting for local item dependence, while local person dependence was not discussed. However, this can also occur, and quite general methods for handling this using a four-level IRT model to simultaneously account for dual local dependence due to item clustering and person clustering have been proposed by (Jiao et al. 2012). The simple approach of taking dependence into account using item splitting proposed in this enables researchers to include local dependence in simpler multilevel models (Kamata, 2001). However, when an item X i2 is split for local dependence, fewer persons will contribute to the estimation the new item parameters \(\beta _{i2}^{*}(0)\) and \(\beta _{i2}^{*}(1)\) than to the original parameter β 2i . Hence, splitting items is at the cost of precision of the item parameter estimates and should only be done when there is evidence of local dependence. In the data analysis, the sample size was 113 and the 2PL model was fitted to the data, but the proposed methods were able to disclose evidence of local dependence across time points, and to model these. However, the proposed methodology should not uncritically be used in applications with small sample sizes.