BootES: An R package for bootstrap confidence intervals on effect sizes

Abstract

Bootstrap Effect Sizes (bootES; Gerlanc & Kirby, 2012) is a free, open-source software package for R (R Development Core Team, 2012), which is a language and environment for statistical computing. BootES computes both unstandardized and standardized effect sizes (such as Cohen’s d, Hedges’s g, and Pearson’s r) and makes easily available for the first time the computation of their bootstrap confidence intervals (CIs). In this article, we illustrate how to use bootES to find effect sizes for contrasts in between-subjects, within-subjects, and mixed factorial designs and to find bootstrap CIs for correlations and differences between correlations. An appendix gives a brief introduction to R that will allow readers to use bootES without having prior knowledge of R.

Just before the turn of the millennium, the American Psychological Association (APA) Task Force on Statistical Inference recommended that “interval estimates should be given for any effect sizes involving principal outcomes” (Wilkinson, 1999, p. 599). This recommendation was adopted in subsequent editions of the Publication Manual of the American Psychological Association. For example, the current edition states that “complete reporting of . . . estimates of appropriate effect sizes and confidence intervals are the minimum expectations for all APA journals” (APA, 2009, p. 33). Reporting confidence intervals (CIs) for effect sizes is the current “best practice” in social science research (Cumming & Fidler, 2009; Kline, 2004; Steiger, 2004; Thompson, 2002). Even so, psychologists and other social scientists have been slow to include CIs in their research reports. Persistence by Geoffrey Loftus raised the percentage of articles that reported CIs in Memory & Cognition from 8 % to 45 % during his tenure as editor, but this fell to 27 % after his term ended (Finch et al., 2004). Finch et al. estimated that only about 22 % of published experimental psychological research includes CIs.

One hurdle for reporting CIs is that standard statistical software packages provide only rudimentary support for CIs. It is difficult for authors to follow the APA Task Force’s recommendation when the software that they know how to use will not compute CIs for all of their primary effects without the programming of specialized routines. Most standard programs compute CIs only for sample statistics or parameter estimates, such as means, and typically those CIs are computed using traditional methods that are known to have poor coverage (i.e., the proportion of randomly sampled CIs that contain, or cover, the fixed population parameter differs markedly from the purported confidence level).

Kelley (2007a, 2007b) made a major contribution to available software with the introduction of MBESS, an R package for generating exact CIs for some effect size measures (Kelley & Keke, 2012). Exact CIs on effect sizes are generated by finding the most extreme (upper and lower) population effect sizes whose theoretical cumulative probability distributions would yield the observed sample’s effect size with a total probability equal to the desired level of confidence. These upper and lower extremes are found using a computationally intensive iterative procedure. The routines in the MBESS package were based on those described by Steiger and Fouladi (1992, 1997) and Steiger (2004). When the underlying data are normally distributed, these CIs are exact, in that they represent the theoretical best estimates. However, as Kelley himself has shown, exact CIs are nonrobust to departures from normality (Algina, Keselman, & Penfield, 2006; Kelley, 2005). When the data are known not to be normally distributed or when the distribution is unknown (the most common situation for most research), a better approach is to use bootstrap CIs, which we describe in the next section.

Our purpose in this article is to illustrate usage of bootES (Bootstrap Effect Sizes; Gerlanc & Kirby, 2012), a free software package for R. We developed this package to make it easy for psychologists and other scientists to generate effect size estimates and their bootstrap CIs. These include unstandardized and standardized effect size estimates and their CIs for mean effects, mean differences, contrasts, correlations, and differences between correlations. Both between-subjects and within-subjects effect sizes, and mixtures of the two kinds, can be handled, as described below.

R is a free, open-source language and environment for statistical computing (R Development Core Team, 2012). It is rapidly increasing in popularity because of its price, power, and the development of specialized packages. R’s reputation for a “steep learning curve” is well deserved, partly because R’s thorough online documentation is written primarily by developers for developers. However, R is easy to use if one is shown how. In Appendix 1 and the supporting command files, we provide all of the R commands that a user would need to know to compute all of the CIs described in this article, from importing the data to saving the results. Thus, the reader can perform all of the analyses in this article without consulting any other R documentation. Over time, the reader may then begin to use some of R’s additional built-in functionality, such as its publication-quality graphics or any of the excellent packages that have been developed for psychological research, such as MBESS and the psych package (Revelle, 2012).

Bootstrap confidence intervals

Confidence intervals

Point estimates of effect sizes should always be accompanied by a measure of variability, and confidence intervals provide an especially informative measure (APA, 2009, p. 34). In this section, we provide a brief introduction to bootstrap CIs. For readers who wish additional background, we recommend Robertson (1991), Efron and Tibshirani (1993), and Carpenter and Bithell (2000) as good starting points.

A population parameter, θ, such as a population effect size, can usually be obtained from its corresponding sample statistic, $\hat{\theta}$. However, we also would like to know the precision of the estimate. What range of values of θ are plausible, given that we have observed $\hat{\theta}$? The range of plausible values is provided by a CI (Efron & Tibshirani, 1993), where plausibility is defined by a specified probability (typically, 95 %) that intervals of the type computed would cover the population parameter. (The “alpha-level,” α, is equal to 1 minus the desired confidence level expressed as a proportion; so, for a 95 % CI, α = .05. It gives the nominal proportion of samples for which CIs would fail to cover the population parameter.)

Finding a CI for $\hat{\theta}$ requires information about its population distribution—that is, the distribution of $\widehat{\theta}$ that one would obtain from infinite sampling replications. Unfortunately, this distribution often is unknown. To fill this void, traditional parametric CI methods start with an assumption about the shape of the population distribution. For example, it is common to assume that a population of sample mean differences is distributed as (central) t. However, this will be true only under the null hypothesis and when the population scores are normally distributed. In contrast, exact CI methods assume, more appropriately, that the population of mean differences is distributed as a noncentral t, with a population parameter equal to the observed difference. In both methods, the assumed theoretical distribution is used as the basis for constructing the CI around $\widehat{\theta}$. CI coverage performance depends on the appropriateness of the distributional assumptions, and it is often quite poor (DiCiccio & Efron, 1996).

Bootstrap methods

Bootstrap methods (Efron, 1979) approximate the unknown distribution of $\widehat{\theta}$ from the data sample itself. This is done by repeatedly drawing random samples (called resamples) from the original data sample. These resamples contain the same number of data points, N, as the original sample, and because the values are drawn with replacement, the same sample value can occur more than once within a resample. The desired statistic $\widehat{\theta}$ is calculated anew for each resample; denote each resample statistic ${{\widehat{\theta}}^{*}}$. If the number of bootstrap resamples (R) were, say, 2,000, then we would have 2,000 ${{\widehat{\theta}}^{*}}$s. The distribution of these ${{\widehat{\theta}}^{*}}$s serves as an empirical approximation of the population distribution of $\widehat{\theta}$, and we can use it to find a CI for $\widehat{\theta}$. Most simply, to find a 95 % CI, put the resampled values of ${{\widehat{\theta}}^{*}}$ in rank order and locate the values at the 2.5 and 97.5 centiles in the distribution. This is called a “percentile” bootstrap CI. Such intervals make no assumptions about the shape of the distribution of $\widehat{\theta}$.

Such simple percentile bootstrap CIs have an advantage in computational transparency, but they suffer from two sources of inaccuracy (DiCiccio & Efron, 1996; Efron, 1987). First, many sample statistics are biased estimators of their corresponding population parameters, such that the expected value of $\widehat{\theta}$ does not equal θ. Second, the standard error of an estimate of $\widehat{\theta}$ may not be independent of the value of θ; consequently, even for unbiased estimates, the lower and upper percentile cutoffs may not be the same number of standard error units from $\widehat{\theta}$ (DiCiccio & Efron, 1996, p. 194). The bias-corrected-and-accelerated (BCa) bootstrap method, which was introduced by Efron (1987), reduces both sources of inaccuracy by adjusting the percentile cutoffs in the distribution of the resampled ${{\widehat{\theta}}^{*}}$ for both bias and the rate of change, called the acceleration, of $\widehat{\theta}$ with respect to change in θ. The details of the BCa method are provided in Appendix 2.

The BCa method has two important properties that give it an advantage over other methods in many contexts (Efron, 1987). First, the CI coverage errors for the BCa method go to zero with increases in sample size N at a rate of 1/N, whereas the tail coverage errors for traditional and simple percentile bootstrap methods go to zero at the much slower rate of $1/\sqrt{N}$. This is one reason why BCa intervals outperform traditional and percentile bootstrap CIs in most applications. For both normal and nonnormal population distributions with sample sizes of roughly 20 or more, Monte Carlo research has shown that BCa intervals yield small coverage errors for means, medians, and variances (Efron & Tibshirani, 1993; Lei & Smith, 2003), correlations (DiCiccio & Efron, 1996; Lei & Smith, 2003; Li, Cui, & Chan, 2013; Padilla & Veprinsky, 2012), and Cohen’s d (Algina et al., 2006; Kelley, 2005). The magnitude of the coverage errors and whether they are liberal or conservative depend on the particular statistic and the population distribution, and BCa intervals can be outperformed by other methods in particular circumstances (see, e.g., Hess, Hogarty, Ferron, & Kromrey, 2007). Nevertheless, their relative performance is typically quite good, and they are recommended for general use in a wide variety of applications (Carpenter & Bithell, 2000; Efron & Tibshirani, 1993, p. 188).

A second important property of the BCa method is that, like the percentile method, it is transformation respecting. This means that for a monotonic transformation f of the statistic θ, the endpoints θ _low and θ _hi of the CI on θ can be transformed to find the endpoints f(θ _low) and f(θ _hi) of the CI on f(θ). This is important because the standardized effect sizes that are implemented in bootES that have not been studied directly are monotonic transformations of Cohen’s d (defined below), which has been studied extensively in Monte Carlo simulations. Thus, the coverage performance found in previous Monte Carlo results should hold for our other effect sizes as well.

The BCa method was implemented by Canty and Ripley (2012) in the boot.ci function in the R boot() package. BootES uses the boot.ci implementation of BCa as its default method. Other bootstrap methods are available as described in the General Options section below.

Limitations and sample sizes

Bootstrap CIs do not cure the problems of small sample sizes. Although BCa CIs may outperform traditional CIs for small samples from nonnormal populations (see, e.g., Davison & Hinkley, 1997, pp. 230–231), their coverage for small sample sizes can still differ substantially from the nominal 1 − α. This is because bootstrap CIs depend heavily on sample values in the tails of the sample distribution. The several smallest and largest resampled statistics will be computed from those resamples that happen to draw observations primarily from the tails of the distribution of sample values. For small samples, the tails are sparsely populated, so the percentile cutoffs could be determined by a very small number of sample values. The more extreme the confidence level (i.e., the smaller the α), the more the cutoff will be determined by a small number of extreme sample values. The BCa method can exacerbate the problem because the adjusted cutoffs may move even further into the tails of the distribution. When this is a problem, increasing the sample size and the number of bootstrap resamples can improve coverage.

Monte Carlo simulations of BCa bootstrap CIs have been conducted for a wide variety of statistics. Here, we briefly summarize four of these to provide a sense of BCa CI coverage in small samples. Kelley (2005) found excellent coverage in Monte Carlo simulations of BCa intervals across a range of population distributions of Cohen’s d; for sample sizes of n ₁ = n ₂ = 15 or more, coverage probabilities for 95 % CIs ranged from 94.1 % to 96.5 %. For example, for the difference between the means of two normal distributions with equal means and variances, the coverage probability was 95.96 % (Kelley, 2005, Table 1). Algina et al. (2006) also found very good coverage for Cohen’s d when n ₁ = n ₂ = 25, for all but their most nonnormal populations. (Notably, Algina et al. [2006] refrained from simulating smaller samples because they “wanted to avoid encouraging the use of small sample sizes.” (p. 948)) Davidson and Hinckley (1997, Table 5.8) computed the ratio of two means, each drawn from different gamma distributions, which had a highly nonnormal population distribution. They observed a respectable 93.2 % coverage for 95 % BCa intervals when n ₁ = n ₂ = 25. Finally, for nominal 99 % CIs, Carpenter and Bithell (2000, Table IV) observed a 98.94 % coverage rate for BCa intervals on means drawn from an inverse exponential distribution (a moderately nonnormal distribution) when n = 20. However, with a sample size of n = 5, the error rate was more than 1.8 % just in the upper tail alone.

As a consequence of these and other simulation results, for 95 % BCa CIs, we recommend sample sizes of approximately 20 or more in each group. To be safe, larger sample sizes, or robust effect size estimates (Algina et al., 2006), should be considered when (1) the distribution of sample values is strongly nonnormal, (2) a smaller α is desired, such as for a 99 % CI, and the distribution of sample values is noticeably nonnormal, or (3) the effect size is large (and therefore may have arisen from a nonnormal distribution of population effect sizes).

Number of resamples

Bootstrap methods are computationally intensive in that they require a large number of resamples and calculations. When these methods were being developed in the 1980s, the computing time required to generate several hundred resamples was substantial, and some effort was devoted to determining the smallest number of resamples that could yield adequate CI coverage (e.g., Hall, 1986). For a 90 % CI, Efron and Tibshirani (1993) recommended that the number of resamples should be “≥ 500 or 1000” (p. 275). Davison and Hinkley (1997) said that “if confidence levels 0.95 and 0.99 are to be used, then it is advisable to have [the number of resamples] = 999 or more, if practically feasible” (p. 202). Today, such numbers take only seconds, and it is practically feasible to use much larger numbers of resamples. In bootES, we have implemented a default of 2,000 resamples, but users may change this number as described in the General Options section below.

Comparison with other software

To our knowledge, bootES is the only software that implements bootstrap CIs for all of the effect sizes and data structures described below without requiring users to write specialized code. BootES makes use of the bootstrapping implementations in the boot() package, which was originally written for S-Plus by Canty (2002) and was later ported to R by Ripley (Canty & Ripley, 2012). The boot() package is extremely flexible in that it can perform bootstrap resampling for any user-defined function that is written for a particular data structure. Thus, boot() is not constrained to the statistics or data structures described below. However, beyond the simplest cases, writing appropriate functions for use with boot() is not trivial. The advantage of using bootES is that the effect size functions are built in for the types of data structures commonly used by social scientists. BootES contains optional arguments to control those built-in functions, but in typical applications, bootES keeps the number of user-specified options to a minimum by making use of the structure of the data to help select the appropriate effect size function.

Bootstrapping methods are becoming more widely available, and all of the major commercial statistical programs provide their own scripting languages, which allow users to write their own functions and programs. Thus, users who know those scripting languages could write programs to perform any of the computations described below. However, no commercial software offers the breadth of bootES’s built-in effect size measures and their bootstrap CIs. SYSTAT (version 13), JMP Pro (version 10), and the bootstrapping add-on module for IBM-SPSS (version 20) allow users to compute bootstrap CIs for the summary statistics and parameter estimates computed by many of their procedures. SAS (version 9) provides a customizable bootstrapping macro, but the user needs to know how to program in the SAS macro language. Stata (version 12) has a bootstrap command that allows the user to find bootstrap CIs for user-defined functions of the saved results of existing commands. Resampling Stats (version 4) offers Microsoft Excel and Minitab add-ins that compute bootstrap CIs for user-defined functions. Users already familiar with a commercial program might find that its bootstrapping capability meets their needs. If not, bootES offers “one stop shopping” in a free package.

Example data

To illustrate each type of analysis below, we will use the example data shown in Table 1. (This is a toy data set for illustration purposes; we do not mean to encourage the use of such small sample sizes.) A text file containing these data is provided with the bootES package and can be imported using the command shown in Appendix 1. Users without access to the data file may enter the data in a spreadsheet and save it as a comma-separated-value (csv) file; once the csv file exists, it can be imported into R in the normal manner as described in Appendix 1. (Readers who are new to R may wish to read Appendix 1 before continuing to the next section.) In R, the imported data will be contained in an object called a data frame, and the data frame must be given a name by the user. In the import command described in Appendix 1, we called our example data frame “myData,” and we used that name throughout our examples.

Table 1 Example data, contained in the data frame “myData”

To illustrate the use of units of measurement below, let’s pretend that Dosage is measured in milligrams and that the three dependent measures (“Meas1,” “Meas2,” and “Meas3”) are task completion times in seconds.

CIs for means and general options

BootES provides a variety of options that allows the user to customize the type of CI and output. In this section, we illustrate some of these options with CIs on means. In most instances, users can simply omit these options and use the default values. As in the R console, all R commands and output are shown below in Monaco font. Where long commands or output cut across columns, a horizontal line in the left column indicates that the text shifts to the right column; after the command or output, the text shifts back to the left column.

CIs on means

When a single variable name (a single column of numbers) is given as an argument, bootES will find the mean and 95 % bootstrap BCa CI for that variable. Suppose, for example, that we wish to find the CI for the grand mean of measure 1 (“Meas1”) in myData. This column can be picked out using standard R notation—in this instance, “myData$Meas1” (see Appendix 1 for an explanation of this notation). To execute a command in R, simply type (or paste and edit) the command after the “>” prompt in the R console and press return. The mean can be found with the R command:

To find the CI for this mean, we could type

We can also omit the “data=” part, so long as the data name appears in the first argument to bootES. We do this in all of the example commands below. Thus, a simpler command is

Executing this command results in output like this:

The mean of measure 1 is 269.95 s, with a 95 % CI from 228.72 to 315.79 s. These values can be copied from R and pasted into, say, the results section of a manuscript. The bias, 0.028 s, is the difference between the mean of the resamples and the mean of the original sample. The “SE” is the standard error—that is, the standard deviation of the resampled means.

Above, we said “output like the following” because bootstrap resampling involves taking repeated random samples of one’s data, so these intervals will be slightly different each time. Readers who wish to replicate our numbers in this article exactly may do so by executing the command set.seed(1) immediately before each use of the bootES function. This command resets the seed of R’s random number generator.

General options

Number of resamples

As was discussed above, by default bootES resamples the data 2,000 times. This can be changed using the option “R =,” followed by the desired number of resamples. For example, to find the 95 % CI for measure 1 based on 5,000 resamples, the command would be

The difference between these estimates and those for “R = 2,000” were small in this instance. The difference in computing time was also negligible (on a 2.93-GHz computer, 2,000 replications took 0.065 s and 5,000 replications took 0.147 s).

Confidence level

The default confidence level for CIs in bootES is 95 %. This level can be changed using the “ci.conf” option. For example, to find the 99 % CI for the mean of measure 1, use

As was expected, this CI is wider than the 95 % CI above.

CI method

As was discussed above, bootES uses by default the BCa method for computing bootstrap CIs, which has been shown to have excellent coverage in a wide range of applications. We recommend that readers use this method unless there is reason a priori to think another method would be superior for a particular data set. In such a case, the other methods offered by the R boot package (Canty & Ripley, 2012) are also available as options: “basic,” percentile (“perc”), normal approximation (“norm”), and studentized (“stud”). (Note that the studentized method requires specification of bootstrap variances as an argument; see the boot.ci help page in R for more information on that option.) These methods are described in Davison and Hinkley (1997, Chap. 5). (The option “none” is also available if one wishes to generate plots of resampled values without computing CIs.)

To illustrate, if one wished to use the normal approximation method to find the CI for the mean of measure 1, set the option “ci.type” to “norm”:

Plots

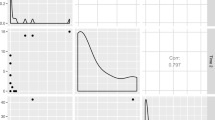
Behind the scenes, the boot() function creates an object that contains the resampled statistics along with plotting information. As with boot(), bootES users may save this object under some arbitrary name—for example, myBoots = bootES(…)—and then extract the resampled statistics or pass this object by name as an argument to the plot function to generate a histogram and Normal quantile-quantile plot of the resampled statistic. Alternatively, in bootES, one can easily generate these plots using the option “plot = TRUE.”

The numerical output will be the same as in our first example above, but the desired plots will be generated in a graphics window. The plots for this example are shown in Fig. 1 and indicate that the resampled means are approximately normally distributed.

Fig. 1

For 2,000 resampled means of example measure 1 (labeled “t*” by default), the left panel shows the histogram, and the right panel shows the Normal quantile-quantile plot

Between-subjects (group) effect sizes

In many instances, effects are defined across group means. Because subject is typically a random factor, resampling methods must randomly resample subjects within groups, while respecting the number of subjects in each group in the original sample. This properly simulates the uncertainty in the estimate of each group mean, and it is the resulting unweighted resampled means that bootES uses to estimate an effect size between groups. Thus, bootES provides unweighted-means effect sizes, which are appropriate for most scientific questions (Howell & McConaughy, 1982).

Between-subjects: Unstandardized effect size measures

An unstandardized effect size measure is one that expresses the size of an effect in units of measurement—typically, the original units of measurement in the research. For example, a study that measures response times in milliseconds might report the size of the observed effects in milliseconds. These effect sizes are useful primarily when the original units are meaningful and readily interpretable by readers.

Contrasts

A contrast, also called a comparison of means (Maxwell & Delaney, 2004), is a linearly weighted combination of means, defined for a sample as

$$ C=\sum {{\lambda_j}{M_j}} :\sum {{\lambda_j}=0}, $$

(1)

where the M _j are the sample estimates of the population group means μ _j . Each mean is multiplied by its corresponding contrast weight, λ _j , and the sum of the λ _j must be zero. The sign of C indicates whether the pattern in the group means is in the direction predicted by the contrast weights (+) or in the opposite direction (−).

Two groups

For a difference between two means, the λs in Eq. 1 are simply +1 and −1. In bootES, the user must specify the groups that are involved in the contrast using the “contrast” option, wrapped within R’s c() function (concatenation). Each group label is followed by an equal sign and its contrast weight. For example, to find the difference between the means of females and males, one could use the option “contrast = c(female = 1, male = −1).” As a convenience, when only two groups are involved in the contrast, the user may omit the contrast weights but add single or double quotes—for example, “contrast = c(‘female’, ‘male’).”

We must also tell bootES which column contains the “data” (the dependent, or outcome variable) and which column contains the grouping variable (the independent, or categorical predictor variable). These are specified using the “data.col” and “group.col” options, respectively. For example, suppose we wish to find CIs for the mean difference in measure 1 between females and males in the example data set. In this case, the group.col is “Gender” and the data.col is “Meas1.” Pulling these options together, we use the following command:

Note that the command was lengthy and wrapped onto a second line. That makes no difference in R; all input prior to pressing the return key will be interpreted as part of the same command.

The means of the groups can be found easily using a built-in R command, by(), which finds a statistic “by” groups. The first argument is the data column, the second argument is the grouping column, and the third argument is the desired statistic:

Three or more groups

All else being equal, a contrast increases with an increasing correspondence between the pattern in the contrast weights and the pattern in the means. Consequently, a raw contrast C may serve as a measure of effect size. However, the magnitude of C is also affected by the arbitrary scaling of the choice of weights, so the choice of weights can affect the reader’s ability to interpret the contrast as an effect size. Therefore, when reporting an unstandardized contrast as an effect size measure, it is important to choose contrast weights such that they preserve the original units of measurement (or at least some nonarbitrary unit). This can be accomplished by making the positive contrast weights sum to +1 and the negative contrast weights sum to −1. The contrast can then be interpreted as a difference between two weighted means (i.e., weighted by contrast weights), and it will express the effect in the original units of measurement of the dependent variable.

To illustrate, suppose we wish to assess the increase in measure 1 in the example data—task completion time measured in seconds—as a linear function of dosage condition. The three conditions, A, B, and C, in the example data correspond to dosages of 30, 60, and 120 mg, respectively. To find linear contrast weights, we can simply subtract the mean of these dosages from each dosage. The mean is (30 + 60 + 120)/3 = 70, so the corresponding contrast weights are 30–70 = −40, 60–70 = −10, and 120–70 = 50, respectively. Using the labels for the variable condition within the data frame, our contrast specification becomes “contrast = c(A = −40, B = −10, C = 50).” These contrast weights capture the same effect as would, say, the weights (−4, −1, 5), but the former will lead to an unstandardized effect size 10 times as large as the latter for the same data. To express C in the original units of measure 1, the weights must be scaled to (−0.8, −0.2, 1). This scaling of contrast weights is done by default in bootES, for any weights provided by the user. Both the original and scaled lambda weights are reported in the output:

The value of C, 61.44 s, is in the original units of measure 1. Weight scaling can be overridden by the user with the option “scale.weights = FALSE.”

Slopes

A special case of a linear contrast is one that gives the slope of the relationship between the outcome variable and the predictor variable. A slope expresses the linear relationship as numbers of unit change in the outcome variable per one unit change in the predictor variable, in the original units of measurement. For example, if one’s hypothesis predicted a linear increase in mean task completion time (in seconds) as drug dosage increased across three drug dosage conditions (e.g., 30, 60, and 120 mg), one might wish to express the effect, with its associated CI, as a slope with units s/mg. This can be accomplished by scaling the contrast weights appropriately. One obtains each scaled weight by demeaning the values, X, on the predictor variable (e.g., dosages) and then dividing each by the sum-of-squares (SS) of those values:

$$ {\lambda_j}=\frac{{{X_j}-\overline{X}}}{{\sum {{{{\left( {{X_j}-\overline{X}} \right)}}^2}} }}. $$

(2)

This is done automatically in bootES when the “slope.levels” option is used instead of the “contrast” option.

To illustrate, suppose one’s grouping variable is nonnumeric (e.g., conditions A, B, and C), but one knows their corresponding numeric values (e.g., 30, 60, and 120 mg). As with contrasts more generally, the mapping of group labels and numeric values (A = 30, B = 60, C = 120) can be given in the “slope.levels” argument, and the appropriate slope weights will be used:

The observed slope is 0.73 s/mg, with a 95 % CI from −0.47 s/mg to 1.88 s/mg.

Alternatively, when the grouping variable designated by “group.col” is numeric, those numeric values will be used as levels of the predictor variable. For example, the 30-, 60-, and 120-mg dosage levels are contained in the “Dosage” column of myData, which can be specified in the slope.levels option:

The output would be identical to that in the previous example.

Between-subjects: Standardized effect size measures

It is often preferable to report standardized, or “scale-free” measures of effect size. Such unitless measures can be meaningful to readers even when they have little intuitive understanding of the effects in the original units. Standardized measures also allow easier assessment and combination in meta-analyses (Glass, 1976; Hedges & Olkin, 1985). We have implemented several standardized effect size measures in bootES.

Cohen’s d-type effect size measures

One approach to standardizing an effect size is to express the effect in standard deviation units. Typically, this means dividing the unstandardized effect size by an estimate of the population standard deviation. Such effect sizes, including the four in this section, are variations on what is typically called “Cohen’s d,” after Cohen (1969).

Cohen’s δ and d

Cohen (1969) was concerned primarily with using guesses about population effect sizes to estimate the power of significance tests and with estimating sample size requirements for achieving desired levels of power. Consequently, he defined his effect size measures in terms of population parameters. For the difference between two means, the effect size is found by

$$ \delta =\frac{{{\mu_A}-{\mu_B}}}{\sigma }, $$

(3)

where μ _A and μ _B are population means of groups A and B, expressed in original units, and σ is the population standard deviation common to the two groups (see Cohen, 1969, p. 18, Eq. 2.2.1). That is, σ is $\sqrt{{{{{\left( {S{S_A}+S{S_B}} \right)}} \left/ {{\left( {{n_A}+{n_B}} \right)}} \right.}}}$, where SS _j is the sum of squares and n _j is the number of sample values for group j. (Although Cohen, 1969, denoted this quantity with the Latin d, we use the Greek δ because Eq. 3 represents a population parameter.) For a single mean effect, expressed as a standardized difference between that mean and some theoretical value (perhaps zero), the definition is obtained by substituting the theoretical value for μ _B and using $\sigma =\sqrt{{{SS \left/ {n} \right.}}}$ in Eq. 3.

The population parameter form in Eq. 3 is useful for those who wish to use Cohen’s (1969) power tables or when one wishes to view the size of the effect relative to the standard deviation of the sample itself (Rosenthal & Rosnow, 1991, p. 302). We make this variation available in bootES with the option ‘effect.type = “cohens.d.sigma”.’ For example, for the difference between the measure 1 means for males and females in the example data set,

The gender difference in original units of measure 1 was 48.7 s. Is that large or small? The standardized effect size tells us that the difference is about half a standard deviation (0.50σ), with a 95 % bootstrap CI from −0.52σ to 1.51σ.

Outside the context of a priori power calculations, such as when one is estimating the standardized effect size from data, it is usually more appropriate to divide the unstandardized effect size by an unbiased estimate of the population standard deviation. An unbiased estimate is obtained from the pooled standard deviation of scores (denoted s, S, or $\widehat{\sigma}$) and requires use of the familiar “n − 1” formulas for computing the standard deviation. For two groups, the pooled estimate of the standard deviation is $s=\sqrt{{\left( {S{S_A}+S{S_B}} \right)/\left( {{n_A}+{n_B}-2} \right)}}$. Thus, the difference between two group means in standard deviation units is given by

$$ d=\frac{{{M_A}-{M_B}}}{s}, $$

(4)

where M _A and M _B are the sample means of the two groups. For a single mean effect, expressed as a standardized difference from some theoretical value, the definition is obtained by substituting the theoretical value for M _B , and using $s=\sqrt{{{SS \left/ {{\left( {n-1} \right)}} \right.}}}$ in Eq. 4. We will return to single means as effect sizes in the section on within-subjects effects below.

The quantity in Eq. 4 is often called “Cohen’s d,” d′, or simply d (Cumming & Finch, 2001; Hunter & Schmidt, 1990; Killeen, 2005), despite its having a different denominator than Cohen’s (1969) original “d,” in Eq. 3. This varied usage is understandable, since even Cohen implied that values of d used for power calculations sometimes would be based on estimates of σ (e.g., Cohen, 1969, p. 39).

We have made the effect size in Eq. 4 available in bootES using the option “cohens.d.” Returning to our previous example of the effect size for the difference in the mean of measure 1 between females and males, the value of Cohen’s d and its CI can be found by

Hedges’s g

Although Eq. 4 uses an unbiased estimate of σ, d is not an unbiased estimate of δ but tends to be a little too large (Hedges, 1981). Hedges derived an unbiased estimator of δ, which he denoted g ^U (Hedges, 1981, Eq. 7), apparently named after Glass (1976). This has come to be known as “Hedges’s g,” and it is defined as

$$ g=d\frac{{\Gamma \left( {\frac{df }{2}} \right)}}{{\sqrt{{\frac{df }{2}}}\Gamma \left( {\frac{df-1 }{2}} \right)}}, $$

(5)

where d is defined as in Eq. 4, df is the degrees of freedom used to compute s in Eq. 4, and Γ is the Euler gamma function. The correction factor—the fraction on the right side of Eq. 5—is always less than 1 but approaches 1 rapidly as df increases.

Returning to our previous example of the effect size for the difference in the mean of measure 1 between females and males, the value of Hedges’s g and its CI can be found by

As was expected, the value of Hedges’s g is slightly smaller than the value of Cohen’s d found above.

When the goal is to estimate δ from empirical data, Hedges’s g is preferable to the traditional Cohen’s d. On the basis of his Monte Carlo simulations, Kelley (2005) recommended using Hedges’s g (which he denoted d _u ) in conjunction with BCa intervals.

Glass’s ∆

In some contexts, it may be desirable to express an effect across groups, relative to the standard deviation of scores in a single group, such as a control group (Glass, 1976; McGaw & Glass, 1980; Smith & Glass, 1977). This is sometimes called Glass’s ∆ (McGaw & Glass, 1980; Rosenthal, 1984). We provide this option for Eqs. 3, 4, and 5, with the optional argument ‘glass.control = “[group label]”.’ Typically, one will want to use Hedges’s unbiased version in Eq. 5, as illustrated here:

Robust d

The foregoing variations on Cohen’s d are not robust statistics, in that small changes in the population distribution can strongly affect their values (Wilcox & Keselman, 2003). Robust statistics are preferred, for example, when one is trying to control type I error in the context of null hypothesis significance testing. Algina, Keselman, and Penfield (“akp”) (2005) proposed a robust version of Cohen’s d, which they denoted d _R. They replaced the means in Eq. 4 with 20 % trimmed means (i.e., the mean of the middle 60 % of the data) and replaced s with a 20 % Winsorized standard deviation, which is scaled (divided by 0.642) to ensure that it is a consistent estimator of σ when the distribution is normal. This robust variation is available in bootES using the option ‘effect.type = “akp.robust.d”.’ Here is its value and CI for the difference in the mean of measure 1 between females and males:

Algina et al. (2005, 2006) showed that bootstrap CIs provided excellent coverage for d _R with as few as 20 subjects per group, even with strongly nonnormal distributions and δ _R as large as 1.40.

Note that the interpretation of d _R is different than that of d. A 20 % trimmed sample mean estimates a 20 % trimmed population mean—the mean of the middle 60 % of the population—whereas an untrimmed sample mean estimates the population mean of the whole distribution (Wilcox & Keselman, 2003). Consequently, d _R measures the difference between the middle 60 % of the groups, in units of the standard deviation of the middle 60 %. Whether this is the effect size of interest depends on one’s scientific question.

Standardized contrasts

Although variants of d are most often used to express differences between means, or between means and theoretical values, they can equally well be used to express the standardized magnitudes of other types of contrasts (Steiger, 2004; Steiger & Fouladi, 1997). The expression for a standardized contrast is a generalization of Eq. 4,

$$ {d_C}=\frac{{\sum {{\lambda_j}{M_j}} }}{s}, $$

(6)

where the λs express a quantitative hypothesis and sum to zero, as in Eq. 1. The sign of d _C indicates whether the pattern in the group means is in the direction predicted by the contrast weights or in the opposite direction.

A subtle issue arises in this context: To create a scale-free effect size, expressed in standard deviation units, the contrast (the numerator) must be computed with weights that preserve the original units, as shown in Eq. 2, so that the numerator and denominator in Eq. 6 will have the same units and those units can be canceled. This scaling of contrast weights is performed by default in bootES wherever there are more than two groups involved in the contrast and one of the d-type effect sizes is requested.

For a d-type standardized effect size for a contrast, as for a difference between two means, one would typically want to include the bias correction in Eq. 5. To illustrate both weight scaling and bias correction, here is Hedges’s g for the example from the previous section on contrasts:

Note that the contrast weights, −40, −10, and +50, were rescaled to −0.8, −0.2, and +1. The value of g = 0.57 is an unbiased estimate of δ for the contrast and indicates that the contrast—in this case a linear trend—was a little over a half standard deviation in magnitude in the direction predicted by the contrast weights.

Pearson’s r

An alternative to Cohen’s d-type effect sizes for standardizing an effect is the Pearson correlation coefficient, r (Pearson, 1896). In the context of assessing mean effects, mean differences, and contrasts more generally, r can be interpreted as the partial correlation between the contrast weights and scores on the outcome variable, after having removed the group differences other than those associated with the contrast (Rosnow, Rosenthal, & Rubin, 2000). One benefit of expressing an effect size for a contrast as r is that it scales the effect to have an absolute magnitude between 0 and 1, with the sign indicating whether the trend in the group differences was in the direction predicted by the contrast weights or in the opposite direction.

For computing r for a contrast directly from the data, bootES uses the following equation:

$$ {r_{contrast }}=\frac{C}{{\sqrt{{{C^2}+S{S_p}\sum {\frac{{\lambda_j^2}}{{{n_j}}}} }}}}, $$

(7)

where SS _p is the pooled within-group sum of squares, the n _j are the numbers of cases within each group, and C and λ are defined as in Eq. 1. (This is algebraically equivalent to computing r from a t-test of a contrast as illustrated in Rosnow et al., 2000.) For a single mean effect, M, Eq. 7 simplifies to $r=M/\sqrt{{{M^2}+S{S_p}/n}}$.

Note that the scale of the contrast weights does not affect r, because the weights appear in both the numerator and denominator of Eq. 7. Thus, any convenient weights that capture one’s hypothesis and sum to zero may be used (although bootES scales them anyway). Here is the CI on the effect size r for the contrast from the previous section, which is generated using the ‘effect.type = “r”’ option:

Factorial between-subjects designs

The most transparent and least problematic way to analyze factorial designs is to treat the cells in such a design as though they were levels in a single-factor design (i.e., as in a one-way ANOVA). This approach can be used with bootES to test contrasts that are defined over any combination of cells in the factorial design. All contrasts of interest, their standardized effect sizes as defined above, and their CIs can be computed just as they were illustrated in the foregoing section on between-subjects effects.

To accomplish this, when the levels of multiple independent variables are contained in different columns in a data frame, those levels must be collapsed into a single column. It is easy to collapse manually two or more independent variables into a single variable using R’s paste() command, which takes the condition labels from the existing columns, joins them together, separated by a character that we specify, and stores the new cell labels in a new column. To illustrate, the data set in Table 1 has columns for gender (two groups) and condition (three groups). To paste their labels together into a new column with six groups, called, say, “GenderByCond,” we can use

Type “myData” at the prompt to see the new column in the R console. All contrasts that would be available in a factorial analysis can now be computed on this new, single factor, using the bootES methods described above.

However, as the number of levels or factors increases, specifying contrast weights at the level of the smallest cell in the factorial design can become cumbersome. For example, to compare the means of females and males in the factorial design gender × condition, using the methods described above, we could write

(Note that the value for the gender difference, 36.78 s, is different from the value in the earlier example because, here, it is computed across the unweighted means of the six conditions.) To avoid these redundant contrast weight specifications, as a convenience, we have included an option in bootES that allows a blocking column to be specified separately from the grouping column over which the contrast weights are defined. When blocking on only one other factor, such as blocking on condition in myData, this factor can be specified in the block.col option:

When the design has three or more factors, use the paste function to create a new column that defines the smallest cells, as we did above to create GenderByCond, and use that column as the blocking column.

Using the column that defines the smallest cells as the grouping column, such as GenderByCond, allows us to define contrasts over any combination of simple, main, and interaction effects. For example, the difference between the mean of females in condition A and the means of males in conditions B and C can be found by

Some readers may think it a disadvantage of this approach to factorial analysis that one does not get all of the standard main effects and interactions automatically, as one typically does in factorial ANOVA. However, factorial ANOVA also has disadvantages: (1) Many effects in the output of a factorial ANOVA are not of interest, but their inclusion raises type I error rates; (2) not all effects of interest are automatically included in factorial output but must be tested with contrasts; and (3) effects in factorial outputs are often “omnibus” (multi-df) effects that must be followed by post hoc contrasts anyway. A discussion of these problems can be found in Rosenthal and Rosnow (1991, pp. 467–469, 486).

Within-subjects (repeated measures) effect sizes

CIs for within-subjects effects must be computed in two steps. First, outside bootES, find a single number for each subject that defines the effect for that subject. In some instances, these might be effects that were directly measured by the measuring instrument. In other instances, the effects will need to be calculated from repeated measurements obtained from each subject. These include mean differences (also called “difference scores,” “change scores,” or “improvement scores”) or, more generally, within-subjects contrast scores (Rosnow et al., 2000, pp. 128–130). These scores must be in a single column in the data frame, and the mean of this column provides the mean unstandardized effect size across subjects. Second, use bootES to find the desired effect size measure and its bootstrap CI across subjects, just as one would do for completely between-subjects effects.

Within subjects: Unstandardized effect size measures

To illustrate, suppose we wish to find the CI for the mean change from measure 1 to measure 3 in the example data. The first step is to create a new column of numbers containing the difference score for each subject. Simply affix any new (unused) variable name, such as “M3minusM1,” after the data frame name and dollar sign, and set it equal to the difference:

R finds the difference for each subject and stores it in the new column in the data frame. For example, the first subject in Table 1 has a difference score of 264–212 = 52. (Type “myData” and press return in the R console to view the current data frame, including the new column.) We can now find the mean difference score with its 95 % CI in the same manner we did in the section on the CI for a single mean:

This method can be generalized to any within-subjects contrast. First, a contrast score is generated for each subject using Eq. 1, but with the subject’s score in each condition replacing the means (M _j ) in that equation. For example, if our hypothesized effect was that the mean of measures 1 and 2 would be less than measure 3, we could use the weights −0.5, −0.5, and +1 for each subject’s scores on measure 1, measure 2, and measure 3, respectively. Affix a new variable name, such as “M3vM1M2,” after the data frame name and dollar sign and set it equal to the contrast:

This command creates a new column of contrast scores that indicate the size of this unstandardized effect for each subject. For example, the first subject in Table 1 has a contrast score of (−0.5) * 212 + (−0.5) * 399 + (1) * 264 = −41.5. The mean of this column of contrast scores gives the mean effect predicted by the contrast across subjects, and its CI can be found in the same way as for the mean of any column of numbers:

Because within-subjects contrast scores are computed outside and prior to using bootES, the scale.levels option in bootES will have no effect on them. If one wishes to scale the weights to preserve the original units for an unstandardized contrast, one must choose appropriate weights oneself, such that the negative weights sum to −1 and the positive weights sum to +1, while preserving their relative sizes. (The weights −0.5, −0.5, and +1 did this in the example above.) Alternatively, one may use standardized effect sizes, as described next.

Within subjects: Standardized effect size measures

To find the standardized effect size for a mean difference or contrast within subjects, create the column of contrast scores using the method described in the previous section. (Because the effect size will be standardized, the scaling of contrast scores will make no difference, so any convenient weights that capture one’s hypothesis and sum to zero may be used.) Then specify the desired type of standardized effect size using the effect.type option in bootES. In this context, bootES will use a single-mean version of the standardized effect sizes defined above (i.e., Eqs. 3, 4, or 7 or robust d). For example, for the contrast in the previous section comparing the mean of measure 3 to the means of measures 1 and 2, one might wish to express the effect predicted by the contrast in standard deviation units using Hedges’s g:

The standardized mean contrast score, 0.52, indicates that the mean within-subjects difference between measure 3 and the means of measures 1 and 2 was about half a standard deviation in magnitude (because subjects is a random factor, the relevant standard deviation, and the one used by bootES, is the standard deviation of the contrast scores).

Mixed factorial designs

Often, as in the example data shown in Table 1, an experimental design contains both between-subjects factors (e.g., gender and condition) and within-subjects factors (e.g., measures 1, 2, and 3). For such mixed-effects designs, bootES requires a two-step approach. First, the within-subjects (repeated measures) factors are converted into a single column of contrast scores that correspond to the predicted within-subjects effects, as described in the section on within-subjects effects. Second, this column of contrast scores is then treated as the dependent variable in a completely between-subjects contrast analysis, as described in the section on between-subjects effects. These between-subjects contrasts examine how the within-subjects effects vary across groups. The various effect size measures are defined exactly as they were for between-subjects-only effects above.

To illustrate, in a previous example we created a new column in myData, “M3minusM1,” containing the within-subjects change scores from Meas1 to Meas3. It turns out that the mean change was large for females and nearly zero for males. To find the CI for the between-subjects gender difference in the size of this within-subjects change, we use the column of change scores as the data column, block on condition, and compute the contrast for the gender difference.

Females’ change scores were 130.2 s greater than those for males, on average, with a 95 % BCa bootstrap CI from 34.7 to 239.8 s.

In summary, in mixed factorial designs, we recommend that users reduce the repeated measures to nonrepeated measures by computing within-subjects contrast scores and then reduce the factorial between-subjects design to a single between-subjects factor, on which between-subjects contrasts and their CIs can be estimated in bootES. We believe that widespread adoption of this approach would result in a general improvement in data-analytic practice with factorial designs and lead to better scientific inferences than does the automatic generation of the full output from mixed factorial ANOVAs.

Correlations

BootES provides a convenient way of finding bootstrap CIs for a simple correlation between two variables and for between-group differences in correlations. When two columns of data are supplied to bootES with no grouping variable, by default, bootES computes the correlation between those two columns and finds the BCa bootstrap CI. Two columns can be picked out of a data frame using R’s built-in notation (see Appendix 1). Here is the correlation between measures 2 and 3 in the example data, using R’s built-in correlation function:

To find the bootstrap CI for this correlation, simply submit the two columns to bootES:

When a third column with exactly two group labels is submitted as a grouping variable, bootES computes the difference between the two groups in the size of the correlation. For example, we can find the gender difference in the correlation between measures 2 and 3:

Partial correlations, differences between correlated correlations, and other multivariate estimates are not currently implemented in bootES.

Conclusion

BootES is a free package that offers a combination of features that we do not believe currently exists in any other single piece of software. Most important, it computes bootstrap CIs for both standardized and unstandardized effect sizes for contrasts and performs scaling of unstandardized effect sizes to retain the original units of measurement. By making use of the structure of the data to help choose the appropriate built-in effect size function, bootES is able to do most of this with a single command and a small number of option specifications. Among its disadvantages are that bootES is command-line driven and requires the use of R, which is not particularly user-friendly. However, by providing copy-paste-edit examples of command lines in this article and an overview of R in Appendix 1, we hope we have mitigated these disadvantages.

Our goals in creating bootES were to help researchers fulfill the APA’s requirement of “complete reporting of . . . estimates of appropriate effect sizes and confidence intervals” (APA, 2009, p. 33) and, thereby, to embolden more researchers to begin the transition away from null hypothesis significance testing (Harlow, Mulaik, & Steiger, 1997). When the population distribution is believed to be normal, perhaps on the basis of bootstrap data such as that shown in Fig. 1, we recommend that researchers report exact CIs for one of the effect sizes available in MBESS (Kelley & Keke, 2012). When the population distribution is known not to be normal or unknown, which is the more common situation, we recommend that researchers use bootES to report BCa bootstrap CIs for one of the effect sizes described above.

Appendices

Appendix 1

In this Appendix, we provide readers with (just) enough information on the basics of R to enable them to conduct the analyses described in this article. Official R documentation can be found at http://cran.r-project.org/manuals.html. Venables and Smith (2012), available at that Web site, is an authoritative and accessible introduction. A large number of user-provided guides can be found at http://cran.r-project.org/other-docs.html.

Downloading and installing R

R may be downloaded free of charge for Windows, Mac OS, and Linux operating systems from http://cran.r-project.org/mirrors.html. After selecting a mirror site close to one’s region, simply click on the link for the precompiled binary distribution appropriate for one’s operating system. Follow the instructions for downloading and installation.

Commands in R

R is an interpreted programming language. The standard R package comes with a rudimentary graphic user-interface with several menu options, but we recommend using commands for cross-platform consistency. To execute a command, simply type the command after the “>” prompt in the R Console and press return or enter. R interprets the command, and if it knows how, it carries out the command. When commands exceed the width of the R console, they will wrap onto additional lines, but this will make no difference in how R interprets the command; all input prior to pressing the return key will be interpreted as part of the same command.

To minimize typing, commands can be copied and pasted from a text file and then edited or imported from a command file. All of the commands in this article can be found in file “commands.txt,” which is bundled with the bootES package and can be obtained by typing

This command will put the file in the/bootES/inst directory on the users’ computer.

Installing and loading the bootES package

In addition to the R program itself, to use the functions in this article, one must also download and install bootES. At the R command line, simply type the following command on a computer with an Internet connection:

(If you forget the command, you can also perform the download from the Packages & Data/Package Installer menu item.) Installation need only be done once on each computer.

However, every time you restart R and wish to use the bootES library of functions, you will need to load the package. To do so, you can use the Packages & Data/Package Manager menu item, or simply type

Our bootES package depends on another R package called “boot.” That package must also be installed and loaded. This will happen automatically when you install and load bootES.

Importing data

The data entry and editing capabilities of current versions of R are quite limited. We recommend entering data into spreadsheet software, or other statistical software that one is already using, and then saving the data file as a comma-separated values (.csv) file. The data should have a typical row and column format, where the rows are separate subjects or cases and the columns are variables. It is best to save the column (variable) names as the first row in this file, if possible, because adding the names in R later would require additional, tedious steps.

For a file with the row–column structure described above, data may be imported into R with the command

This will store the data in R in an object named “myData.” This object is of a type called a data frame in R. It has the same row and column format as did the .csv file. The data in the data frame can be viewed in the console by typing the name of the data frame and pressing return.

The read.csv command above included two optional arguments: “strip.white = TRUE” omits white space at the beginnings and ends of character data cells; “header = TRUE” indicates that the first row in the data file is a list of column (variable) names. If the data file does not have variable names in the first row, then either set this to FALSE or simply omit the argument. Note that an error message “incomplete final line found by readTableHeader” is sometimes generated with the read.csv command because Microsoft Excel and some other programs do not put end-of-line markers on the last lines of .csv or .txt files. This message can be ignored.

It is best not to put quotes around column names or character entries in the data file. If the data file comes with quotes, use a text editor to search for and remove them. Missing data can be indicated by a special symbol, or better, by simply having white space or nothing between commas in the position of the empty cell.

Example data

The data file that is used to illustrate bootES in this article, “example.csv,” is provided automatically with the bootES package, and can be imported using the following command:

Exporting data

The R command for exporting data frames is write.table(), but we recommend the convenience version write.csv(), which writes comma-separated value files. This command takes as arguments the name of the data frame (e.g., myData) and the name of the new data file (e.g., file = “myNewData.csv”). To avoid storing default row numbers as row names in the data file include the argument “row.names = FALSE.” The complete command is

This will save the data file in the default directory on your hard disk.

Saving commands and results

The entire R session in the console can be saved to a text file by choosing “Save as…” from the File menu. This has the advantage of saving results along with the commands that generated them. Individual results may be copied from this file, or directly from the R console, and pasted into other programs.

Selecting variables (columns)

Data frames often contain multiple columns. There are many ways to select subsets of columns in R, and here we describe the one that we believe is the most transparent to new users. Named columns within a data frame can be specified by attaching the column name as a suffix to the name of the data frame, following a $ sign, as in dataFrame$columnName. For example, if we wish to pick out the column “Meas1” from the data frame “myData,” the proper designation would be “myData$Meas1.” This usage was illustrated above when we found the mean and CI for a single variable.

Note that in bootES, some analyses require that one specify a data column and, in some instances, a grouping column. In those analyses, the name of the data frame is given as the first argument to bootES and must be omitted from the column names. So we use

and not

Finally, some analyses in R and bootES require that we pick out multiple columns at once from our data frame. An easy way to accomplish this is to concatenate the variable names using R’s concatenation function, c(), and then wrap this in square brackets following the data frame name. For example, if we wanted to pick out both columns “Meas1” and “Meas2” from the data frame myData, the command would look like this:

This notation was used above to pick out columns in the correlation examples.

Selecting data subsets (rows)

Sometimes one might want to perform an analysis on a subset of rows (subjects or cases), such as some particular group. To pick out subsets of rows from a data frame, a transparent approach is to use R’s subset() command. For example, to select only those rows in myData corresponding to female subjects in condition A, we can use the command

This creates a new data frame, which we arbitrarily named “female.A,” containing only those cases. (Note that the dot, or period, in a name in R, as in “female.A,” is used merely as a means of clarifying the label; in this context, it is not an operation.) Any analyses on the data frame female.A will return results only for that group of subjects.

In the subset() function, multiple necessary conditions are combined with an ampersand (denoting and), whereas alternative sufficient conditions are combined using a vertical bar “|” (denoting or). Equality is denoted with a double equal sign (==), and “not equal” is denoted “!=”. Inequalities are denoted with their usual symbols (>, <, >=, and < =).

Appendix 2

Bias-corrected-and-accelerated (BCa) intervals

As was noted above, simple “percentile” bootstrap CIs suffer from two sources of inaccuracy. First, many sample statistics are biased estimators of their corresponding population parameters, such that the expected value of $\widehat{\theta}$ does not equal θ. We can estimate bias using the distribution of the statistic from our bootstrap resamples (Efron, 1987; Efron & Tibshirani, 1993). Find the proportion, p, of the ${{\widehat{\theta}}^{*}}$s that are less than $\widehat{\theta}:p=count\left( {{{\widehat{\theta}}^{*}} < \widehat{\theta}} \right)/R$, where R is the number of resamples. Then find the value, z, that is greater than 100p% of the normal distribution; that is, find the inverse of a standard normal cumulative distribution function (NCDF ⁻¹) for quantile p:

$$ z=NCD{F^{-1 }}(p). $$

(8)

Thus, z measures the discrepancy between $\widehat{\theta}$ and the median of the distribution of ${{\widehat{\theta}}^{*}}$ and serves as a measure of median bias (Efron & Tibshirani, 1993, p. 186). When $\widehat{\theta}$ is equal to the median of the ${{\widehat{\theta}}^{*}}$, then z equals 0, indicating no bias. If $\hat{\theta}$ were, say, greater than only 40 % of the ${{\widehat{\theta}}^{*}}$, then z would be approximately −0.25, indicating a negative bias.

The second source of inaccuracy in percentile bootstrap CIs is that the standard error of an estimate of $\widehat{\theta}$ may not be independent of the value of θ. We can estimate this dependency from the rate of change, called the acceleration, of $\widehat{\theta}$ with respect to change in θ. Acceleration, a, may be estimated from the distribution of jackknife values of the statistic. To find a jackknife value, we omit one data point from the original sample and recompute the statistic. Let X _–i be the data omitting the ith data point; then, ${{\widehat{\theta}}_{-i }}$ is the statistic of interest calculated for the remaining N − 1 data points. We repeat this for each data point in the original data, giving us N different values of ${{\widehat{\theta}}_{-i }}$. Denote the mean of the N jackknife values $\overline{\theta}$. The acceleration can now be calculated from the following equation (Efron & Tibshirani, 1993, p. 186):

$$ a=\frac{{\sum {\left( {\overline{\theta}-{{\widehat{\theta}}_{-i }}} \right)} }}{{6{{{\left[ {\sum {{{{\left( {\overline{\theta}-{{\widehat{\theta}}_{-i }}} \right)}}^2}} } \right]}}^{{{3 \left/ {2} \right.}}}}}}. $$

(9)

The bias in $\widehat{\theta}$, as estimated in Eq. 8, and the dependency between the standard error and θ, as estimated in Eq. 9, can now be used to adjust the percentile cutoffs in the distribution of ${{\widehat{\theta}}^{*}}$ to create more accurate bootstrap CIs than those from unadjusted percentiles. Keeping with standard notation in psychology, for a CI with a P% confidence level, let α = 1 – P/100. That is, α is the combined proportions of the lower and upper tails of the distribution that are not covered by the CI. For example, for a 95 % CI, P is 95, so α is 0.05. (In contrast, Efron & Tibshirani, 1993, defined α as the area in a single tail of the distribution, such that 2α = 1 − P/100.) Let Z(α/2) be the value on a standard normal distribution that cuts off 100α/2 % of the lower tail of the distribution. For example, for α = 0.05, Z(.025) = −1.96.

In Efron’s (1987) procedure for finding the BCa percentiles, we adjust these Z values by adding to them the bias estimate, z, and dividing by a term that contains the acceleration estimate, a. This gives a new value on a standard normal distribution that can be converted back into a percentile using the NCDF. The lower percentile, q _low , is found from

$$ {q_{low }}=NCDF\left\{ {z+\frac{{z+Z\left( {{\alpha \left/ {2} \right.}} \right)}}{{1+a\left[ {z+Z\left( {{\alpha \left/ {2} \right.}} \right)} \right]}}} \right\}. $$

(10)

Likewise, Z(1 − α/2) is the value on a standard normal distribution that cuts off 100α/2 % of the upper tail of the distribution. For example, for α = 0.05, Z(.975) = 1.96. Thus, the upper percentile, q _hi , is found from

$$ {q_{ki }}=NCDF\left\{ {z+\frac{{z+Z\left( {1-{\alpha \left/ {2} \right.}} \right)}}{{1+a\left[ {z+Z\left( {1-{\alpha \left/ {2} \right.}} \right)} \right]}}} \right\}. $$

(11)

Finally, these percentiles, q _low and q _hi , are used to pick out the corresponding values of ${{\widehat{\theta}}^{*}}$ in the rank ordered resampled values of the statistic. Note that when bias is zero (z = 0) and the standard error is constant (a = 0), q _low = α/2 and q _hi  = 1 − α/2, so these formulas yield the same values as the simple percentile method.