Abstract
Research on temporal-order perception uses temporal-order judgment (TOJ) tasks or synchrony judgment (SJ) tasks in their binary SJ2 or ternary SJ3 variants. In all cases, two stimuli are presented with some temporal delay, and observers judge the order of presentation. Arbitrary psychometric functions are typically fitted to obtain performance measures such as sensitivity or the point of subjective simultaneity, but the parameters of these functions are uninterpretable. We describe routines in MATLAB and R that fit model-based functions whose parameters are interpretable in terms of the processes underlying temporal-order and simultaneity judgments and responses. These functions arise from an independent-channels model assuming arrival latencies with exponential distributions and a trichotomous decision space. Different routines fit data separately for SJ2, SJ3, and TOJ tasks, jointly for any two tasks, or also jointly for the three tasks (for common cases in which two or even the three tasks were used with the same stimuli and participants). Additional routines provide bootstrap p-values and confidence intervals for estimated parameters. A further routine is included that obtains performance measures from the fitted functions. An R package for Windows and source code of the MATLAB and R routines are available as Supplementary Files.
Similar content being viewed by others
Research on the perception of temporal order uses simultaneity judgment (SJ) tasks or temporal-order judgment (TOJ) tasks. In either case, each trial in a series presents two stimuli with some temporal delay (or stimulus onset asynchrony; SOA). The stimuli may belong to different sensory modalities, and one of them is experimentally defined as the reference, whereas the other is regarded as the test whose delay with respect to the reference is manipulated. Across trials, the onset of the test stimulus may occur from well before the onset of the reference (yielding delays or SOAs that are defined as negative by convention) to well after it (yielding positive delays). The response requested from the observer varies with the task. In the binary SJ2 version of SJ tasks, observers are asked to judge whether stimuli were presented simultaneously (yielding S responses) or asynchronously (yielding A responses); in the ternary SJ3 variant, observers are instead asked to judge whether the reference was presented first (yielding RF responses), the test was presented first (yielding TF responses), or presentation was simultaneous (yielding S responses). In TOJ tasks, observers must simply report whether they judged that the test stimulus was presented before or after the reference, only allowing TF or RF responses and forcing observers to guess when they judge that presentation was simultaneous. Psychometric functions are then fitted to the proportion of responses of each type as a function of delay. Performance measures (e.g., the point of subjective simultaneity; PSS) are also extracted from the fitted functions.
Often, the fitted psychometric functions (usually Gaussian or logistic functions) have the only purpose of describing the path of the data sufficiently accurately to obtain dependable estimates of these performance measures. This strategy seems adequate to establish, for instance, that SJ and TOJ tasks yield significantly different estimates of the PSS, because the fitted curves describe sufficiently adequately the skeleton of the data even if the fit is not good according to some statistic or if the model underlying the fitted psychometric function is not adequate. However, this strategy cannot indicate the cause of these differences, because the parameters of the fitted functions are not linked to the processes presumably governing performance. The functions, then, are mere descriptions of the data and do not permit testing hypotheses about differences in these underlying processes across tasks or across experimental conditions (e.g., in studies of prior entry): Only observed performance is captured in the estimated parameters, but at the cost of an excessively large number of parameters (as many as 24; see García-Pérez & Alcalá-Quintana, 2012a) and with the questionable outcome that the psychometric functions fitted to SJ3 data do not add up to unity.
There is a second reason why fitting arbitrary Gaussian or logistic functions to SJ and TOJ data is not advisable. These functions are symmetric and smooth, whereas the path described by empirical proportions of S responses in SJ tasks is well-known to be generally asymmetric for each individual observer and the path described by RF responses in TOJ tasks often shows a more or less pronounced plateau midway along the range of SOAs for each individual observer. Although these asymmetries and irregularities average out if data from all observers are aggregated, Gaussian or logistic functions fitted to each observer’s data cannot accommodate these characteristics and, then, are inadequate, despite their acceptable description of the rough skeleton of the data.
An alternative approach consists of adopting a generative model that describes the processes underlying judgments and responses in SJ and TOJ tasks, producing psychometric functions that also allow obtaining conventional performance measures but whose parameters capture the underlying processes. Random-walk models (e.g., Heath, 1984) or diffusion models (e.g., Schwarz, 2006) have been proposed to account for performance in TOJ tasks, but these models do not seem to have ever been extended for application to SJ2 or SJ3 tasks (and how to do this is anything but trivial). In contrast, independent-channels models are suitable candidates because they can readily be tailored to SJ2, SJ3, or TOJ tasks and they additionally give rise to psychometric functions that describe the empirical asymmetries and irregularities of S and RF data discussed in the preceding paragraph. Recourse to the alternative strategy based on independent-channels models has shown that errors in the process by which unobservable judgments turn into observed responses account for some empirical characteristics of SJ data that had been regarded as evidence against these models (García-Pérez & Alcalá-Quintana, 2012b) and it has also shown that the discrepancies between performance measures in SJ and TOJ tasks reflect differences in the decisional aspects that determine judgments (García-Pérez & Alcalá-Quintana, 2012a). Unpublished results show that psychometric functions arising from these models also describe adequately the asymmetries and irregularities of the data from individual observers in the experiments reported by Schneider and Bavelier (2003), Keetels and Vroomen (2008), Fujisaki and Nishida (2009), Vroomen and Stekelenburg (2011), and Yates and Nicholls (2011), as well as in data from other yet unpublished studies. In contrast, the fit of conventional logistic or Gaussian functions to these data is generally much poorer, particularly for SJ2 data.
Fitting independent-channels models is more complex than fitting Gaussian or logistic functions to data, and this article presents routines that attain this goal in two popular programming environments: MATLAB (http://www.mathworks.com) and R (http://cran.r-project.org). The model that these routines fit is described in the next section, and the remainder of the article documents and illustrates the routines. Different routines fit the model to SJ2, SJ3, and TOJ data either separately (when data were collected with a single task) or jointly (when data were collected from the same participants and stimuli with any two tasks or with the three of them). Additional routines provide bootstrap confidence intervals and p-values for the estimated parameters. A further routine computes performance measures from the fitted functions. A comparative analysis of the routines across environments is also reported, and usage recommendations are given.
Model of simultaneity and temporal-order judgments
A thorough description of the model is given in García-Pérez and Alcalá-Quintana (2012a, 2012b), but a brief account is given next. The model is a version of the independent-channels model 3 of Sternberg and Knoll (1973) and assumes that the arrival latencies T t and T r of test and reference stimuli are random variables with shifted exponential distributions:
where Δt i (in milliseconds) is the onset of the corresponding stimulus, λ i is the rate parameter (in milliseconds−1), and τ i (in milliseconds) is a processing delay. Exponential distributions embody the crucial property that the time at which sensory signals reach a central mechanism cannot precede the onset of the stimulus triggering that signal. These distributions are thus commonly used to describe arrival latencies or peripheral processing times (see, e.g., Colonius & Diederich, 2011; Diederich & Colonius, 2011; Heath, 1984). Furthermore, the parameters of shifted exponential distributions are readily interpretable: The mean of a variable distributed as in Equation 1 is 1/λ i + τ i , and the standard deviation is 1/λ i . Thus, parameters λ i and τ i describe positive-valued arrival latencies whose mean and standard deviation may vary independently. The origin of time is set at the onset of the reference stimulus so that Δt r = 0 and Δt ≡ Δt t is the delay (or SOA) that is manipulated. Thus, Δt < 0 (Δt > 0) reflects that the test stimulus preceded (followed) the reference stimulus. The observer’s judgment arises from a decision rule applied to the arrival-time difference D = T t − T r, that has the bilateral exponential distribution
where τ = τt − τr. A resolution parameter δ (in milliseconds) limits the observer’s ability to resolve small differences in arrival latency so that a TF judgment occurs when D is sufficiently large and negative (i.e., D < −δ), an RF judgment occurs when D is sufficiently large and positive (D > δ), and an S judgment arises when the arrival-time difference does not exceed the resolution limit (−δ ≤ D ≤ δ). Thus, the probabilities of TF, S, and RF judgments as a function of Δt are
where
Judgments are not always reliably reported, either as a result of errors in pressing the response keys or because of factors that affect the judgments themselves (e.g., lapses of attention, blinks when visual stimuli are involved, etc.). The latter can be reasonably left out without consequences (see García-Pérez & Alcalá-Quintana, 2012b) but consideration of response errors is crucial. Thus, let εTF, εS, and εRF be the probabilities that the observer misreports TF, S, and RF judgments, respectively, as a result of a response error. Misreporting a given judgment can take two forms, since there are two other alternative judgments. Let κX-Y be the bias toward misreporting an X judgment as a Y judgment so that κX-Z = 1 − κX-Y is the bias toward misreporting an X judgment as a Z judgment. Only three bias parameters are free—say, κTF-S, κS-TF, and κRF-TF, because \( {\kappa_{{\mathrm{TF}-\mathrm{RF}}}}=1-{\kappa_{{\mathrm{TF}-\mathrm{S}}}},\ {\kappa_{{\mathrm{S}-\mathrm{RF}}}}=1 - {\kappa_{{\mathrm{S}-\mathrm{TF}}}} \), and \( {\kappa_{{\mathrm{RF}-\mathrm{S}}}}=1-{\kappa_{{\mathrm{RF}-\mathrm{TF}}}} \). For SJ3 tasks, where the three judgments and responses are involved, the model expressing probabilities of observed responses (whether faithful reports or misreports) is
In SJ2 tasks, where RF and TF judgments both map onto A judgments, the model expressing probabilities of observed responses is
Finally, in TOJ tasks, where S responses are not allowed, observers must give TF or RF responses for S judgments. This is done at random, possibly with some response bias (see Sternberg & Knoll, 1973; Schneider & Bavelier, 2003), so let ξ be the probability that the observer gives an RF response for an S judgment. Then, the model expressing probabilities of observed responses in TOJ tasks is
The model for each task thus includes three parameters (λ r, λ t, and τ) describing aspects of the arrival latencies underlying the perception of temporal order and a further parameter (δ) describing the ability of the observer at resolving small differences in arrival latency. The model for TOJ tasks includes a further response bias parameter (ξ) that is unique to this task. And the model for each task includes additional parameters for response errors: three in the SJ2 task (εSJ2-TF, εSJ2-S, and εSJ2-RF), six in the SJ3 task (εSJ3-TF, εSJ3-S, εSJ3-RF, κS-TF, κRF-TF, and κTF-S), and two in the TOJ task (εTOJ-TF and εTOJ-RF).
Empirical data show that errors do not always occur in all forms under all tasks and for all observers (García-Pérez & Alcalá-Quintana, 2012a, 2012b), which requires consideration of the full set of models arising for each task by removal of all possible subsets of response error parameters. As can be seen in Table 1, this yields eight variants for the SJ2 task (one case in which all the ε parameters are removed, one case in which all of them are included, three cases in which only one of the ε parameters is removed, and three more cases in which two of them are removed), another eight variants for the SJ3 task (identical to those just described, because removal of an ε parameter also removes its accompanying κ parameter), and four variants for the TOJ task (one case in which the two ε parameters are removed, another case in which they are both included, and two cases in which only one of them is removed). For all tasks, error model 0 is the simplest version, assuming that response errors do not occur. This assumption renders a model with the least number of free parameters: only four (λr, λt, τ, and δ) in SJ2 and SJ3 tasks and five (the previous four plus ξ) in TOJ tasks. Error model 1 is for all tasks the full model described above and renders the largest number of free parameters per task (seven in SJ2 and TOJ tasks and ten in SJ3 tasks, as discussed above). The remaining models for each task represent intermediate cases (in terms of number of free error parameters) and exhaust all the possibilities for each particular task. The routines to be described below are designed so that users can choose between fitting a particular version of the model for the applicable task(s) or requesting that the full set of models be considered and parameter estimates returned for the model that best fits the data according to the Bayesian information criterion (BIC).
 ) or excluded (
) or excluded ( ) across models for response errors in each task
) across models for response errors in each taskDescription of the routines
Psychometric functions are fitted to counts of responses at each of a number of delays. Figure 1 gives artificial data from SJ2, SJ3, and TOJ tasks that will be used in the examples to follow. A given experimental condition may use only one of these tasks (see, e.g., Yates & Nicholls, 2011; Zampini, Guest, Shore, & Spence, 2005; Zampini, Shore, & Spence, 2003), or it may use two or more of them with the same stimuli and participants (see, e.g., Fujisaki & Nishida, 2009; Schneider & Bavelier, 2003; van Eijk, Kohlrausch, Juola, & van de Par, 2008, 2010). For this reason, separate routines have been written that fit the model separately to data from each individual task, jointly to data from pairs of tasks, and also jointly to data from the three tasks. In the two latter cases, the joint fit implies that parameters describing the distribution of arrival latencies (λ r, λ t, and τ) are regarded as common to all tasks because these distributions must be identical if stimuli and attentional conditions do not change across tasks (for empirical evidence to this effect, see García-Pérez & Alcalá-Quintana, 2012a). Thus, these parameters are forced to take on the same values across tasks, whereas the remaining parameters are separately estimated for each task.Footnote 1
Artificial SJ2, SJ3, and TOJ data. Note that the number of delay levels varies across tasks and that the number of trials per level also varies within and across tasks. The routines described here can handle all these cases even when the model is fitted jointly to data from the three tasks. The spacing of delay levels is fixed in this example (at 60 ms for SJ2 data and at 50 ms for SJ3 and TOJ data), but this need not be so either
Maximum-likelihood parameter estimates are sought with the MATLAB function  or the R function
or the R function  , in both cases using a quasi-Newton algorithm.Footnote 2 The routines impose user-defined bounds on estimates of λ
r and λ
t (to be discussed below). Theoretically, λ
r and λ
t are bounded only to be positive, but we found out that narrowing their range down to realistic limits renders more stable and faster performance and, according to our simulation studies, this bounding does not reduce the accuracy with which true parameters can be estimated. Analogously, parameter δ is constrained only to be positive under the model, and parameter τ is constrained only to be real, but the routines also allow users to bound the ranges for these parameters if desired. Error and bias parameters are always bounded in the interval [0, 1] without user intervention.
, in both cases using a quasi-Newton algorithm.Footnote 2 The routines impose user-defined bounds on estimates of λ
r and λ
t (to be discussed below). Theoretically, λ
r and λ
t are bounded only to be positive, but we found out that narrowing their range down to realistic limits renders more stable and faster performance and, according to our simulation studies, this bounding does not reduce the accuracy with which true parameters can be estimated. Analogously, parameter δ is constrained only to be positive under the model, and parameter τ is constrained only to be real, but the routines also allow users to bound the ranges for these parameters if desired. Error and bias parameters are always bounded in the interval [0, 1] without user intervention.
The  and
and  functions must be initialized by providing starting values for each parameter, and they are not guaranteed to return the global optimum. These starting values must be provided by the user, and our routines accept multiple starting values for each parameter (examples are given and discussed below). The routines then factorially combine the sets of starting values for each parameter and obtain a solution for each multidimensional starting point, returning the optimal solution across the board. We will first describe and illustrate the routine that fits psychometric functions jointly to data from the three tasks, which greatly simplifies the description of the other routines.
functions must be initialized by providing starting values for each parameter, and they are not guaranteed to return the global optimum. These starting values must be provided by the user, and our routines accept multiple starting values for each parameter (examples are given and discussed below). The routines then factorially combine the sets of starting values for each parameter and obtain a solution for each multidimensional starting point, returning the optimal solution across the board. We will first describe and illustrate the routine that fits psychometric functions jointly to data from the three tasks, which greatly simplifies the description of the other routines.
Fitting psychometric functions jointly to data from the three tasks
The calling statements of the MATLAB and R routines are, respectively,

and

In either case, input arguments are as follows:
-
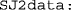 3 × N
SJ2 matrix with data from the SJ2 task arranged as in Fig. 1; that is, the first row gives the N
SJ2 delays at which data were collected, the second row gives the count of A responses at each delay, and the third row gives the count of S responses at each delay.
3 × N
SJ2 matrix with data from the SJ2 task arranged as in Fig. 1; that is, the first row gives the N
SJ2 delays at which data were collected, the second row gives the count of A responses at each delay, and the third row gives the count of S responses at each delay. -
 4 × N
SJ3 matrix with data from the SJ3 task arranged as in Fig. 1; that is, the first row gives the N
SJ3 delays at which data were collected, the second row gives the counts of TF responses, the third row gives the counts of S responses, and the fourth row gives the counts of RF responses.
4 × N
SJ3 matrix with data from the SJ3 task arranged as in Fig. 1; that is, the first row gives the N
SJ3 delays at which data were collected, the second row gives the counts of TF responses, the third row gives the counts of S responses, and the fourth row gives the counts of RF responses. -
 3 × N
TOJ matrix with data from the TOJ task arranged as in Fig. 1; that is, the first row gives the N
TOJ delays at which data were collected, the second row gives the counts of TF responses, and the third row gives the counts of RF responses.
3 × N
TOJ matrix with data from the TOJ task arranged as in Fig. 1; that is, the first row gives the N
TOJ delays at which data were collected, the second row gives the counts of TF responses, and the third row gives the counts of RF responses. -
 A 1 × 2 row vector stating the lower and upper bounds for both λr and λt (positive reals).
A 1 × 2 row vector stating the lower and upper bounds for both λr and λt (positive reals). -
 A 1 × 2 row vector stating the lower and upper bounds for τ (reals). The suggested option for general use is
A 1 × 2 row vector stating the lower and upper bounds for τ (reals). The suggested option for general use is 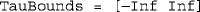 , to be changed only in a re-rerun with the same data to prevent untenably large estimates (in absolute value) that will, nevertheless, rarely be obtained even when the data are scarce.
, to be changed only in a re-rerun with the same data to prevent untenably large estimates (in absolute value) that will, nevertheless, rarely be obtained even when the data are scarce. -
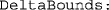 A 1 × 2 row vector stating the lower and upper bounds for δ (positive reals). The suggested option for general use is
A 1 × 2 row vector stating the lower and upper bounds for δ (positive reals). The suggested option for general use is 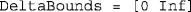 , to be changed only in a re-rerun with the same data to prevent untenably large estimates that will, nevertheless, rarely be obtained even when the data are scarce.
, to be changed only in a re-rerun with the same data to prevent untenably large estimates that will, nevertheless, rarely be obtained even when the data are scarce. -
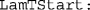 Starting value(s) for parameter λt. This argument must be a positive real and can be a scalar (to set a single starting value) or a row vector (to set several of them).
Starting value(s) for parameter λt. This argument must be a positive real and can be a scalar (to set a single starting value) or a row vector (to set several of them). -
 Starting value(s) for parameter λr (positive real). Can be a scalar or a row vector.
Starting value(s) for parameter λr (positive real). Can be a scalar or a row vector. -
 Starting value(s) for parameter τ (real). Can be a scalar or a row vector.
Starting value(s) for parameter τ (real). Can be a scalar or a row vector. -
 Starting value(s) for parameter δ (positive real). Can be a scalar or a row vector.
Starting value(s) for parameter δ (positive real). Can be a scalar or a row vector. -
 Starting value(s) for all response error parameters (εTF, εS, and εRF for each task), in the interval [0, 1]. Can be a scalar or a row vector.
Starting value(s) for all response error parameters (εTF, εS, and εRF for each task), in the interval [0, 1]. Can be a scalar or a row vector. -
 Starting value(s) for parameter ξ and for all κs, in the interval [0, 1]. Can be a scalar or a row vector.
Starting value(s) for parameter ξ and for all κs, in the interval [0, 1]. Can be a scalar or a row vector. -
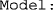 Choice of model, according to codes given in Table 1. For the choice of an individual version of the model for each task, this argument must be a 1 × 3 row vector whose first, second, and third components are, respectively, the chosen models for the SJ2 task (an integer scalar between 0 and 7, inclusive), the SJ3 task (also an integer scalar between 0 and 7, inclusive), and the TOJ task (an integer scalar between 0 and 3, inclusive). Because models 0 and 1 are analogous for all tasks (see Table 1), the cases
Choice of model, according to codes given in Table 1. For the choice of an individual version of the model for each task, this argument must be a 1 × 3 row vector whose first, second, and third components are, respectively, the chosen models for the SJ2 task (an integer scalar between 0 and 7, inclusive), the SJ3 task (also an integer scalar between 0 and 7, inclusive), and the TOJ task (an integer scalar between 0 and 3, inclusive). Because models 0 and 1 are analogous for all tasks (see Table 1), the cases 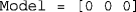 and
and 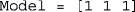 —or, in R,
—or, in R,  and
and 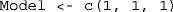 — can be simplified to a single scalar (i.e.,
— can be simplified to a single scalar (i.e., 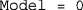 or
or 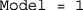 ). For the routine to return the best-fitting model by the BIC, set
). For the routine to return the best-fitting model by the BIC, set 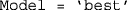 (case insensitive).
(case insensitive). -
 A logical scalar. If true, a plot showing data and fitted functions is created; otherwise, no plot is created.
A logical scalar. If true, a plot showing data and fitted functions is created; otherwise, no plot is created. -
 A logical scalar. If true, messages are issued to the console as the routine progresses. If a single model was selected, a message is issued for each of the multidimensional starting points used (see an example in the Final Comments section); if
A logical scalar. If true, messages are issued to the console as the routine progresses. If a single model was selected, a message is issued for each of the multidimensional starting points used (see an example in the Final Comments section); if 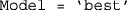 , a message is issued for each candidate model, omitting messages for each of the multidimensional starting points used. Setting true this argument also issues a message if the estimates of λr or λt lie at one of the bounds defined in
, a message is issued for each candidate model, omitting messages for each of the multidimensional starting points used. Setting true this argument also issues a message if the estimates of λr or λt lie at one of the bounds defined in  .
.
The output returned in  is a structure (in MATLAB; it is a list in R) including parameter estimates and complete information about the outcome of the routine (to be described after the following example). For the data in Fig. 1, the MATLAB script
is a structure (in MATLAB; it is a list in R) including parameter estimates and complete information about the outcome of the routine (to be described after the following example). For the data in Fig. 1, the MATLAB script

produces the plot shown in Fig. 2 and the  structure shown in Fig. 3. Note that the assignment
structure shown in Fig. 3. Note that the assignment  is equivalent to
is equivalent to  , as discussed above. Note also that the lower and upper bounds for λ
r and λ
t are defined as 1/200 and 1/3, respectively. Recall that 1/λ
i
represents the standard deviation of the distribution of arrival latencies (in milliseconds) so that these bounds implicitly restrict the search to distributions whose standard deviation ranges from 3 to 200 ms. It is unlikely that the actual standard deviations will be outside this range. If the lower bound of the input range turned out to be too high for a given data set, this would show in that final estimates of λr or λt lie at this bound and it is thus easy to lower this bound and rerun (a message to this effect is issued to the console when
, as discussed above. Note also that the lower and upper bounds for λ
r and λ
t are defined as 1/200 and 1/3, respectively. Recall that 1/λ
i
represents the standard deviation of the distribution of arrival latencies (in milliseconds) so that these bounds implicitly restrict the search to distributions whose standard deviation ranges from 3 to 200 ms. It is unlikely that the actual standard deviations will be outside this range. If the lower bound of the input range turned out to be too high for a given data set, this would show in that final estimates of λr or λt lie at this bound and it is thus easy to lower this bound and rerun (a message to this effect is issued to the console when  ). Final estimates of λr or λt at the upper bound of the range reflect a characteristic that is discussed in detail in Appendix 3 of García-Pérez and Alcalá-Quintana (2012a), which essentially reveals uninformative data for the estimation of that particular parameter (a message to this effect is also be issued to the console when
). Final estimates of λr or λt at the upper bound of the range reflect a characteristic that is discussed in detail in Appendix 3 of García-Pérez and Alcalá-Quintana (2012a), which essentially reveals uninformative data for the estimation of that particular parameter (a message to this effect is also be issued to the console when  ). Readers are referred to the appendix just mentioned for a thorough treatment of this issue but we should stress also that the remaining parameter estimates are still meaningful in these conditions and that a rerun with a higher upper bound is not sensible: The current upper bound at 1/3 already implies that the standard deviation of arrival latencies is 3 ms, a seemingly implausibly low value. If anything, what should be done in these cases is to reduce the upper bound before rerunning, but a thorough discussion of this issue is deferred to the Final Comments section.
). Readers are referred to the appendix just mentioned for a thorough treatment of this issue but we should stress also that the remaining parameter estimates are still meaningful in these conditions and that a rerun with a higher upper bound is not sensible: The current upper bound at 1/3 already implies that the standard deviation of arrival latencies is 3 ms, a seemingly implausibly low value. If anything, what should be done in these cases is to reduce the upper bound before rerunning, but a thorough discussion of this issue is deferred to the Final Comments section.
Output from the routine that fits the model jointly to data from the three tasks. The dash–dot line near the bottom indicates expected frequencies of 5, so that model lines below this limit at locations where data exist represent cells that may threaten the validity of goodness-of-fit statistics. The dotted line (barely visible just above the horizontal axis) similarly indicates expected frequencies of 1
Output structure accompanying the plot in Fig. 2. Note that expected frequencies are lower than 5 in 23 out of 91 cells and 19 of those cells have nonnull observed frequencies. Analogous counts for cells with expected frequencies below 1 are 6 and 2
The output structure (see Fig. 3) includes a label for the problem (field 1) and output from  (fields 2–4),Footnote 3 the error model selected by the user and the model for which parameters are returned (fields 5 and 6),Footnote 4 the number of free parameters in the fitted model (field 7), the overall number of cells for the goodness-of-fit tests, the number of cells in which expected frequencies were smaller than 5 and the number of those cells in which observed frequencies were nonnull (fields 8–10), the number of cells in which expected frequencies were smaller than 1 and the number of those cells in which observed frequencies were nonnull (fields 11 and 12),Footnote 5 the degrees of freedom, values, and asymptotic p-values of the chi-square (X
2) and likelihood-ratio (G
2) goodness-of-fit statistics (fields 13–17), the BIC of the fitted model (field 18), the user-defined bounds in
(fields 2–4),Footnote 3 the error model selected by the user and the model for which parameters are returned (fields 5 and 6),Footnote 4 the number of free parameters in the fitted model (field 7), the overall number of cells for the goodness-of-fit tests, the number of cells in which expected frequencies were smaller than 5 and the number of those cells in which observed frequencies were nonnull (fields 8–10), the number of cells in which expected frequencies were smaller than 1 and the number of those cells in which observed frequencies were nonnull (fields 11 and 12),Footnote 5 the degrees of freedom, values, and asymptotic p-values of the chi-square (X
2) and likelihood-ratio (G
2) goodness-of-fit statistics (fields 13–17), the BIC of the fitted model (field 18), the user-defined bounds in  , and
, and  (fields 19–21), and estimated values for the 21 model parameters (fields 22–42; as discussed above, some of the κs are not free parameters, and error and bias parameters not included in the fitted model are returned as NaN in MATLAB and as NA in R).Footnote 6 The output list from the R routine differs only as to fields 2 and 3, which instead give output diagnostic information from
(fields 19–21), and estimated values for the 21 model parameters (fields 22–42; as discussed above, some of the κs are not free parameters, and error and bias parameters not included in the fitted model are returned as NaN in MATLAB and as NA in R).Footnote 6 The output list from the R routine differs only as to fields 2 and 3, which instead give output diagnostic information from  : convergence code (field 2) and text message accompanying the convergence code, if any (field 3).
: convergence code (field 2) and text message accompanying the convergence code, if any (field 3).
Figure 2 also reveals that our artificial data reflect one of the patterns of response errors shown by empirical data (see García-Pérez & Alcalá-Quintana, 2012a, 2012b). The left panel of Fig. 2 shows an almost null proportion of S responses at long negative delays in the SJ2 task (as would be expected) but shows a nonnull proportion of S responses at long positive delays, as if some RF judgments had been misreported as S responses. SJ3 data in the center panel are consistent with response errors of this type: At long negative delays, TF responses do not reach 100%, and some TF judgments seem to be misreported as RF responses (something that would not show in SJ2 data because TF and RF judgments or misreports end up as A responses); in contrast, at long positive delays, RF responses do not reach 100%, and some of the RF judgments seem to be misreported as S responses, just as was the case in the SJ2 task.
In this example, we chose to fit the full model including all error parameters for illustration. A rerun using  rendered
rendered  as the fitted model, whose BIC was 3,281.9 (as compared with 3,295.7 in the preceding run, as seen in Fig. 3),Footnote 7 with no meaningful change in the estimates of the sensory parameters λ
t, λ
r, and τ or the decisional parameters δ. This outcome is easily understood: Given the near-zero estimated values for most error parameters ε when
as the fitted model, whose BIC was 3,281.9 (as compared with 3,295.7 in the preceding run, as seen in Fig. 3),Footnote 7 with no meaningful change in the estimates of the sensory parameters λ
t, λ
r, and τ or the decisional parameters δ. This outcome is easily understood: Given the near-zero estimated values for most error parameters ε when  (see Fig. 3), a rerun with
(see Fig. 3), a rerun with  determines that a more parsimonious account of the data can be given by fixing some of these error parameters to zero, as implied in model 5 for the SJ2 and SJ3 tasks and in model 2 for the TOJ task (see Table 1).
determines that a more parsimonious account of the data can be given by fixing some of these error parameters to zero, as implied in model 5 for the SJ2 and SJ3 tasks and in model 2 for the TOJ task (see Table 1).
For illustration, the R script for the previous example is

Note that using the R routines under Windows requires loading the package  at the beginning of the session. This package must also have been installed as any other R package.
at the beginning of the session. This package must also have been installed as any other R package.
Fitting psychometric functions in other cases
The calling statements for the routines that fit psychometric functions jointly to data from pairs of tasks are straightforward modifications of the preceding one. Only the MATLAB calling statements are given, since those for R are analogous modifications:

Note that this has a straightforward implication on the user’s specification of the argument  . The simplified scalar options 0 or 1 and the string option
. The simplified scalar options 0 or 1 and the string option  are still valid, but the general form of the single-version option now requires a 1 × 2 row vector with components within the applicable range for the implied models: 0–7 and 0–7 in the case of
are still valid, but the general form of the single-version option now requires a 1 × 2 row vector with components within the applicable range for the implied models: 0–7 and 0–7 in the case of  , 0–7 and 0–3 for
, 0–7 and 0–3 for  , and also 0–7 and 0–3 for
, and also 0–7 and 0–3 for  .
.
To fit psychometric functions to data from a single task, the MATLAB calling statements are

and note that  is the only routine whose calling statement does not include
is the only routine whose calling statement does not include  , because its reference parameters (ξ and all κs) are not involved in SJ2 tasks. Again, this has a straightforward implication on the user’s specification of the argument
, because its reference parameters (ξ and all κs) are not involved in SJ2 tasks. Again, this has a straightforward implication on the user’s specification of the argument  . The string option
. The string option  is still valid, but the single-version options now reduce to a scalar in the applicable range for the implied task: 0–7 for
is still valid, but the single-version options now reduce to a scalar in the applicable range for the implied task: 0–7 for  and
and  and 0–3 for
and 0–3 for  .
.
As a further example involving the data in Fig. 1, fitting the model separately for each task through the MATLAB script

produces the plots in Fig. 4 and output structures that vary according to the task for which the model was fitted. All output structures have the general form in Fig. 3, but they include only the applicable parameters for the task(s), as illustrated in Fig. 5 for  in the preceding example.
in the preceding example.
Output structure accompanying the plot for SJ2 data in Fig. 4. Fields 1–21 have similar content in all output structures, and it is only the remaining fields that vary across tasks according to the number of parameters in the model
Bootstrap confidence intervals and p-values
The fitting routines just described return point estimates for model parameters and asymptotic p-values from the limiting χ
2 distribution of goodness-of-fit statistics. A further set of routines is included that use parametric bootstrap methods to obtain confidence intervals (CIs) for model parameters and p-values. For this purpose, bootstrap distributions of parameter estimates and goodness-of-fit statistics are obtained from n samples of data. Each sample is generated by simulating the fitted model with parameter values estimated from the original data for the same task(s), stimulus levels, and trials per level as in the original data. Estimates and goodness-of-fit statistics are subsequently obtained for each sample, making up the bootstrap distributions. Bootstrap routines are designed to be discretionally used right after the call to the corresponding fitting routine, and their calling statement thus capitalizes on the substantial simplification that this permits. For the bootstrap routine that accompanies the fitting routine  , the calling statement in matlab is
, the calling statement in matlab is

where  is the output structure returned by
is the output structure returned by  (thus providing the necessary information about the model fitted to the original data, the choice of
(thus providing the necessary information about the model fitted to the original data, the choice of  , and
, and  , the estimated parameter values, and the values of the goodness-of-fit statistics) and
, the estimated parameter values, and the values of the goodness-of-fit statistics) and  , and
, and  are the data matrices that were submitted to
are the data matrices that were submitted to  to obtain
to obtain  (which is a convenient way of passing on to the bootstrap routine information about the number and values of stimulus levels and the number of trials per level in each task). Other arguments are as follows:
(which is a convenient way of passing on to the bootstrap routine information about the number and values of stimulus levels and the number of trials per level in each task). Other arguments are as follows:
-
 The number n of bootstrap samples to be generated (an integer scalar greater than 1).
The number n of bootstrap samples to be generated (an integer scalar greater than 1). -
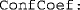 The confidence coefficient for CIs (a real scalar between 80 and 99.9).
The confidence coefficient for CIs (a real scalar between 80 and 99.9). -
 A logical scalar. When true, random number generators are initialized to a fixed seed, thus producing the same results whenever the same input arguments are given; when false, generators are initialized to a random seed, thus producing results subject to sampling error across repeated calls with the same input arguments.
A logical scalar. When true, random number generators are initialized to a fixed seed, thus producing the same results whenever the same input arguments are given; when false, generators are initialized to a random seed, thus producing results subject to sampling error across repeated calls with the same input arguments.
The calling statement and arguments in R are analogous. The output returned in  is a structure in MATLAB (see Fig. 6) and a list in R including a label for the problem (field 1), the model used in the simulation (field 2), the size of the bootstrap sample (field 3), the confidence coefficient for all CIs (field 4), triplets including the point estimate and upper and lower bounds of the CI for each of the model parameters (fields 5–25; for error or bias parameters not included in the fitted model, this triplet is returned as
is a structure in MATLAB (see Fig. 6) and a list in R including a label for the problem (field 1), the model used in the simulation (field 2), the size of the bootstrap sample (field 3), the confidence coefficient for all CIs (field 4), triplets including the point estimate and upper and lower bounds of the CI for each of the model parameters (fields 5–25; for error or bias parameters not included in the fitted model, this triplet is returned as  in MATLAB and as
in MATLAB and as  in R), and bootstrap p-values for the goodness-of-fit statistics X
2 and G
2 (fields 26–27).
in R), and bootstrap p-values for the goodness-of-fit statistics X
2 and G
2 (fields 26–27).
Output structure from the bootstrap routine for data in Fig. 1 and parameter values arising from the joint fit illustrated in Figs. 2 and 3. Fields 1–4 and the last two fields have similar content in output structures from all other bootstrap routines; only the number and content of the remaining fields vary according to the task(s) implied. For error or bias parameters not included in the simulated model, point estimates (which are always taken directly from the input to the bootstrap routine) and bootstrap CIs are returned as 
The calling statements for other bootstrap routines are simple modifications—namely,

In each case, the first argument is always an output structure/list returned by the applicable fitting routine. The output structures/lists  differ from that shown in Fig. 6 only as to the label for the problem in the first field and the set of parameters for which triplets are returned.
differ from that shown in Fig. 6 only as to the label for the problem in the first field and the set of parameters for which triplets are returned.
Manifest and latent performance measures
An additional routine is included that obtains performance measures (PSS, sensitivity, simultaneity boundaries, etc.) from the fitted curves through equations given in Appendix 1 in García-Pérez and Alcalá-Quintana (2012a). These measures are taken from the psychometric functions in Equations 5–7 after setting all error parameters to 0, an approach that is justifiable because these parameters help to account for data affected by response errors but do not contribute to a description of the processes governing the perception of temporal order (van Eijk et al., 2008, 2010). In addition to conventional performance measures, this routine can also provide latent measures defined in García-Pérez and Alcalá-Quintana (2012a). The MATLAB calling statement for this routine is

where  is a string (
is a string ( , or
, or  , case insensitive) that selects how the performance measures will be computed (see below),
, case insensitive) that selects how the performance measures will be computed (see below),  is a 1 × 2 vector that produces an annotated plot of the applicable psychometric functions within the given range (if no plot is desired, set
is a 1 × 2 vector that produces an annotated plot of the applicable psychometric functions within the given range (if no plot is desired, set  in MATLAB; in R, omit the argument), and the remaining arguments are (scalar) parameter values for use in computations. In MATLAB,
in MATLAB; in R, omit the argument), and the remaining arguments are (scalar) parameter values for use in computations. In MATLAB,  must be included even when TOJ is not selected, and
must be included even when TOJ is not selected, and  and
and  must also be included even when latent measures are requested; the input values in such cases are immaterial because they will not be used. In R, unnecessary arguments can be omitted. The routine returns a structure (or a list in R) whose fields vary with
must also be included even when latent measures are requested; the input values in such cases are immaterial because they will not be used. In R, unnecessary arguments can be omitted. The routine returns a structure (or a list in R) whose fields vary with  , as described next.
, as described next.
Performance measures for SJ2 tasks
The MATLAB script

(where  will not be used) with parameter values from Fig. 3, produces the graphical output shown in Fig. 7 and returns in
will not be used) with parameter values from Fig. 3, produces the graphical output shown in Fig. 7 and returns in  a structure with the following fields:
a structure with the following fields:
-
 Test-first simultaneity boundary (the 50% point on the left side of the psychometric function for S judgments).
Test-first simultaneity boundary (the 50% point on the left side of the psychometric function for S judgments). -
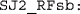 Reference-first simultaneity boundary (the 50% point on the right side of the psychometric function for S judgments).
Reference-first simultaneity boundary (the 50% point on the right side of the psychometric function for S judgments). -
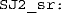 Simultaneity range (the distance between the two boundaries just described).
Simultaneity range (the distance between the two boundaries just described). -
 The midpoint between the two boundaries (one of the definitions of the PSS).
The midpoint between the two boundaries (one of the definitions of the PSS). -
 The peak of the psychometric function for S judgments (another definition of the PSS).
The peak of the psychometric function for S judgments (another definition of the PSS).
Note that the height of the psychometric function for S judgments in the SJ2 task may not exceed .5 (see García-Pérez & Alcalá-Quintana, 2012a). In these cases, boundaries do not exist according to the definition, and the first four fields thus return the string  .
.
Performance measures for SJ3 tasks
The Matlab script

(where  will not be used) also with parameter values from Fig. 3, produces the graphical output shown in Fig. 8 and returns in
will not be used) also with parameter values from Fig. 3, produces the graphical output shown in Fig. 8 and returns in  a structure with the following fields:
a structure with the following fields:
-
 Test-first simultaneity boundary (the crossing point of the psychometric functions for TF and S judgments).
Test-first simultaneity boundary (the crossing point of the psychometric functions for TF and S judgments). -
 Reference-first simultaneity boundary (the crossing point of the psychometric functions for S and RF judgments).
Reference-first simultaneity boundary (the crossing point of the psychometric functions for S and RF judgments). -
 Simultaneity range (the distance between the two boundaries just described).
Simultaneity range (the distance between the two boundaries just described). -
 The midpoint between the two boundaries (one of the definitions of the PSS).
The midpoint between the two boundaries (one of the definitions of the PSS). -
 The peak of the psychometric function for S judgments (another definition of the PSS).
The peak of the psychometric function for S judgments (another definition of the PSS). -
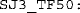 The 50% point on the psychometric function for TF judgments.
The 50% point on the psychometric function for TF judgments. -
 The 50% point on the psychometric function for RF judgments.
The 50% point on the psychometric function for RF judgments.
Note that the psychometric functions for TF and S judgments or the psychometric functions for S and RF judgments may not cross (see García-Pérez & Alcalá-Quintana, 2012a) and, in these cases, at least one of the boundaries does not exist. The applicable fields thus return the string  .
.
Performance measures for TOJ tasks
The MATLAB script

also with parameter values from Fig. 3, produces the graphical output shown in Fig. 9 and returns in  a structure with the following fields:
a structure with the following fields:
-
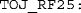 The 25% point on the psychometric function for RF responses.
The 25% point on the psychometric function for RF responses. -
 The 50% point on the psychometric function for RF responses (the PSS).
The 50% point on the psychometric function for RF responses (the PSS). -
 The 75% point on the psychometric function for RF responses.
The 75% point on the psychometric function for RF responses. -
 The size of the just noticeable difference (JND; the distance between the 50% and the 75% points).
The size of the just noticeable difference (JND; the distance between the 50% and the 75% points). -
 The distance between the 25% and the 75% points.
The distance between the 25% and the 75% points.
These measures always exist. Note that  uses the standard definition of JND, arising from the surmise that the psychometric function is odd symmetric about the PSS. Yet empirical data generally refute symmetry, a characteristic that our model accommodates (see García-Pérez & Alcalá-Quintana, 2012a). In these cases,
uses the standard definition of JND, arising from the surmise that the psychometric function is odd symmetric about the PSS. Yet empirical data generally refute symmetry, a characteristic that our model accommodates (see García-Pérez & Alcalá-Quintana, 2012a). In these cases,  (or half this value) is a more sensible measure of the JND.
(or half this value) is a more sensible measure of the JND.
This routine can also be used to remove response bias from performance measures. As is discussed in García-Pérez and Alcalá-Quintana (2012a), response bias (given by parameter ξ) unduly contaminates estimates of PSS and JND by affecting the location of the reference points for these measures. Thus, calling this routine with  returns the uncontaminated performance measures that would have arisen if the observer had shown no response bias.
returns the uncontaminated performance measures that would have arisen if the observer had shown no response bias.
Latent measures
The MATLAB script

(where neither  nor
nor  will be used) also with parameter values from Fig. 3, produces the graphical output shown in Fig. 10 and an output structure with the following fields:
will be used) also with parameter values from Fig. 3, produces the graphical output shown in Fig. 10 and an output structure with the following fields:
-
 The 50% point (i.e., the latent PSS) on the psychometric function for latent RF judgments if the observer had infinite resolution (i.e., as if δ = 0, even if the corresponding input parameter was not set to 0).
The 50% point (i.e., the latent PSS) on the psychometric function for latent RF judgments if the observer had infinite resolution (i.e., as if δ = 0, even if the corresponding input parameter was not set to 0). -
 The 15.87% point on the latent psychometric function.
The 15.87% point on the latent psychometric function. -
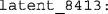 The 84.13% point on the latent psychometric function.
The 84.13% point on the latent psychometric function. -
 The distance between the 15.87% and the 84.13% points (a measure of sensitivity). Half this value is what the standard deviation would be if the psychometric function were a cumulative Gaussian.
The distance between the 15.87% and the 84.13% points (a measure of sensitivity). Half this value is what the standard deviation would be if the psychometric function were a cumulative Gaussian.
These measures also exist always.
Comparative analysis of performance in the MATLAB and R environments
All routines have been extensively tested using real and simulated data, and the accuracy with which they recover the generating parameters of simulated data varies only with the size of the data set (number of informative delay levels and number of trials per level; see García-Pérez & Alcalá-Quintana, 2012a, 2012b). However, the functions  and
and  implement different versions of the quasi-Newton algorithm, which may yield different solutions for the same data even when starting values are the same. To investigate this issue, 1,000 artificial data sets for each task were generated and submitted to the MATLAB and R routines in order to compare the solutions that they provide. To generate each data set, error model 1 was assumed, and random values for each of its 18 free parameters were independently drawn from uniform distributions on [1/80, 1/20] for λ
t and λ
r, on [−80, 80] for τ, on [20, 150] for δ (independently for each task), on [0, .1] for εTF, εS, and εRF (independently from one another and across tasks), and on [0, 1] for κTF-S, κS-TF, κRF-TF, and ξ (also independently from one another). These were used to simulate responses to SJ2, SJ3, and TOJ tasks with 100 trials at each of 15 delays (from −350 to 350 ms, in steps of 50 ms). The most demanding problem (i.e., the joint fit to data from the three tasks) was considered and MATLAB and R solutions for error model 1 were obtained. The agreement between the solutions across the 1,000 data sets was assessed through the concordance coefficient (Lin, 1989) for each of the estimated parameters.Footnote 8
implement different versions of the quasi-Newton algorithm, which may yield different solutions for the same data even when starting values are the same. To investigate this issue, 1,000 artificial data sets for each task were generated and submitted to the MATLAB and R routines in order to compare the solutions that they provide. To generate each data set, error model 1 was assumed, and random values for each of its 18 free parameters were independently drawn from uniform distributions on [1/80, 1/20] for λ
t and λ
r, on [−80, 80] for τ, on [20, 150] for δ (independently for each task), on [0, .1] for εTF, εS, and εRF (independently from one another and across tasks), and on [0, 1] for κTF-S, κS-TF, κRF-TF, and ξ (also independently from one another). These were used to simulate responses to SJ2, SJ3, and TOJ tasks with 100 trials at each of 15 delays (from −350 to 350 ms, in steps of 50 ms). The most demanding problem (i.e., the joint fit to data from the three tasks) was considered and MATLAB and R solutions for error model 1 were obtained. The agreement between the solutions across the 1,000 data sets was assessed through the concordance coefficient (Lin, 1989) for each of the estimated parameters.Footnote 8
Figure 11 shows scatterplots for selected parameters and also includes a summary panel giving the concordance coefficient for all 18 free parameters. The agreement between MATLAB and R estimates is excellent, with concordance coefficients (black circles in the summary panel at the bottom of Fig. 11) almost at unity for all parameters and only minimally lower for the bias parameters κ. The concordance coefficients between true parameter values and MATLAB estimates (blue circles in the summary panel of Fig. 11) or true parameter values and R estimates (red circles) are almost identical and usually very high with the exception of parameters εSJ2-S, εSJ3-S, and all κs. For a discussion of essential and inconsequential inaccuracies in the estimation of these parameters, see García-Pérez and Alcalá-Quintana (2012a, 2012b). Inaccuracies in the estimation of these parameters do not hamper the estimation of other parameters (most important, the psychologically relevant parameters λt, λr, τ, and δ).
Comparison of the outcomes of the routines in the MATLAB and R environments. The upper part shows scatterplots of estimates across environments for the parameters indicated in the insets. The lower panel gives the value of the concordance coefficient for each of the estimated parameters across environments (black circles) and, for reference, also gives the value of the concordance coefficient between true and estimated parameters in the R environment (red circles) and between true and estimated parameters in the MATLAB environment (blue circles)
The minor differences in parameter estimates across MATLAB and R implementations do not appear meaningful, neither by their magnitudes nor on consideration of the accompanying measures of goodness of fit. In fact, the agreement between goodness-of-fit tests was perfect across environments: The model was rejected at the .05 significance level by the X 2 statistic for 41 of the 1,000 cases according to MATLAB results and for the same cases according to R results; with the G 2 statistic, MATLAB results rejected the model for 89 cases and R results rejected the model for the same cases. This represents empirical rejection rates of 4.1% according to X 2 and 8.9% according to G 2. It should be noted that the nominal rejection rate is 5% given that the data were generated by the fitted model. Although G 2 is congruent with maximum-likelihood estimates and, thus, is the one that should in principle be used to assess the goodness of the fit (Collett, 2003, pp. 87–88; Read & Cressie, 1988), these results reveal that its small-sample behavior is inaccurate in the sense that it tends to reject a true model too often. The small-sample inaccuracy of G 2 is caused by its sensitivity to expected frequencies that are too low when observed frequencies are nonnull (García-Pérez & Núñez-Antón, 2001, 2004), a characteristic that is somewhat common in the analysis of SJ and TOJ data (i.e., small probabilities of S and RF responses at long negative delays, and also small probabilities of S and TF responses at long positive delays). In contrast, X 2 is less sensitive to small expectations, and its accuracy in small-sample conditions has also been documented (García-Pérez, 1994). Our fitting routines nevertheless compute and return both statistics for them to be employed at the user’s discretion, but recall that the bootstrap routines described above also provide bootstrap p-values that are not affected by these problems.
Final comments
Implementation details and usage recommendations for fitting routines
The MATLAB routines disable the inconsequential warnings of  and
and  that are frequent when error model 0 is fitted or when the data include large numbers of cells with null counts.Footnote 9 These messages are enabled again before returning.
that are frequent when error model 0 is fitted or when the data include large numbers of cells with null counts.Footnote 9 These messages are enabled again before returning.
Intermediate iterations within  can occasionally use points that lie out of the bounds of the parameter space, which may produce, for example, negative probabilities and, in turn, unexpected results (see documentation at http://www.mathworks.com/help/toolbox/optim/ug/fmincon.html). This is also true for the L-BFGS-B method in the R function
can occasionally use points that lie out of the bounds of the parameter space, which may produce, for example, negative probabilities and, in turn, unexpected results (see documentation at http://www.mathworks.com/help/toolbox/optim/ug/fmincon.html). This is also true for the L-BFGS-B method in the R function  , although this is not documented in the R Reference Manual. The objective function is thus written so as to check first for the feasibility of the current point, applying a large penalty (a negative log-likelihood of 1e + 20) without any further computation if the current point is infeasible. The same large penalty replaces negative log-likelihood values of infinity that occur when one or more of the probabilities in the log-likelihood function is zero.
, although this is not documented in the R Reference Manual. The objective function is thus written so as to check first for the feasibility of the current point, applying a large penalty (a negative log-likelihood of 1e + 20) without any further computation if the current point is infeasible. The same large penalty replaces negative log-likelihood values of infinity that occur when one or more of the probabilities in the log-likelihood function is zero.
Recall that N SJ2, N SJ3, and N TOJ stand for the number of delays at which SJ2, SJ3, and TOJ data were collected, respectively. The number of independent data sources for the separate fit of SJ2, SJ3, and TOJ data are, thus, N SJ2, 2N SJ3, and N TOJ, respectively. Sufficient degrees of freedom exist to test the fit of error model 1 separately to SJ2, SJ3, or TOJ data as long as N SJ2 > 7, N SJ3 > 5, or N TOJ > 7, respectively. These considerations straightforwardly extend to error models involving fewer free parameters and to the joint fit to data from two or three tasks (e.g., sufficient degrees of freedom for testing the joint fit of error model 1 to data from the three tasks exist if N SJ2 + 2N SJ3 + N TOJ > 18). It is unlikely that an experiment will be planned to collect data at fewer delays, but in such a case, the routines report that the number of degrees of freedom is insufficient. Estimated parameters are meaningful even if N SJ2, N SJ3, or N TOJ are too small by the degrees-of-freedom criterion.
The overall number of multidimensional starting points for the search within  and
and  is the product of the lengths of the input arguments providing starting values. This is fixed regardless of the number of parameters that some of these arguments refer to—that is, the three response error parameters εTF, εS, and εRF to which
is the product of the lengths of the input arguments providing starting values. This is fixed regardless of the number of parameters that some of these arguments refer to—that is, the three response error parameters εTF, εS, and εRF to which  applies or the four bias parameters (ξ, κTF-S, κS-TF, and κRF-TF,) to which
applies or the four bias parameters (ξ, κTF-S, κS-TF, and κRF-TF,) to which  applies. This implies that starting values are not crossed for parameters with the same referent and this also holds for the two or three δs that are estimated when the model is fitted jointly to data from two or three tasks. Our decision prevents an exponential increase in the number of multidimensional starting points as the number of free parameters increases from just four (when error model 0 is fitted to SJ2 data) to 18 (when error model 1 is jointly fitted to data from the three tasks), and its adequacy was confirmed in extensive simulation studies. In the interest of efficiency, multiple starting values are ignored for parameters that will not be estimated as a result of the choice of an error model (e.g., multiple values in
applies. This implies that starting values are not crossed for parameters with the same referent and this also holds for the two or three δs that are estimated when the model is fitted jointly to data from two or three tasks. Our decision prevents an exponential increase in the number of multidimensional starting points as the number of free parameters increases from just four (when error model 0 is fitted to SJ2 data) to 18 (when error model 1 is jointly fitted to data from the three tasks), and its adequacy was confirmed in extensive simulation studies. In the interest of efficiency, multiple starting values are ignored for parameters that will not be estimated as a result of the choice of an error model (e.g., multiple values in  when error model 0 is selected).
when error model 0 is selected).
Once a solution for each starting point has been obtained, the routines initially select the solution that is best by the likelihood criterion. This solution is always returned when the estimates of λ
t or λ
r do not lie at the upper bound defined in  . When any of them lies at that upper bound, the routines seek the best solution for which boundary estimates did not occur; if the associated log-likelihood of this alternative solution does not exceed by 0.5% the log-likelihood of the best solution, this alternative solution is returned instead. Technical details and further recommendations for handling these cases are given in Appendix 1. On the assumption that
. When any of them lies at that upper bound, the routines seek the best solution for which boundary estimates did not occur; if the associated log-likelihood of this alternative solution does not exceed by 0.5% the log-likelihood of the best solution, this alternative solution is returned instead. Technical details and further recommendations for handling these cases are given in Appendix 1. On the assumption that  and
and  are declared as suggested earlier (i.e., effectively unbounded), boundary estimates for τ and δ are not checked for.
are declared as suggested earlier (i.e., effectively unbounded), boundary estimates for τ and δ are not checked for.
An important aspect of usage is how many and which particular starting values should be provided for each parameter. In our examples, delay levels are given in milliseconds, and the particular starting values that we used for parameters λ
t, λ
r, τ, and δ are appropriate in those units, but these starting values should be scaled accordingly if other units are used.Footnote 10 All the real and artificial data with which the routines were tested share with the data in Fig. 1 that the relevant action takes place in a range of delays roughly between −400 and 400 ms. For such data, and with the only exception to be discussed below, different starting values generally yield almost the same final solution, as can be seen in the progress information provided when the logical argument  is set true. The sets of starting values used in the previous examples thus turn out to represent too broad a choice: Actually, the R routines typically render the same solution for all starting values, whereas MATLAB routines are slightly sensitive to starting value when run under pre-2010 releases. We have come across no cases in which providing more than a single starting value in
is set true. The sets of starting values used in the previous examples thus turn out to represent too broad a choice: Actually, the R routines typically render the same solution for all starting values, whereas MATLAB routines are slightly sensitive to starting value when run under pre-2010 releases. We have come across no cases in which providing more than a single starting value in  or
or  was useful, and the success at finding the optimal solution did not vary with the particular value given (provided that
was useful, and the success at finding the optimal solution did not vary with the particular value given (provided that  does not exceed about .75 in R). This is the reason why single starting values for these parameters were used in our examples. On the other hand, the use of single starting values for parameters τ and δ also proved sufficient in most cases, although using two starting values for each of these parameters (and also two starting values for λt and λr, as in our examples) is a safeguard that does no harm: The sets of starting values in our examples expand into 16 multidimensional starting points for which the most demanding problem (fitting error model 1 jointly to data from the three tasks) completes within a few seconds (8–10 s for the MATLAB routine on the 2008 PC where we ran our tests; 25–30 s for the R routine). Users may want to set true the logical argument
does not exceed about .75 in R). This is the reason why single starting values for these parameters were used in our examples. On the other hand, the use of single starting values for parameters τ and δ also proved sufficient in most cases, although using two starting values for each of these parameters (and also two starting values for λt and λr, as in our examples) is a safeguard that does no harm: The sets of starting values in our examples expand into 16 multidimensional starting points for which the most demanding problem (fitting error model 1 jointly to data from the three tasks) completes within a few seconds (8–10 s for the MATLAB routine on the 2008 PC where we ran our tests; 25–30 s for the R routine). Users may want to set true the logical argument  so as to gather evidence about the dependence of the final solution on starting value, which actually provides useful diagnostic information (see below). It is also useful to develop the habit of setting true the logical argument
so as to gather evidence about the dependence of the final solution on starting value, which actually provides useful diagnostic information (see below). It is also useful to develop the habit of setting true the logical argument  and searching for visible signs that the optimal solution may not have been found with the given starting values. Should this happen, we would recommend that users replace and try out, one at a time, alternative pairs of starting values for λt, λr, τ, and δ that are more narrowly confined within specific subregions of the parameter space. In our experience, taking this action is very rarely needed in MATLAB and never needed in R.
and searching for visible signs that the optimal solution may not have been found with the given starting values. Should this happen, we would recommend that users replace and try out, one at a time, alternative pairs of starting values for λt, λr, τ, and δ that are more narrowly confined within specific subregions of the parameter space. In our experience, taking this action is very rarely needed in MATLAB and never needed in R.
The exception mentioned above occurs only on fitting error model 0 in MATLAB and reveals a dependence on starting values that is easy to deal with. To illustrate it, consider the script

which produces the following output on the command window (as a result of  ):
):

Note that values of 1e + 20 occur for the objective function in the presumed optimal solution for half of the starting points. Across the board, however, a meaningful solution is found for the remaining starting points, and the best of them fits the data adequately (asymptotic p-values for the X
2 and G
2 statistics were .6427 and .3987, respectively; see also Fig. 12). Values of 1e + 20 in the objective function (our replacement for values of infinity, as discussed above) at the final solution are a result of the combined effect of two factors. First, with large values for λt and λr, theoretical probabilities for some responses are zero under error model 0 at some delay levels (e.g., for RF or S responses at very long negative delays, and for TF or S responses at very long positive delays). Second, this will certainly occur for starting points involving these large values (i.e., at the candidate solution in the first iteration) and in a way that the same outcome occurs also when  explores alternative candidate solutions in feasible directions. This makes
explores alternative candidate solutions in feasible directions. This makes  halt and return without even iterating on the presumption that a minimum has been found, and not because the value of the objective function is small but because it does not change for candidate points in feasible directions. The L-BFGS-B algorithm in the R function
halt and return without even iterating on the presumption that a minimum has been found, and not because the value of the objective function is small but because it does not change for candidate points in feasible directions. The L-BFGS-B algorithm in the R function  seems to be free of this problem. The easy way around this problem in MATLAB consists of avoiding relatively large starting values for λt and λr (i.e., the value 1/10 in our example). Thus, setting
seems to be free of this problem. The easy way around this problem in MATLAB consists of avoiding relatively large starting values for λt and λr (i.e., the value 1/10 in our example). Thus, setting  and
and  produces virtually the same solution for all 16 starting points, coinciding also with the solution that was found in our initial example for the second and third starting values. Although which starting values for λt and λr are too large depends on the data, improper values of 1e + 20 in the objective function at the final solution actually identify them.
produces virtually the same solution for all 16 starting points, coinciding also with the solution that was found in our initial example for the second and third starting values. Although which starting values for λt and λr are too large depends on the data, improper values of 1e + 20 in the objective function at the final solution actually identify them.
Choice of a model for response errors
Error model 1 is the most general, and we recommend that users fit this model first, setting true the logical input variables  and
and  so as to gather evidence on the appropriateness of the number and values of starting points that were provided. This may also yield estimates of error parameters (εTF, εS, and εRF for the applicable task) that are nearly zero and, thus, compatible with a simpler version of the general model. In these cases, a rerun seeking to fit the specific model suggested by the initial results for error model 1 allows a test between the two models, given that the output structure/list always includes the BIC of the fitted model. The G
2 statistic included in the output structure/list can alternatively be used for model comparisons (for details, see Collett, 2003, Sections 3.9–3.11). Indeed, the model selected according to the BIC is rather often rejected according to conventional goodness-of-fit statistics, whereas competing models with only a slightly larger BIC often pass goodness-of-fit tests (see García-Pérez & Alcalá-Quintana, 2012a).
so as to gather evidence on the appropriateness of the number and values of starting points that were provided. This may also yield estimates of error parameters (εTF, εS, and εRF for the applicable task) that are nearly zero and, thus, compatible with a simpler version of the general model. In these cases, a rerun seeking to fit the specific model suggested by the initial results for error model 1 allows a test between the two models, given that the output structure/list always includes the BIC of the fitted model. The G
2 statistic included in the output structure/list can alternatively be used for model comparisons (for details, see Collett, 2003, Sections 3.9–3.11). Indeed, the model selected according to the BIC is rather often rejected according to conventional goodness-of-fit statistics, whereas competing models with only a slightly larger BIC often pass goodness-of-fit tests (see García-Pérez & Alcalá-Quintana, 2012a).
As an alternative to such a step-by-step approach, the option  was implemented for automated exploration of all possible models for the case on hand. Users must be aware that this option slows down execution. For instance, use of this option with
was implemented for automated exploration of all possible models for the case on hand. Users must be aware that this option slows down execution. For instance, use of this option with  implies that an overall number of 8 × 8 × 4 = 256 alternative models (see Table 1) must be evaluated. If 16 multidimensional starting points are used as in our examples, execution time will be multiplied roughly by a factor of 256. For the more common cases in which a model is fitted to data from a single task, the option
implies that an overall number of 8 × 8 × 4 = 256 alternative models (see Table 1) must be evaluated. If 16 multidimensional starting points are used as in our examples, execution time will be multiplied roughly by a factor of 256. For the more common cases in which a model is fitted to data from a single task, the option  does not result in a large increase in execution time, since only eight models (for SJ tasks) or four models (for TOJ tasks) are implied.
does not result in a large increase in execution time, since only eight models (for SJ tasks) or four models (for TOJ tasks) are implied.
Implementation details and usage recommendations for bootstrap routines
The cost of running bootstrap routines varies across them (the slowest is naturally  and the fastest are
and the fastest are  , and
, and  ), but costs also vary across error models. In MATLAB, the cost per bootstrap sample ranges between 0.03 s (for
), but costs also vary across error models. In MATLAB, the cost per bootstrap sample ranges between 0.03 s (for  under error model 0) and 0.40 s (for
under error model 0) and 0.40 s (for  under error model 1); the cost is 2–3 times as large in R. Our tests revealed that setting
under error model 1); the cost is 2–3 times as large in R. Our tests revealed that setting  generally renders sufficiently accurate CIs and p-values, in the sense that the returned results do not change meaningfully for larger bootstrap samples. Users may nevertheless want to check out with small bootstrap samples how long the routine of concern takes to complete on their platform, and then use this information to set
generally renders sufficiently accurate CIs and p-values, in the sense that the returned results do not change meaningfully for larger bootstrap samples. Users may nevertheless want to check out with small bootstrap samples how long the routine of concern takes to complete on their platform, and then use this information to set  to the largest sensible value. The upper and lower limits of CIs are obtained from the bootstrap distributions through the MATLAB function
to the largest sensible value. The upper and lower limits of CIs are obtained from the bootstrap distributions through the MATLAB function  or the R function
or the R function  .
.
All bootstrap routines issue a message to the console each time an additional 10% of their workload has been completed. These routines expend negligible time generating the requested  data sets, and most of the execution time is then taken by the process of estimating model parameters for each bootstrap sample. To speed up the operation of these routines, parameter estimation uses a single starting point at the actual parameter values of the generating model. It is generally believed that this strategy facilitates parameter recovery, although no evidence to this effect seems to have ever been reported. We should stress that this potential evil has no bearing on the purposes of these routines.
data sets, and most of the execution time is then taken by the process of estimating model parameters for each bootstrap sample. To speed up the operation of these routines, parameter estimation uses a single starting point at the actual parameter values of the generating model. It is generally believed that this strategy facilitates parameter recovery, although no evidence to this effect seems to have ever been reported. We should stress that this potential evil has no bearing on the purposes of these routines.
Bootstrap routines generate data sets under the method of constant stimuli (MOCS), that is, for fixed numbers of trials at each of a fixed set of stimulus levels as implied in the input arguments  , and
, and  . This is the most common method by which data are gathered in research on timing judgments, but the use of adaptive methods has occasionally been reported (e.g., Yarrow et al., 2011). It should be noted that bootstrap distributions of parameter estimates and goodness-of-fit measures vary meaningfully across psychophysical methods (García-Pérez & Alcalá-Quintana, 2005) and, hence, CIs and p-values returned by our bootstrap routines can only be regarded as approximations if the original data were collected with a psychophysical method other than MOCS.
. This is the most common method by which data are gathered in research on timing judgments, but the use of adaptive methods has occasionally been reported (e.g., Yarrow et al., 2011). It should be noted that bootstrap distributions of parameter estimates and goodness-of-fit measures vary meaningfully across psychophysical methods (García-Pérez & Alcalá-Quintana, 2005) and, hence, CIs and p-values returned by our bootstrap routines can only be regarded as approximations if the original data were collected with a psychophysical method other than MOCS.
Protection against misuse
Our fitting routines are protected against invalid input such as illegal values for the argument  . Similarly, the routines check that data matrices have the required size, that
. Similarly, the routines check that data matrices have the required size, that  , and
, and  are two-element vectors satisfying the constraints on these parameters, that arguments providing starting values do not contain illegal values, and that
are two-element vectors satisfying the constraints on these parameters, that arguments providing starting values do not contain illegal values, and that  and
and  are logical scalars. The routines also check that values in response rows (from second to last) of the matrices SJ2data, SJ3data, and TOJdata are nonnegative. If any of these checks fails, the routines return with an informative error message without attempting any computation. Out-of-bounds starting values for bounded parameters are replaced by interior points within the search space directly by
are logical scalars. The routines also check that values in response rows (from second to last) of the matrices SJ2data, SJ3data, and TOJdata are nonnegative. If any of these checks fails, the routines return with an informative error message without attempting any computation. Out-of-bounds starting values for bounded parameters are replaced by interior points within the search space directly by  in the MATLAB routines, or actively by our R routines (which issue warning messages in such cases).
in the MATLAB routines, or actively by our R routines (which issue warning messages in such cases).
However, fitting routines cannot be protected against an inadequate arrangement of the response rows of matrices  , or
, or  , since this event is actually difficult to identify with certainty. Users must thus be cautious in creating these matrices, although the outcome of the routines is perfectly predictable in case of errors that do not affect the first row (delay levels): They will return large values for error parameters because the data will be interpreted as if judgments had been massively misreported in some form, without affecting the estimates of the remaining parameters. As is shown in Fig. 13, errors in the arrangement of response rows within the matrices should be easy to spot out from the plots produced by the routines, which label data points and curves assuming that response rows are arranged as illustrated in Fig. 1. Errors such that the delay levels are not stored in the first row of the data matrices will produce unpredictable results if only positive delays were involved. Note also that only the order of the rows is relevant: The routines do not require the columns of the data matrices to be arranged so that delay level increases from left to right.
, since this event is actually difficult to identify with certainty. Users must thus be cautious in creating these matrices, although the outcome of the routines is perfectly predictable in case of errors that do not affect the first row (delay levels): They will return large values for error parameters because the data will be interpreted as if judgments had been massively misreported in some form, without affecting the estimates of the remaining parameters. As is shown in Fig. 13, errors in the arrangement of response rows within the matrices should be easy to spot out from the plots produced by the routines, which label data points and curves assuming that response rows are arranged as illustrated in Fig. 1. Errors such that the delay levels are not stored in the first row of the data matrices will produce unpredictable results if only positive delays were involved. Note also that only the order of the rows is relevant: The routines do not require the columns of the data matrices to be arranged so that delay level increases from left to right.
Output from the routine that fits the model jointly to data from the three tasks when rows 2 and 3 in  and
and  from Fig. 1 were swapped, whereas
from Fig. 1 were swapped, whereas  was left intact. The presumed S data in the left panel have the shape of the actual A data that they represent, and the presumed RF data in the right panel have the shape of the actual TF data that they represent. The routines render parameter estimates virtually identical to those shown in Fig. 3, with differences only in the response error parameters for SJ2 and TOJ tasks: For SJ2 data, estimates of εTF, εS, and εRF are, respectively, .9788, .9407, and .9239, implying that the data are interpreted as if judgments had been massively misreported; for TOJ data, estimates of εTF and εRF are, respectively, .9859 and .9891, also implying that the data are interpreted as if judgments had been massively misreported. Response error parameters for SJ3 data remained as in Fig. 3. This example shows the robustness of the routines to large differences between the starting value for error parameters (defined as
was left intact. The presumed S data in the left panel have the shape of the actual A data that they represent, and the presumed RF data in the right panel have the shape of the actual TF data that they represent. The routines render parameter estimates virtually identical to those shown in Fig. 3, with differences only in the response error parameters for SJ2 and TOJ tasks: For SJ2 data, estimates of εTF, εS, and εRF are, respectively, .9788, .9407, and .9239, implying that the data are interpreted as if judgments had been massively misreported; for TOJ data, estimates of εTF and εRF are, respectively, .9859 and .9891, also implying that the data are interpreted as if judgments had been massively misreported. Response error parameters for SJ3 data remained as in Fig. 3. This example shows the robustness of the routines to large differences between the starting value for error parameters (defined as  in the calling sequence) and its final value in the solution for SJ2 and TOJ data, and also shows the robustness of a common starting value for all error parameters despite large differences in the final solution across individual parameters (i.e., large final values for SJ2 and TOJ data, along with small final values for SJ3 data)
in the calling sequence) and its final value in the solution for SJ2 and TOJ data, and also shows the robustness of a common starting value for all error parameters despite large differences in the final solution across individual parameters (i.e., large final values for SJ2 and TOJ data, along with small final values for SJ3 data)
Bootstrap routines are similarly protected, and they also check that the content of the first field of their first argument (a structure/list, as described above) matches what the applicable fitting routine would have placed there. However, bootstrap routines cannot possibly check whether the first input arguments (output structure/list from the fitting routine and data matrices) actually go together. In case of mismatch, the bootstrap results will apply to the parameter estimates in the structure/list given in the first argument, but under the number and values of stimulus levels and the number of trials per level indicated by the data matrices given in the subsequent arguments.
Routine  is also protected, and it simply returns with an informative error message if the string
is also protected, and it simply returns with an informative error message if the string  has an invalid value, if arguments providing parameter values are not real scalars or contain illegal values (e.g., negative λ
r, λ
t, or δ, ξ < 0, or ξ > 1), or if the content of
has an invalid value, if arguments providing parameter values are not real scalars or contain illegal values (e.g., negative λ
r, λ
t, or δ, ξ < 0, or ξ > 1), or if the content of  is invalid—that is, it is neither an empty vector (only in MATLAB) nor a 1 × 2 vector defining a nonnull range. This routine will produce the requested plot even if the specified range for the plot is not in the same units as the input parameter values (e.g., a plot range given in milliseconds when parameter values were estimated for delay levels given in seconds, or vice versa). The functions will still be plotted correctly, but over an inadequate range.
is invalid—that is, it is neither an empty vector (only in MATLAB) nor a 1 × 2 vector defining a nonnull range. This routine will produce the requested plot even if the specified range for the plot is not in the same units as the input parameter values (e.g., a plot range given in milliseconds when parameter values were estimated for delay levels given in seconds, or vice versa). The functions will still be plotted correctly, but over an inadequate range.
Limitations
All the MATLAB results reported here were obtained under version 7.4.0.287 (release 2007a). The routines have also been tested under versions 7.0.0.19920 (release 14), 7.9.0.529 (release 2009b), and 7.11.1.866 (release 2010b, Service Pack 1), with no meaningful differences in the outcomes except that the most recent versions (i.e., those using  ) are substantially less sensitive to starting valueFootnote 11 and minimally slower. The R routines were tested under versions 2.14.0 (released 2011-10-31) and 2.15.1 (released 2012-06-22). We do not expect the routines to perform differently under newer versions unless the functions
) are substantially less sensitive to starting valueFootnote 11 and minimally slower. The R routines were tested under versions 2.14.0 (released 2011-10-31) and 2.15.1 (released 2012-06-22). We do not expect the routines to perform differently under newer versions unless the functions  or
or  change in some meaningful way.
change in some meaningful way.
The model that the routines fit is valid under the most common situations in which simultaneity and temporal-order judgments are collected with point stimuli. The characteristics of this type of data are inverted-U shaped S data and monotonicity of TF and RF data (except for departures that can be reasonably attributed to response errors; see García-Pérez & Alcalá-Quintana, 2012a, 2012b). Two cases in which these characteristics do not occur are worth pointing out. One of them is in experiments that cause temporal-order judgments to reverse at short delays (as is the case with mechanical stimulation with crossed hands; see Yamamoto & Kitazawa, 2001), which render N-shaped RF data. The other is with repetitive stimulus trains for which TF, S, and RF data show wavy patterns arising from the fact that delays that are multiples of the period of the train actually render matched trains despite the nominal delay (see, e.g., Petrini, Holt, & Pollick, 2010). These cases are not covered by our routines, because they imply models that substantially differ from one another and also from the model adopted here. Implementation of such models thus requires entirely different routines.
Users must be aware that not all data sets are suitable for fitting psychometric functions and the use of these routines (or others, for that matter) with unsuitable data may yield inaccurate parameter estimates. For instance, data may be collected with adaptive methods, which are currently rarely used in research on time perception but which may eventually become popular. The consequence of their use is that stimulus levels around the central region of the psychometric function are tried very often, whereas stimulus levels in outer regions are rarely tried, if at all. The resultant data provide precise information about the location of the PSS, but very little information that is useful for estimating the remaining parameters of the psychometric function. Attempts to fit psychometric functions to data gathered with adaptive methods generally yield inaccurate estimates (see García-Pérez & Alcalá-Quintana, 2005), since no routine fitting any model can make up for a lack of information in the data.
MOCS is the most common method used in research on time perception, but its use may also yield data that are unsuitable for fitting psychometric functions of any kind. The most important design problem of MOCS is that the range and spacing of stimulus levels must be fixed in advance and it may turn out to be inadequate for some of the participants or some of the experimental conditions. One of the forms in which the choice of stimulus levels may be inadequate is when it turns out to be too broad, so that asymptotic performance is observed at a relatively large number of stimulus levels on either end of the stimulus range. The consequence is that data collected at these outer ends are not informative, leaving only a small subset of stimulus levels that provide useful but scarce information for an accurate estimation of the psychometric function. For an empirical example and analysis of this situation, see Appendix 3 in García-Pérez and Alcalá-Quintana (2012a). The other form in which MOCS ranges may be inadequate is when they turn out to be too narrow, also failing to sample the psychometric function properly and in full. In either of these cases, and also if the number of trials per SOA is very small, parameter estimation will be compromised, whether parameters are estimated with the routines described here or with software fitting alternative psychometric functions. Little can be done if evidence of inadequate stimulus ranges reveals itself once the data have been collected, but the breadth of the CIs provided by the bootstrap routines included in our package will indicate how dependable the results are.
It should also be noted that general recommendations as to how many SOAs to sample and how many trials per SOA to administer for accurate parameter estimation cannot be given. The crucial aspect is whether the data are informative: Administering many trials at uninformative or misplaced SOAs is useless. Nevertheless, simulation results reported elsewhere (García-Pérez & Alcalá-Quintana, 2012a, 2012b), as well as other unpublished simulation results, suggest that when SOAs are placed at informative levels, 15–20 trials at each of 10–12 SOAs render sufficiently informative data for accurate point estimation and narrow CIs for the SJ3 task in isolation. The same sampling plan achieves similar accuracy under isolated SJ2 tasks, but some more trials per SOA are necessary under isolated TOJ tasks (see Appendix 2 for some representative results). These requirements are thoroughly analogous to those under which fitting Gaussian or logistic functions to data return dependable estimates (see García-Pérez & Alcalá-Quintana, 2005).
Notes
It should be stressed that researchers must use their own discretion to decide whether data from two or three tasks with the same observers, stimuli, and conditions should be fitted jointly (i.e., with common sensory parameters across tasks) or separately. Our software includes routines that allow carrying out the estimation in both ways. An anonymous reviewer pointed out that issues such as practice, fatigue, time-on-task, time of day, or others may produce differences in true sensory parameters. This is correct, but other things being equal, the only reason why these factors would differentially affect the various tasks (thus advising against joint estimation) is if they were not adequately controlled by the experimenter. Any suspicion that these extraneous variables have contaminated the data should prompt researchers not only to avoid joint estimation, but to avoid estimation at all. Without proper experimental control of extraneous variables, research validity is seriously compromised, and no approach to parameter estimation or data analysis can remove contamination from the data.
In R, the function
 is called with the option
is called with the option  as the choice of algorithm. In MATLAB, the function
as the choice of algorithm. In MATLAB, the function  is part of the Optimization Toolbox, and we chose to use it because the function
is part of the Optimization Toolbox, and we chose to use it because the function  available in the basic MATLAB package uses only the Nelder–Mead algorithm, which proved to be nondependable in this particular application. The function
available in the basic MATLAB package uses only the Nelder–Mead algorithm, which proved to be nondependable in this particular application. The function  has changed over releases, mostly in what regards the default and available optimization algorithms. For this reason, the routines check the running version and set options for
has changed over releases, mostly in what regards the default and available optimization algorithms. For this reason, the routines check the running version and set options for  as follows. For releases dated 2007 or earlier, the option
as follows. For releases dated 2007 or earlier, the option  is set to
is set to  ; for releases dated 2008 or 2009, the new option
; for releases dated 2008 or 2009, the new option  is set to
is set to  ; for releases dated 2010 or later, the option
; for releases dated 2010 or later, the option  is set to the new value
is set to the new value  .
.The meaning of the output flag in field 2 varies across versions of MATLAB due to the different algorithms implied. Users are referred to the help documentation for
 in their installation.
in their installation.The second of these fields gains meaning when the user selects
 because then this field will indicate which model turned out to be the best.
because then this field will indicate which model turned out to be the best.This information is important for judging the validity of the omnibus goodness-of-fit test and the amount of evidence that it provides against the model. Note that each delay level (i.e., each column in the data matrix for the applicable task in Fig. 2) contributes one (for SJ2 and TOJ data) or two (for SJ3 data) degrees of freedom to the omnibus goodness-of-fit statistic, and recall also that each free parameter that is estimated subtracts one degree of freedom from the overall count. If the expected frequency in one of the cells in a column is too low—say, 0.03—when the observed frequency is only 1, the contribution of that single cell to the chi-square statistic is 0.972/0.03 = 31.36, a value that is by itself above the critical limit for a .05-size test with 19 degrees of freedom. This single contribution would suffice to reject the model if data had been collected at nine delays (which yields 18 degrees of freedom under error model 1), even if the expected frequencies in all remaining cells were exactly identical to the observed frequencies. This is an example of a spurious rejection caused by very low expected frequencies when the observed frequency is not null. Had the observed frequency been null, the contribution 0.032/0.03 = 1 would not have caused a rejection.
Strictly speaking, error parameters not included in the model are implicitly assumed to be valued at 0. We decided to return them as NaN (or NA) instead so as to differentiate this case from those in which one or more error parameters are included in the model and their estimated value(s) turn out to be 0.
Recall that in model comparisons, the model with the lowest BIC is the best-fitting model.
The concordance coefficient is the standard statistic to assess agreement, since it measures the tightness of data points around the diagonal identity line in a scatterplot.
These warnings are no longer issued in the most recent versions of MATLAB.
For instance, if delay levels were given in seconds, the current starting values for parameters λt and λr would have to be multiplied by 1,000, whereas the current starting values for parameters τ and δ would have to be divided by 1,000. The current bounds for parameters λt and λr would also have to be multiplied by 1,000. We have checked out that scaling the units with which time is measured does not affect the performance of the routines in any respect, but, to avoid messing with the numerical scale of starting values and bounds, we would recommend users to give delay levels always in milliseconds.
For the example given above in which half of the starting values returned an improper value of 1e + 20 for the objective function at the final solution, release 2010b reproduced this outcome but, in contrast, the value of the objective function at the solution for each and all of the eight remaining starting values was 1220.1251, a value that is attained only for two of those eight starting values in the illustration given above.
References
Collett, D. (2003). Modelling Binary Data (2nd ed.). Boca Raton, FL: CRC Press.
Colonius, H., & Diederich, A. (2011). Computing an optimal time window of audiovisual integration in focused attention tasks: Illustrated by studies on effect of age and prior knowledge. Experimental Brain Research, 212, 327–337. doi:10.1007/s00221-011-2732-x
Diederich, A., & Colonius, H. (2011). Modeling multisensory processes in saccadic responses: Time-window-of-integration model. In M. M. Murray & M. T. Wallace (Eds.), The Neural Bases of Multisensory Processes (pp. 253–276). Boca Raton, FL: CRC Press.
Fujisaki, W., & Nishida, S. (2009). Audio–tactile superiority over visuo–tactile and audio–visual combinations in the temporal resolution of synchrony perception. Experimental Brain Research, 198, 245–259. doi:10.1007/s00221-009-1870-x
García-Pérez, M. A. (1994). Parameter estimation and goodness-of-fit testing in multinomial models. British Journal of Mathematical and Statistical Psychology, 47, 247–282. doi:10.1111/j.2044-8317.1994.tb01037.x
García-Pérez, M. A. (2000). Optimal setups for forced-choice staircases with fixed step sizes. Spatial Vision, 13, 431–448. doi:10.1163/156856800741306
García-Pérez, M. A. (2001). Yes-no staircases with fixed step sizes: Psychometric properties and optimal setup. Optometry and Vision Science, 78, 56–64. doi:10.1097/00006324-200101010-00015
García-Pérez, M. A., & Alcalá-Quintana, R. (2005). Sampling plans for fitting the psychometric function. Spanish Journal of Psychology, 8, 256–289. http://www.ucm.es/info/Psi/docs/journal/v8_n2_2005/art256.pdf
García-Pérez, M. A., & Alcalá-Quintana, R. (2012a). On the discrepant results in synchrony judgment and temporal-order judgment tasks: A quantitative model. Psychonomic Bulletin & Review, 19, 820–846. doi:10.3758/s13423-012-0278-y
García-Pérez, M. A., & Alcalá-Quintana, R. (2012b). Response errors explain the failure of independent-channels models of perception of temporal order. Frontiers in Psychology – Perception Science, 3, 94. doi:10.3389/fpsyg.2012.00094
García-Pérez, M. A., & Núñez-Antón, V. (2001). Small-sample comparisons for power-divergence goodness-of-fit statistics for symmetric and skewed simple null hypotheses. Journal of Applied Statistics, 28, 855–874. doi:10.1080/02664760120074942
García-Pérez, M. A., & Núñez-Antón, V. (2004). Small-sample comparisons for goodness-of-fit statistics in one-way multinomials with composite hypotheses. Journal of Applied Statistics, 31, 161–181. doi:10.1080/0266476032000148849
Heath, R. A. (1984). Response time and temporal order judgement in vision. Australian Journal of Psychology, 36, 21–34. doi:10.1080/00049538408255075
Keetels, M., & Vroomen, J. (2008). Temporal recalibration to tactile–visual asynchronous stimuli. Neuroscience Letters, 430, 130–134. doi:10.1016/j.neulet.2007.10.044
Lin, L. I.-K. (1989). A concordance correlation coefficient to evaluate reproducibility. Biometrics, 45, 255–268. doi:10.2307/2532051
Petrini, K., Holt, S. P., & Pollick, F. (2010). Expertise with multisensory events eliminates the effect of biological motion rotation on audiovisual synchrony perception. Journal of Vision, 10(5):2, 1–14. doi:10.1167/10.5.2
Read, T. R. C., & Cressie, N. A. C. (1988). Goodness-of-Fit Statistics for Discrete Multivariate Data. New York: Springer.
Schneider, K. A., & Bavelier, D. (2003). Components of visual prior entry. Cognitive Psychology, 47, 333–366. doi:10.1016/S0010-0285(03)00035-5
Schwarz, W. (2006). On the relationship between the redundant signals effect and temporal order judgments: Parametric data and a new model. Journal of Experimental Psychology: Human Perception and Performance, 32, 558–573. doi:10.1037/0096-1523.32.3.558
Sternberg, S., & Knoll, R. L. (1973). The perception of temporal order: Fundamental issues and a general model. In S. Kornblum (Ed.), Attention and Performance IV (pp. 629–685). New York: Academic Press.
van Eijk, R. L. J., Kohlrausch, A., Juola, J. F., & van de Par, S. (2008). Audiovisual synchrony and temporal order judgments: Effects of experimental method and stimulus type. Perception & Psychophysics, 70, 955–968. doi:10.3758/PP.70.6.955
van Eijk, R. L. J., Kohlrausch, A., Juola, J. F., & van de Par, S. (2010). Temporal order judgment criteria are affected by synchrony judgment sensitivity. Attention, Perception, & Psychophysics, 72, 2227–2235. doi:10.3758/APP.72.8.2227
Vroomen, J., & Stekelenburg, J. J. (2011). Perception of intersensory synchrony in audiovisual speech: Not that special. Cognition, 118, 75–83. doi:10.1016/j.cognition.2010.10.002
Yamamoto, S., & Kitazawa, S. (2001). Reversal of subjective temporal order due to arm crossing. Nature Neuroscience, 4, 759–765. doi:10.1038/89559
Yarrow, K., Jahn, N., Durant, S., & Arnold, D. H. (2011). Shifts of criteria or neural timing? The assumptions underlying timing perception studies. Consciousness and Cognition, 20, 1518–1531. doi:10.1016/j.concog.2011.07.003
Yates, M. J., & Nicholls, M. E. R. (2011). Somatosensory prior entry assessed with temporal order judgments and simultaneity judgments. Attention, Perception, & Psychophysics, 73, 1586–1603. doi:10.3758/s13414-011-0117-7
Zampini, M., Guest, S., Shore, D. I., & Spence, C. (2005). Audio–visual simultaneity judgments. Perception & Psychophysics, 67, 531–544. doi:10.3758/BF03193329
Zampini, M., Shore, D. I., & Spence, C. (2003). Audiovisual temporal order judgments. Experimental Brain Research, 152, 198–210. doi:10.1007/s00221-003-1536-z
Acknowledgments
This research was supported by grant PSI2009-08800 from Ministerio de Ciencia e Innovación (Spain). Correspondence concerning this article should be sent to Rocío Alcalá-Quintana, Departamento de Metodología, Facultad de Psicología, Universidad Complutense, Campus de Somosaguas, 28223 Madrid, Spain (e-mail: ralcala@psi.ucm.es).
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
ESM 1
(ZIP 229 kb)
Appendices
Appendix 1
An often overlooked problem of routines that fit psychometric functions is that they may provide unrealistically low or high parameter estimates (when bounds are not imposed) or boundary estimates (when bounds are imposed). Typically, this is the result of a blind numerical search for parameter values that maximize the likelihood, however minimal the improvement is for unrealistic or boundary values. This outcome is often the result of noninformative data for estimation of that particular parameter (see García-Pérez & Alcalá-Quintana, 2005). The resultant problem was described in detail in Appendix 3 of García-Pérez and Alcalá-Quintana (2012a) for the case of SJ and TOJ data, where boundary estimates were regarded as missing values. These routines implement an alternative solution that is described in this appendix.
Consider the empirical data in Fig. 14a, which also shows psychometric functions fitted jointly to data from the three tasks using the same set of 16 multidimensional starting points defined in sample code earlier in this article. This solution was obtained “blindly” and, thus, rendered a boundary estimate for parameter λ r, as seen in the parameter list on the right of the figure. Recall that this value implies that the standard deviation of visual arrival latencies is estimated to be an unrealistic 3 ms and it is responsible for the sharp corners that psychometric functions in all panels of Fig. 14a show at SOAs of about 0 and 200 ms. Clearly, data are not conclusive about how sharp these corners are, because the range of SOAs turned out to be too broad, including too many uninformative levels (i.e., SOAs at or below −200 ms and SOAs at or above 300 ms) and failing to sample with sufficient density the more informative range between −200 and 300 ms. Naturally, the inadequacy of the chosen range of stimulus levels for this particular observer could not have been anticipated, as is the case in any empirical study.
Fit of error model 1 jointly to data from SJ2, SJ3, and TOJ tasks. The data come from observer #1 in the bouncing-ball experiment of van Eijk et al. (2008). a Fit obtained by taking the best solution across 16 starting values. Parameter estimates (excluding error and bias parameters) are shown on the right, revealing a boundary estimate of λ r that is responsible for the sharp corners of the fitted curves. The negative log-likelihood of the final solution is 665.47. b Improved fit obtained by taking the best solution across starting values not rendering boundary estimates. The negative log-likelihood of this alternative solution is 667.62 (only 0.3% larger than that of the absolute best solution), and it gives a similar account of the data with a more tenable estimate of λr and with no major change in the estimated values of the remaining parameters
Setting  and
and  in the call to
in the call to  renders the following console output:
renders the following console output:

where lines set in bold identify starting points yielding the (absolute) optimal solution illustrated in Fig. 14a, all of which happen to include the same boundary estimate for λ r. In contrast, the remaining starting points rendered a solution that is only meaninglessly worse by the likelihood criterion (the negative log-likelihood is 667 instead of 665, a measly 0.3% higher) and produced the fitted curves and parameter estimates shown in Fig. 14b. The fit looks equally good by eye (and also according to the X 2 and G 2 statistics), but the estimate of λr is now a more realistic 21.27 ms, while the estimates of the remaining parameters are only minimally affected (recall that all these parameters have units of milliseconds). Naturally, performance measures (PSSs, JNDs, synchrony ranges, etc.) are not affected either, because they are insensitive to the sharpness of the corners of the fitted functions.
All fitting routines implement the approach that renders Fig. 14b in this example, namely:
-
1.
seek the absolute best solution across the set of multidimensional starting points;
-
2.
if this solution does not include estimates of λ t or λ r at the upper bound defined in
 , return this solution;
, return this solution; -
3.
otherwise, seek the best alternative solution not involving boundary estimates and
-
3.1.
if any such solution is to be found whose negative log-likelihood does not exceed by 0.5% that of the absolute best solution, return this alternative solution;
-
3.2.
otherwise (i.e., if all solutions include boundary estimates or if the best solution not including them reflects a meaningfully poorer fit by the +0.5% criterion), return the absolute best solution with a warning message.
-
3.1.
Note that this corrective action takes place only when estimates of λ
t or λ
r lie at the upper bound defined in  . The occurrence of estimates at the lower bound also issues a message to the console, but typically this reflects only that the lower bound was set too high by the user. A rerun after reducing the lower bound sufficiently always yields satisfactory results.
. The occurrence of estimates at the lower bound also issues a message to the console, but typically this reflects only that the lower bound was set too high by the user. A rerun after reducing the lower bound sufficiently always yields satisfactory results.
The strategy just discussed cannot prevent near-boundary estimates that may seem equally inappropriate. For instance, estimates of λ
t or λ
r might turn out to be, for example, 0.32 when the upper bound in  is set at 1/3 (as in our examples). This could indeed be an outcome of the strategy just described, when boundary estimates at 1/3 are discarded but replaced with a near-boundary estimate that is equally untenable. A sensible strategy to handle these cases is a rerun in which the upper bound is set higher (say, at 1/4) so that the previous boundary or near-boundary solutions are no longer arrived at and a potential boundary solution now at 1/4 can be replaced with a more tenable alternative across the set of starting values. This process may require some iteration (i.e., a second rerun now using an upper bound at 1/5, and so on), but recall that the success of this approach ultimately depends only on how informative the data are.
is set at 1/3 (as in our examples). This could indeed be an outcome of the strategy just described, when boundary estimates at 1/3 are discarded but replaced with a near-boundary estimate that is equally untenable. A sensible strategy to handle these cases is a rerun in which the upper bound is set higher (say, at 1/4) so that the previous boundary or near-boundary solutions are no longer arrived at and a potential boundary solution now at 1/4 can be replaced with a more tenable alternative across the set of starting values. This process may require some iteration (i.e., a second rerun now using an upper bound at 1/5, and so on), but recall that the success of this approach ultimately depends only on how informative the data are.
Appendix 2
A thorough comparative study of sampling plans for efficient and accurate estimation of the parameters of the independent-channels model adopted here falls in the realm of analyses of experimental designs (see, e.g., García-Pérez, 2000, 2001; García-Pérez & Alcalá-Quintana, 2005). Such a study is beyond the scope of this article, whose only goal is to describe routines that carry out the estimation for given data. Nevertheless, this appendix illustrates the outcomes of reasonably realistic sampling plans with trials placed at informative SOAs. Informative SOAs are those contained within the interval [Δt inf , Δt sup], where Δt inf and Δt sup are the SOAs satisfying ΨS(Δt inf) = ΨS(Δt sup) = .09 in Equation 3b, although moving this criterion level down to .05 does not have any major implication. In simulations such as those reported here, these SOA boundaries are easily computed from the true parameters of the simulees; in empirical studies, they can be identified using adaptive methods during the first 30–40 trials of the session with each observer, which will help set the MOCS levels subsequently used.
Because error rates are generally negligible for most observers, except occasionally and typically for only one of these error parameters (see García-Pérez & Alcalá-Quintana, 2012a), these simulations assumed error model 0 without loss of generality. One thousand sets of parameter values were independently drawn from uniform distributions on [1/80, 1/20] for λ t and λ r, on [20, 150] for δ, on [−80, 80] for τ, and on [0.1, 0.9] for ξ. These were used to simulate responses to SJ2, SJ3, and TOJ tasks under various combinations of number of SOAs and number of trials per SOA, all of which render an overall number of around 350 trials: 7 × 50 (#SOAs × #trials per SOA), 8 × 45, 9 × 40, 10 × 35, 11 × 30, 14 × 25, and 17 × 20. Error model 0 was then fitted separately to data from each task and errors of estimation (the difference between estimated value and true value) were computed for each parameter.
Figure 15 shows results for the case of 11 SOAs and 30 trials per SOA, but results for other combinations were indistinguishable. The accuracy with which the four major parameters (λ
t, λ
r, δ, and τ; see Fig. 15a) are estimated seems adequate under SJ3 tasks (center column) and, to a slightly lesser extent, under SJ2 tasks (left column). Certainly, larger overall numbers of trials are needed to estimate these parameters from TOJ data (right column), in line with results reported elsewhere (García-Pérez & Alcalá-Quintana, 2012a) and providing further evidence of the inadequacy of the TOJ task. Figure 15b shows the distribution of errors of estimation affecting PSSs, under two approaches: in the top row, for the PSS estimates that arise from model parameter estimates through the  routine in our package; in the bottom row, for the PSS estimates that arise under the conventional practice of fitting Gaussian functions to S data from SJ2 or SJ3 tasks, or fitting logistic functions to TOJ data. Quite clearly, PSS estimates are less accurate from the conventional fit, and despite the apparent imprecision with which model parameters are estimated in the TOJ task. The inferiority of PSS estimates obtained by fitting Gaussian or logistic functions to these data was apparent under all the remaining combinations of numbers of SOAs and numbers of trials per SOA in these simulations. And the inferiority of JND estimates from conventional fits was also obvious and particularly large in SJ2 and SJ3 tasks, because S data hardly ever describe the symmetric and sharply peaked shape of a Gaussian function.
routine in our package; in the bottom row, for the PSS estimates that arise under the conventional practice of fitting Gaussian functions to S data from SJ2 or SJ3 tasks, or fitting logistic functions to TOJ data. Quite clearly, PSS estimates are less accurate from the conventional fit, and despite the apparent imprecision with which model parameters are estimated in the TOJ task. The inferiority of PSS estimates obtained by fitting Gaussian or logistic functions to these data was apparent under all the remaining combinations of numbers of SOAs and numbers of trials per SOA in these simulations. And the inferiority of JND estimates from conventional fits was also obvious and particularly large in SJ2 and SJ3 tasks, because S data hardly ever describe the symmetric and sharply peaked shape of a Gaussian function.
Distribution of errors of estimation (difference between estimated value and true value) for data from each task (columns) always involving 11 SOAs and 30 trials per SOA. Each histogram includes 1,000 estimates. a Results concerning the four major model parameters (see labels on the right). b Results concerning PSSs, computed either from estimates of model parameters (top row), or from Gaussian functions fitted to SJ2 and SJ3 data or logistic functions fitted to TOJ data (bottom row)
Rights and permissions
About this article
Cite this article
Alcalá-Quintana, R., García-Pérez, M.A. Fitting model-based psychometric functions to simultaneity and temporal-order judgment data: MATLAB and R routines. Behav Res 45, 972–998 (2013). https://doi.org/10.3758/s13428-013-0325-2
Published:
Issue Date:
DOI: https://doi.org/10.3758/s13428-013-0325-2



 3 × N
SJ2 matrix with data from the SJ2 task arranged as in Fig.
3 × N
SJ2 matrix with data from the SJ2 task arranged as in Fig.  4 × N
SJ3 matrix with data from the SJ3 task arranged as in Fig.
4 × N
SJ3 matrix with data from the SJ3 task arranged as in Fig.  3 × N
TOJ matrix with data from the TOJ task arranged as in Fig.
3 × N
TOJ matrix with data from the TOJ task arranged as in Fig.  A 1 × 2 row vector stating the lower and upper bounds for both λr and λt (positive reals).
A 1 × 2 row vector stating the lower and upper bounds for both λr and λt (positive reals). A 1 × 2 row vector stating the lower and upper bounds for τ (reals). The suggested option for general use is
A 1 × 2 row vector stating the lower and upper bounds for τ (reals). The suggested option for general use is 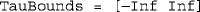 , to be changed only in a re-rerun with the same data to prevent untenably large estimates (in absolute value) that will, nevertheless, rarely be obtained even when the data are scarce.
, to be changed only in a re-rerun with the same data to prevent untenably large estimates (in absolute value) that will, nevertheless, rarely be obtained even when the data are scarce. A 1 × 2 row vector stating the lower and upper bounds for δ (positive reals). The suggested option for general use is
A 1 × 2 row vector stating the lower and upper bounds for δ (positive reals). The suggested option for general use is  , to be changed only in a re-rerun with the same data to prevent untenably large estimates that will, nevertheless, rarely be obtained even when the data are scarce.
, to be changed only in a re-rerun with the same data to prevent untenably large estimates that will, nevertheless, rarely be obtained even when the data are scarce. Starting value(s) for parameter λt. This argument must be a positive real and can be a scalar (to set a single starting value) or a row vector (to set several of them).
Starting value(s) for parameter λt. This argument must be a positive real and can be a scalar (to set a single starting value) or a row vector (to set several of them). Starting value(s) for parameter λr (positive real). Can be a scalar or a row vector.
Starting value(s) for parameter λr (positive real). Can be a scalar or a row vector. Starting value(s) for parameter τ (real). Can be a scalar or a row vector.
Starting value(s) for parameter τ (real). Can be a scalar or a row vector. Starting value(s) for parameter δ (positive real). Can be a scalar or a row vector.
Starting value(s) for parameter δ (positive real). Can be a scalar or a row vector. Starting value(s) for all response error parameters (εTF, εS, and εRF for each task), in the interval [0, 1]. Can be a scalar or a row vector.
Starting value(s) for all response error parameters (εTF, εS, and εRF for each task), in the interval [0, 1]. Can be a scalar or a row vector. Starting value(s) for parameter ξ and for all κs, in the interval [0, 1]. Can be a scalar or a row vector.
Starting value(s) for parameter ξ and for all κs, in the interval [0, 1]. Can be a scalar or a row vector.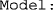 Choice of model, according to codes given in Table
Choice of model, according to codes given in Table 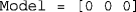 and
and 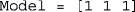 —or, in R,
—or, in R,  and
and 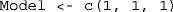 — can be simplified to a single scalar (i.e.,
— can be simplified to a single scalar (i.e., 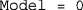 or
or 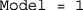 ). For the routine to return the best-fitting model by the BIC, set
). For the routine to return the best-fitting model by the BIC, set 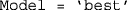 (case insensitive).
(case insensitive). A logical scalar. If true, a plot showing data and fitted functions is created; otherwise, no plot is created.
A logical scalar. If true, a plot showing data and fitted functions is created; otherwise, no plot is created. A logical scalar. If true, messages are issued to the console as the routine progresses. If a single model was selected, a message is issued for each of the multidimensional starting points used (see an example in the
A logical scalar. If true, messages are issued to the console as the routine progresses. If a single model was selected, a message is issued for each of the multidimensional starting points used (see an example in the 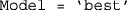 , a message is issued for each candidate model, omitting messages for each of the multidimensional starting points used. Setting true this argument also issues a message if the estimates of λr or λt lie at one of the bounds defined in
, a message is issued for each candidate model, omitting messages for each of the multidimensional starting points used. Setting true this argument also issues a message if the estimates of λr or λt lie at one of the bounds defined in  .
.



 The number n of bootstrap samples to be generated (an integer scalar greater than 1).
The number n of bootstrap samples to be generated (an integer scalar greater than 1). The confidence coefficient for CIs (a real scalar between 80 and 99.9).
The confidence coefficient for CIs (a real scalar between 80 and 99.9). A logical scalar. When true, random number generators are initialized to a fixed seed, thus producing the same results whenever the same input arguments are given; when false, generators are initialized to a random seed, thus producing results subject to sampling error across repeated calls with the same input arguments.
A logical scalar. When true, random number generators are initialized to a fixed seed, thus producing the same results whenever the same input arguments are given; when false, generators are initialized to a random seed, thus producing results subject to sampling error across repeated calls with the same input arguments.
 Test-first simultaneity boundary (the 50% point on the left side of the psychometric function for S judgments).
Test-first simultaneity boundary (the 50% point on the left side of the psychometric function for S judgments). Reference-first simultaneity boundary (the 50% point on the right side of the psychometric function for S judgments).
Reference-first simultaneity boundary (the 50% point on the right side of the psychometric function for S judgments).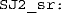 Simultaneity range (the distance between the two boundaries just described).
Simultaneity range (the distance between the two boundaries just described). The midpoint between the two boundaries (one of the definitions of the PSS).
The midpoint between the two boundaries (one of the definitions of the PSS). The peak of the psychometric function for S judgments (another definition of the PSS).
The peak of the psychometric function for S judgments (another definition of the PSS).
 Test-first simultaneity boundary (the crossing point of the psychometric functions for TF and S judgments).
Test-first simultaneity boundary (the crossing point of the psychometric functions for TF and S judgments). Reference-first simultaneity boundary (the crossing point of the psychometric functions for S and RF judgments).
Reference-first simultaneity boundary (the crossing point of the psychometric functions for S and RF judgments). Simultaneity range (the distance between the two boundaries just described).
Simultaneity range (the distance between the two boundaries just described). The midpoint between the two boundaries (one of the definitions of the PSS).
The midpoint between the two boundaries (one of the definitions of the PSS). The peak of the psychometric function for S judgments (another definition of the PSS).
The peak of the psychometric function for S judgments (another definition of the PSS).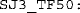 The 50% point on the psychometric function for TF judgments.
The 50% point on the psychometric function for TF judgments. The 50% point on the psychometric function for RF judgments.
The 50% point on the psychometric function for RF judgments.
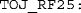 The 25% point on the psychometric function for RF responses.
The 25% point on the psychometric function for RF responses. The 50% point on the psychometric function for RF responses (the PSS).
The 50% point on the psychometric function for RF responses (the PSS). The 75% point on the psychometric function for RF responses.
The 75% point on the psychometric function for RF responses. The distance between the 25% and the 75% points.
The distance between the 25% and the 75% points.
 The 50% point (i.e., the latent PSS) on the psychometric function for latent RF judgments if the observer had infinite resolution (i.e., as if δ = 0, even if the corresponding input parameter was not set to 0).
The 50% point (i.e., the latent PSS) on the psychometric function for latent RF judgments if the observer had infinite resolution (i.e., as if δ = 0, even if the corresponding input parameter was not set to 0). The 15.87% point on the latent psychometric function.
The 15.87% point on the latent psychometric function.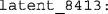 The 84.13% point on the latent psychometric function.
The 84.13% point on the latent psychometric function. The distance between the 15.87% and the 84.13% points (a measure of sensitivity). Half this value is what the standard deviation would be if the psychometric function were a cumulative Gaussian.
The distance between the 15.87% and the 84.13% points (a measure of sensitivity). Half this value is what the standard deviation would be if the psychometric function were a cumulative Gaussian.



 is called with the option
is called with the option  as the choice of algorithm. In MATLAB, the function
as the choice of algorithm. In MATLAB, the function  is part of the Optimization Toolbox, and we chose to use it because the function
is part of the Optimization Toolbox, and we chose to use it because the function  available in the basic MATLAB package uses only the Nelder–Mead algorithm, which proved to be nondependable in this particular application. The function
available in the basic MATLAB package uses only the Nelder–Mead algorithm, which proved to be nondependable in this particular application. The function  has changed over releases, mostly in what regards the default and available optimization algorithms. For this reason, the routines check the running version and set options for
has changed over releases, mostly in what regards the default and available optimization algorithms. For this reason, the routines check the running version and set options for  as follows. For releases dated 2007 or earlier, the option
as follows. For releases dated 2007 or earlier, the option  is set to
is set to  ; for releases dated 2008 or 2009, the new option
; for releases dated 2008 or 2009, the new option  is set to
is set to  ; for releases dated 2010 or later, the option
; for releases dated 2010 or later, the option  is set to the new value
is set to the new value  .
. in their installation.
in their installation. because then this field will indicate which model turned out to be the best.
because then this field will indicate which model turned out to be the best.
 , return this solution;
, return this solution;