Abstract
We introduce MPTinR, a software package developed for the analysis of multinomial processing tree (MPT) models. MPT models represent a prominent class of cognitive measurement models for categorical data with applications in a wide variety of fields. MPTinR is the first software for the analysis of MPT models in the statistical programming language R, providing a modeling framework that is more flexible than standalone software packages. MPTinR also introduces important features such as (1) the ability to calculate the Fisher information approximation measure of model complexity for MPT models, (2) the ability to fit models for categorical data outside the MPT model class, such as signal detection models, (3) a function for model selection across a set of nested and nonnested candidate models (using several model selection indices), and (4) multicore fitting. MPTinR is available from the Comprehensive R Archive Network at http://cran.r-project.org/web/packages/MPTinR/.
Similar content being viewed by others
Multinomial processing tree (MPT) models represent a prominent class of cognitive measurement models for categorical data (Hu & Batchelder, 1994; Purdy & Batchelder, 2009; Riefer & Batchelder, 1988). They describe the observed response frequencies from a finite set of response categories (i.e., responses following a multinomial distribution) with a finite number of latent states. Each latent state is reached by particular combinations of cognitive processes—processes that are assumed to take place in an all-or-nothing fashion (e.g., a previously seen item is remembered as having been seen or not). The probability of a latent state being reached depends on the probabilities that the different cognitive processes associated to it will successfully take place. The latent states usually follow each other in a serial order that can be displayed in a tree-like structure (see Fig. 1; this model is described in more detail below).
A MPT model (2HTM) for recognition memory. On the left side are the two different item types—old and new items, respectively—each represented by one tree. On the right side are the observed responses “Old” and “New.” In between are the assumed latent states with the probabilities leading to these states. Each tree is traversed from left to right. D o = detect an old item as old, D n = detect a new item as new, g = guess an item as old
MPT models exist in a wide range of fields, such as memory, reasoning, perception, categorization, and attitude measurement (for reviews, see Batchelder & Riefer, 1999; Erdfelder, Auer, Hilbig, Aßfalg, Moshagen, & Nadarevic, 2009), where they provide a superior data analysis strategy, as compared with the usually employed ad hoc models (e.g., ANOVA). MPT models allow the decomposition of observed responses into latent cognitive processes with a psychological interpretation, whereas ad hoc models permit only the testing of hypotheses concerning the observed data, the model parameters do not have a psychological interpretation, and the models do not provide any insight into the underlying cognitive processes. In this article, we present a package for the analysis of MPT models for the statistical programming language R (R Development Core Team, 2012b), called MPTinR, that offers several advantages over comparable software (see Moshagen, 2010, for a comparison of software for the analysis of MPTs).
The remainder of this article is organized as follows. In the next section, we will introduce a particular MPT model as an example. In the section thereafter, we will provide a general overview of model representation, parameter estimation, and statistical inference in the MPT model class. This overview is by no means exhaustive, but it gives several references that provide in-depth analysis. In the section thereafter, we introduce MPTinR and its functionalities and provide an example session introducing the most important functions for model fitting, model selection, and simulation. Furthermore, an overview of all functions in MPTinR is given, followed by a brief comparison of MPTinR with other software for analyzing MPT models. Finally, the Appendix contains a description of the algorithms used by MPTinR.
An example MPT: The two-high threshold model of recognition memory
Consider the model depicted in Fig. 1, which describes the responses produced in a simple recognition memory experiment consisting of two phases: a learning phase in which participants study a list of items (e.g., words) and, subsequently, a test phase in which a second list is presented and participants have to indicate which items were previously studied (old items) and which were not (new items) by responding “Old” or “New,” respectively.
This particular MPT model for the recognition task—the two-high threshold model (2HTM; Snodgrass & Corwin, 1988)—has been chosen because of its simplicity. It consists of two trees, with the item type associated with each tree (old and new items) specified at the tree’s root. Response categories are specified at the leaves of the trees. Cognitive processes are specified in a sequential manner by the tree nodes, and their outcomes (successful occurrence or not) are represented by the branches that emerge from these nodes. The probability of each cognitive process successfully occurring is defined by a parameter.
Let us first consider the old-item tree. When presented with an old item at test, a state of successful remembering is reached with probability D o (= detect old), and the “Old” response is then invariably given. If the item is not remembered [with probability (1 − D o )], the item is guessed to be “Old” with probability g (= guessing), or to be “New” with probability (1 − g). Regarding the new-item tree, items can be detected as nonstudied with probability D n (= detect new), leading to the items’ rejection (“New” response). If the new item is not detected [with probability (1 − D n )], it is guessed to be “Old” or “New” with probabilities g and (1 − g), respectively. The predicted response probabilities for each observable response category can be represented by a set of equations:
These equations are constructed by concatenating all branches leading to the same observable response category (e.g., “Old”) within one tree. For example, the first line concatenates all branches leading to an “Old” response in the old-item tree. As was stated above, for old items, the response “Old” is given either when an item is successfully remembered as being old (D o ) or, if it is nor remembered as being old, by guessing [\( + \left( {1 - {D_o}} \right) \times g \)]. Note that the responses associated to the equations above provide only two degrees of freedom, while the model equations assume three free parameters (D o , D n , and g), which means that the model is, in the present form, nonidentifiable (see Bamber & van Santen, 1985). This issue will be discussed in greater detail below.
The model presented above describes observed responses in terms of a set of unobservable latent cognitive processes—namely, a mixture of (1) memory retrieval (D o ), (2) distractor detection (D n ), and (3) guessing (g). Whereas the memory parameters are specific for the item types (i.e., D o is only part of the old item tree, and D n is only part of the new item tree), the same guessing parameter is present in both trees. This means that it is assumed that guessing (or response bias) is identical whether or not an item is old or new, reflecting that the status of each item (old or new) is completely unknown to the participants when guessing. Note that this psychological interpretation of the parameters requires validation studies. In these studies, it needs to be shown that certain experimental manipulations expected to selectively affect certain psychological processes are reflected in the resulting model parameters, with changes being reliably found only in the parameters representing those same processes (see Snodgrass & Corwin, 1988, for validation studies of 2HTM parameters).
The contribution of each of the assumed cognitive processes can be assessed by finding the parameter values (numerically or analytically) that produce the minimal discrepancies between predicted and observed responses. The discrepancies between predicted and observed responses can be quantified by a divergence statistic (Read & Cressie, 1988). As we discuss in more detail below, discrepancies between models and data can be used to evaluate the overall adequacy of the model and to test focused hypotheses on parameters (e.g., parameters have the same values across conditions).
Representation, estimation, and inference in MPT models: A brief overview
Model specification and parameter estimation
Following the usual formalization (Hu & Batchelder, 1994) of MPT models, let \( \varTheta = \left\{ {{\theta_1},\ldots, {\theta_S}} \right\} \), with \( 0 \leqslant {\theta_s} \leqslant 1 \), s = 1, …, S denote the vector of S model parameters representing the different cognitive processes. For tree k, the probability of a branch i leading to response category j given \( \varTheta \) corresponds to
where a s,i,j,k and b s,i,j,k represent the number of times each parameter θ s and its complement (1 − θ s ) are respectively represented at each branch i leading to category j of tree k, and c i,j,k represents the product of constants on the tree links, if the latter are present. The probability of category j, k given \( \varTheta \) corresponds to \( {p_{{j,k}}}\left( \varTheta \right) = \sum\nolimits_{{i = 1}}^{{{I_{{j,k}}}}} {{p_{{i,j,k}}}\left( \varTheta \right)} \) (i.e., the sum of all branches ending in one response category per tree), with \( \sum\nolimits_{{j = 1}}^{{{J_k}}} {{p_{{j,k}}}\left( \varTheta \right) = 1} \) (i.e., the sum of all probabilities per tree is 1).
Let n be a vector of observed category frequencies, with n j,k denoting the frequency of response category j in tree k, with \( {N_k} = \sum\nolimits_{{j = 1}}^{{{J_k}}} {{n_{{j,k}}}} \) and \( N = \sum\nolimits_{{k = 1}}^K {{N_k}} \). The likelihood function of n given model parameter vector \( \varTheta \) is
The parameter values that best describe the observed responses correspond to the ones that maximize the likelihood function in Equation 6. These maximum-likelihood parameter estimates (denoted by \( \widehat{\varTheta } \)) can sometimes be obtained analytically (e.g., Stahl, & Klauer, 2008), but in the vast majority of cases, they can be found only by means of iterative methods such as the EM algorithm (see Hu & Batchelder, 1994). Regarding the variability of the maximum-likelihood parameter estimates, confidence intervals can be obtained by means of the Fisher information matrix (the matrix of second-order partial derivatives of the likelihood function with respect to \( \varTheta \); Riefer & Batchelder, 1988) or via bootstrap simulation (Efron & Tibshirani, 1994).
The search for the parameters that best describe the data (maximize the likelihood function) requires that the model is identifiable. Model identifiability concerns the property that a set of predicted response probabilities can be obtained only by a single set of parameter values. Let \( \varTheta \) and \( \varTheta \prime \) be model parameter vectors, with \( p\left( \varTheta \right) \) and \( p\left( {\varTheta \prime } \right) \) as their respective predicted response probabilities. A model is globally identifiable if \( \varTheta \ne \varTheta \prime \) implies \( p\left( \varTheta \right) \ne p\left( {\varTheta \prime } \right) \) across the entire parameter space and is locally identifiable if it holds in the region of parameter space where \( \widehat{\varTheta } \) lies (Schmittmann, Dolan, Raijmakers, & Batchelder, 2010). An important aspect is that the degrees of freedom provided by a data set provide the upper bound for the number of potentially identifiable free parameters in an model—that is, \( S \leqslant \sum\nolimits_{{k = 1}}^K {\left( {{J_k} - 1} \right)} \). Local identifiability is sufficient for most purposes, and it can be shown to hold by checking that the Fisher information matrix for \( \widehat{\varTheta } \) has rank equal to the number of free parameters (the rank of the Fisher information matrix is part of the standard output produced by MPTinR). For a detailed discussion on model identifiability in the MPT model class, see Schmittman et al.
Null-hypothesis testing
The discrepancies between predicted and observed response frequencies when taking the maximum-likelihood parameter estimates (\( \widehat{\varTheta } \)) are usually summarized by the G 2 statistic:
The smaller G 2, the smaller the discrepancies.Footnote 1 An important aspect of the G 2 statistic is that it follows a chi-square distribution with degrees of freedom equal to the number of independent response categories minus the number of free parameters \( \left( {\left[ {\sum\nolimits_{{k = 1}}^K \,({J_k} - 1)} \right] - S} \right) \). This means that the quality of the account provided by the model can be assessed through null-hypothesis testing. Parameter equality restrictions (e.g., θ 1 = θ 2 or θ 1 = 0.5) can also be tested by means of null-hypothesis testing. The difference in G 2 between the unrestricted and restricted models also follows a chi-square distribution with degrees of freedom equal to the difference in free parameters between the two models (Riefer & Batchelder, 1988). It should be noted that parameter inequality restrictions (e.g., \( {\theta_1} \leqslant {\theta_2} \); see Knapp & Batchelder, 2004) can also be tested, but the difference in G 2 no longer follows a chi-square distribution but a particular mixture of chi-square distributions that, in many cases, needs to be determined via simulation (Silvapulle & Sen, 2005; for an example, see Kellen & Klauer, 2011).
Model selection
It is important to note that G 2 is a measure that only summarizes the models’ goodness of fit and that can only be used to test between nested models (when the restricted model is a special case of the unrestricted model). Furthermore, it ignores possible flexibility differences between the models—that is, differences in their inherent ability to fit data in general. The more flexible a model is, the better it will fit any data pattern, regardless of the appropriateness of the model. The best model is not necessarily the one that better fits the data, since it is also important that a model’s range of predictions closely follows the observations made and that it can produce accurate predictions regarding future observations (Roberts & Pashler, 2000). Model selection analyses attempt to find the model that strikes the best balance between goodness of fit and model flexibility (for discussions on different model selection approaches, see Myung, Forster, & Browne, 2000; Wagenmakers & Waldorp, 2006), which makes G 2 an unsuitable measure for the comparison of nonnested models. In order to compare both nested and nonnested models in a single framework, as well as to account for potential differences in model flexibility, measures such as the Akaike information criterion (AIC; Akaike, 1974) and the Bayesian information criterion (BIC; Schwarz, 1978) are used:Footnote 2
AIC and BIC correct models’ fit results by introducing a punishment factor (the second term in the formulas) that penalizes them for their flexibility (S is the number of parameters). The lower the AIC/BIC, the better the account. For the case of AIC and BIC, the number of free parameters is used as a proxy for model flexibility, a solution that is convenient to use but that ignores differences in the model’s functional form and is rendered useless when used to compare models that have the same number of parameters (Klauer & Kellen, 2011). For example, consider the structurally identical models A and B with two parameters θ 1 and θ 2, with the sole difference between both models that, for model B, the restriction \( {\theta_1} \leqslant {\theta_2} \) holds. According to AIC and BIC, the models are equally flexible despite the fact that the inequality restriction halves model B’s parameter space and, therefore, its flexibility.
A measure that provides a more precise quantification of model flexibility is the Fisher information approximation (FIA), a measure that stems from the minimum description length framework (for an introduction, see Grünwald, 2007):
where \( I\left( \varTheta \right) \) is the Fisher information matrix for sample size 1 (for details, see Su, Myung, & Pitt, 2005). The third additive term of Equation 10 is the penalty factor that accounts for the functional form of the model, providing a more accurate depiction of a model’s flexibility. Unlike AIC and BIC, FIA can account for flexibility differences in models that have the same number of parameters. Despite its advantages, FIA is a measure whose computation is far from trivial, given the integration of the determinant of the Fisher information matrix across a multidimensional parameter space. Due to the recent efforts of Wu, Myung, and Batchelder (2010a, 2010b), the computation of FIA for the MPT model class has become more accessible.
Context-free language for MPTs
Also of interest is the context-free language for the MPT model class developed by Purdy and Batchelder (2009), called \( {{\mathrm{L}}_{\mathrm{BMPT}}} \). In \( {{\mathrm{L}}_{\mathrm{BMPT}}} \), each MPT model is represented by a string, called a word, consisting only of symbols representing parameters (θ) or categories (C). The word in \( {{\mathrm{L}}_{\mathrm{BMPT}}} \) representing each tree is created by recursively performing the following operations:
-
1.
visit the root
-
2.
traverse the upper subtree
-
3.
traverse the lower subtree.
During these operations, the word is built in the following manner. Whenever a parameter (and not its converse) is encountered, add the parameter to the string. Whenever a response category (i.e., leaf) is reached, add the category to the string. The word is complete when the last response category is reached. The structure for the trees in Fig. 1 in \( {{\mathrm{L}}_{\mathrm{BMPT}}} \) is thus
By assigning indices, one obtains a word in \( {{\mathrm{L}}_{\mathrm{BMPT}}} \) for each tree in Fig. 1:
In order to create a single MPT model of the two trees in Fig. 1, one needs to assume a joining parameter θ join whose branches connect the two trees into a single one. In this case, the values of θ join and (1 − θ join ) would be fixed a priori, since they represent the proportion of times that old and new items occur during test. The resulting full model for the recognition memory experiment in \( {{\mathrm{L}}_{\mathrm{BMPT}}} \) is
The context-free language of Purdy and Batchelder (2009) is extremely useful, since it allows the statement and proof of propositions regarding the MPT model class. One application of this language is in the computation of FIA (Wu et al., 2010a, 2010b).
General overview of MPTinR
MPTinR offers five main advantages over comparable software (cf. Moshagen, 2010). First, MPTinR is fully integrated into the R language, an open-source implementation of the S statistical programming language (Becker, Chambers, & Wilks, 1988), which is becoming the lingua franca of statistics (Muenchen, 2012; Vance, 2009). Besides being free (since it is part of the GNU project; see http://www.gnu.org) and platform independent, R’s major strength is the combination of being extremely powerful (it is a programming language) with the availability of a wide variety of statistical and graphical techniques. Couching MPTinR within this environment lets it benefit from these strengths. For example, data usually need to be preprocessed before fitting an MPT model. In addition to fitting an MPT model, one may want to visualize the parameter estimates, run hypothesis tests on particular parameter restrictions, or perform simulations validating certain aspects of the model, such as the parameter estimates or the identifiability of the model. When MPTinR is used, all of those processes can be done within one single environment without the need to ever move data between programs.
Second, MPTinR was developed with the purpose of being easy to use, improving some of the more cumbersome features of previous programs, such as the ones concerning model representation. MPT models are represented in most programs, such as GPT (Hu & Phillips, 1999), HMMTree (Stahl & Klauer, 2007), or multiTree (Moshagen, 2010), by means of .EQN model files. Model specification in .EQN files needs to follow a certain structure that could lead to errors and diverge from the model equations (e.g., Equations 1–4) that are normally used to represent these models in scientific studies. These requirements can become especially cumbersome when MPT models comprised of trees with numerous branches are handled (e.g., Oberauer, 2006). Furthermore, most programs require parameter restrictions to be specified “by hand” every time the program is used (for an exception, see Moshagen, 2010), or different model files implementing the parameter restrictions have to be created. MPTinR overcomes these inconvenient features: Models are specified in a way that is virtually equivalent to the equations used to represent models (i.e., Equations 1–4), and model restrictions are intuitively specified. Furthermore, model and restrictions can be specified in external files or directly within an R script. In addition, MPTinR automatically detects whether single or multiple data sets are fitted and adjusts the output accordingly. For multiple data sets, the summed results (e.g., summed G 2 values), as well as the results for the aggregate data (i.e., summed response frequencies across data sets), are provided in the output.
Third, MPTinR provides different model selection measures—namely, AIC, BIC, and FIA. As was previously referred to, the computation of FIA is not trivial, and only very recently has it become available for the MPT model class (Wu et al., 2010a, 2010b).
Fourth, MPTinR is able to translate an MPT model into a string representation according to the context-free language developed by Purdy and Batchelder (2009). Given that the manual translation of MPTs can be rather difficult and tedious, the possibility of an automatic translation will likely encourage the use of this context-free language, which has shown great potential in the assessment of model flexibility (see Purdy, 2011).
Fifth, although being specifically designed for MPTs, MPTinR can also be used to fit a wide range of other cognitive models for categorical data—for example, models based on signal detection theory (SDT; Green & Swets, 1966; Macmillan & Creelman, 2005). This essentially makes MPTinR a framework for fitting many types of cognitive models for categorical data and for facilitating their comparison. Since the last point is outside the scope of this article, we refer interested readers to the documentation for the functions  and
and  , which contain detailed examples of how to fit different SDT models (the supplemental material also contains an example on how to fit a signal detection model).
, which contain detailed examples of how to fit different SDT models (the supplemental material also contains an example on how to fit a signal detection model).
Getting started
MPTinR is a package for the R programming language and, therefore, needs to be used within the R environment by using the functions described below. For users familiar with commercial statistic packages such as SPSS, the handling of R may be uncommon, since it does not come with a graphical user interface (but see Valero-Mora & Ledesma, 2012, for an overview, and Rödiger, Friedrichsmeier, Kapat, & Michalke, 2012, for a powerful graphical user interface for R). Instead, all commands have to be entered at the prompt (we will use a  font and the prompt symbol > when presenting R code). MPTinR comes with a manual describing all functions in detail (available also via http://cran.r-project.org/web/packages/MPTinR/MPTinR.pdf) and has a Web site with more information on important features such as model files and restrictions (see http://www.psychologie.uni-freiburg.de/Members/singmann/R/mptinr/modelfile). To obtain the documentation for any function of MPTinR, simply enter the function name at the prompt, preceded by a ? (e.g.,
font and the prompt symbol > when presenting R code). MPTinR comes with a manual describing all functions in detail (available also via http://cran.r-project.org/web/packages/MPTinR/MPTinR.pdf) and has a Web site with more information on important features such as model files and restrictions (see http://www.psychologie.uni-freiburg.de/Members/singmann/R/mptinr/modelfile). To obtain the documentation for any function of MPTinR, simply enter the function name at the prompt, preceded by a ? (e.g.,  to obtain the detailed documentation containing examples for the main function
to obtain the detailed documentation containing examples for the main function  ). The documentation for each function contains a detailed description of its use and the arguments that need to be passed to it. Here, we present only the most relevant arguments of each function.
). The documentation for each function contains a detailed description of its use and the arguments that need to be passed to it. Here, we present only the most relevant arguments of each function.
MPTinR is available via the Comprehensive R Archive Network (CRAN; http://cran.r-project.org/) and can therefore be installed from within any R session with the following command (given an active Internet connection):
Note that you might need an up-to-date version of R to install MPTinR. After successful installation (which needs to be done only once), MPTinR needs to be loaded into the current R session with the following command (this needs to be done each time you start a new R session):
Format of models, restrictions, and data
The basis of all analyses of MPT models in MPTinR is the representation of the model via a model file. Whereas MPTinR can read the well-known .EQN model files (e.g., Hu & Phillips, 1999), it offers an alternative, the  format. To specify a model in the
format. To specify a model in the  format, the model file needs to contain the right-hand sides of the equations defining an MPT model (e.g., Equations 1–4), with the equations for each tree separated by at least a single empty line. In other words, for each tree, all branches ending in the same response category need to be written in a single line concatenated by +. Note that only trees with binary branching can be specified in MPTinR (for an exception, see Hu & Phillips, 1999). The model file for the 2HTM model from Fig. 1 in the
format, the model file needs to contain the right-hand sides of the equations defining an MPT model (e.g., Equations 1–4), with the equations for each tree separated by at least a single empty line. In other words, for each tree, all branches ending in the same response category need to be written in a single line concatenated by +. Note that only trees with binary branching can be specified in MPTinR (for an exception, see Hu & Phillips, 1999). The model file for the 2HTM model from Fig. 1 in the  format could be:
format could be:
As can be seen, MPTinR allows for comments in the model file. Everything to the right of the number sign # will be ignored, and lines containing only a comment count as empty.Footnote 3 Also, additional white space within the equations is ignored. Note that the parameter names used in the model files need to be valid R variable names (for details, type  and
and  at the command prompt).
at the command prompt).
The format of restriction files is similar to the format of model files. Each restriction needs to be specified on one line. Furthermore, the following rules apply: Inequality restrictions need to be placed before equality restrictions and can be specified only by using the smaller than operator  (note that inequality restrictions containing
(note that inequality restrictions containing  actually represent the weak inequality
actually represent the weak inequality  ). If a variable appears not as the rightmost element in a restriction, it can only appear as the rightmost element in any other restriction (in other words, in a set of restrictions, a variable can appear multiple times, but only once not as the rightmost element). In addition to simple equality and inequality restrictions, MPTinR can also deal with restrictions involving more than two parameters. For example, \( Y1 = Y2 = 0.5 \) will set both parameters Y1 and Y2 to 0.5. Similarly, \( W1 < W2 < W3 \) will be correctly interpreted as \( W1 < W2 \) and \( W2 < W3 \). A valid restrictions file (for a fictitious MPT model) could be:
). If a variable appears not as the rightmost element in a restriction, it can only appear as the rightmost element in any other restriction (in other words, in a set of restrictions, a variable can appear multiple times, but only once not as the rightmost element). In addition to simple equality and inequality restrictions, MPTinR can also deal with restrictions involving more than two parameters. For example, \( Y1 = Y2 = 0.5 \) will set both parameters Y1 and Y2 to 0.5. Similarly, \( W1 < W2 < W3 \) will be correctly interpreted as \( W1 < W2 \) and \( W2 < W3 \). A valid restrictions file (for a fictitious MPT model) could be:

Note that it is also possible to specify model and restriction within an R script (as compared with in an external file), using, for example, the  function included in the base R package. Restrictions can also be specified within a script as a
function included in the base R package. Restrictions can also be specified within a script as a  of strings. See the supplemental material and the documentations for functions
of strings. See the supplemental material and the documentations for functions  and
and  for examples.
for examples.
MPTinR contains the function  that may help in writing model and restriction files. It has the format
that may help in writing model and restriction files. It has the format 
 and will return a list with the following information: a logical value indicating whether or not the probabilities on each tree sum to one, the number of trees and the number of response categories the model has, the number of independent response categories the model provides, and the name and number of the parameters in the tree. The only mandatory argument is
and will return a list with the following information: a logical value indicating whether or not the probabilities on each tree sum to one, the number of trees and the number of response categories the model has, the number of independent response categories the model provides, and the name and number of the parameters in the tree. The only mandatory argument is  , which needs to be a character string specifying the location and name of the model file.Footnote 4 An optional argument is
, which needs to be a character string specifying the location and name of the model file.Footnote 4 An optional argument is  , which specifies the location and name of the restrictions file.
, which specifies the location and name of the restrictions file.
For example, calling  on the 2HTM model saved in a file
on the 2HTM model saved in a file  in the current working directory of R will return an output indicating that the probabilities in each tree sum to one (if not, the function will pinpoint the misspecified trees), that the number of trees in the model is two, the number of response categories is four, the number of independent response categories is two, and the three parameters are D
n
, D
o
, and g:
in the current working directory of R will return an output indicating that the probabilities in each tree sum to one (if not, the function will pinpoint the misspecified trees), that the number of trees in the model is two, the number of response categories is four, the number of independent response categories is two, and the three parameters are D
n
, D
o
, and g:

The data on which an MPT model will be fitted needs to be passed as a numeric data object, as a  , or
, or  . The mapping of data to response category is done via position. The ordinal position (rank) of each equation in the model file needs to correspond to the response category that is represented at that position/rank in the data
. The mapping of data to response category is done via position. The ordinal position (rank) of each equation in the model file needs to correspond to the response category that is represented at that position/rank in the data  or to the column with that number if the data object is a
or to the column with that number if the data object is a  or
or  . If a
. If a  or
or  contains more than one row, each row is considered as one data set, and the MPT model is fitted separately for each data set and the data summed across rows is considered as another data set (called
contains more than one row, each row is considered as one data set, and the MPT model is fitted separately for each data set and the data summed across rows is considered as another data set (called  data set), which is also fitted. The data can be entered directly into R or loaded using one of the data import functions (e.g.,
data set), which is also fitted. The data can be entered directly into R or loaded using one of the data import functions (e.g.,  ; see also R Development Core Team, 2010a). The
; see also R Development Core Team, 2010a). The  data of the data set described below could be entered as vector
data of the data set described below could be entered as vector  as
as
An example session
Before estimating model parameters, it is important to see whether a model is identifiable. As was previously pointed out, the 2HTM as presented in Fig. 1 has three parameters, while the “Old”/”New” responses for both old and new items provide only two independent categories (i.e., independent data points to be fitted) as given in the output of  . This means that the 2HTM with three parameters is not identifiable in the current form. There are two ways of achieving identifiability for this model: (1) by imposing the restriction D
n
= D
o
(Snodgrass & Corwin, 1988) and/or (2) by including additional sets of observed categorical responses and subsequently extending the model in order to account for them.
. This means that the 2HTM with three parameters is not identifiable in the current form. There are two ways of achieving identifiability for this model: (1) by imposing the restriction D
n
= D
o
(Snodgrass & Corwin, 1988) and/or (2) by including additional sets of observed categorical responses and subsequently extending the model in order to account for them.
The extension proposed by the second option can be implemented by fitting the model to responses obtained across different bias conditions, where individuals assumed distinct tendencies to respond “Old” or “New.” These different response biases or tendencies can be induced by changing the proportion of old items in the test phase (e.g., 10 % vs. 90 %), for example. According to the theoretical principles underlying the 2HTM, the guessing parameter g would be selectively affected by a response bias manipulation, with D
o
and D
n
remaining unchanged. For example, Bröder and Schütz (2009) used the second solution sketched above by implementing five separate test phases, each with different proportions of old items (10 %, 25 %, 50 %, 75 %, and 90 %). Consider the resulting model-file  (only the first four trees are depicted):
(only the first four trees are depicted):
and the corresponding output from  showing that there are more degrees of freedom than free parameters:
showing that there are more degrees of freedom than free parameters:
Now consider a 40 × 20 matrix named  containing the individual data of the 40 participants from Bröder and Schütz’s (2009) Experiment 3.Footnote 5 Each participant was tested across five different base-rate conditions (10 %, 25 %, 50 %, 75 %, and 90 % old items). In this data matrix, each row corresponds to one participant, and the columns correspond to the different response categories in the same order as in the model file.
containing the individual data of the 40 participants from Bröder and Schütz’s (2009) Experiment 3.Footnote 5 Each participant was tested across five different base-rate conditions (10 %, 25 %, 50 %, 75 %, and 90 % old items). In this data matrix, each row corresponds to one participant, and the columns correspond to the different response categories in the same order as in the model file.
MPTinR provides two main functions for model fitting and selection,  and
and  ;
;  is the major function for fitting MPT models to data, returning results such as the obtained log-likelihood and G
2 value, the information criteria AIC, BIC, and FIA (if requested), parameter estimates and respective confidence intervals, and predicted response frequencies. Optionally, one can specify model restrictions or request the estimation of the FIA. It has the format
is the major function for fitting MPT models to data, returning results such as the obtained log-likelihood and G
2 value, the information criteria AIC, BIC, and FIA (if requested), parameter estimates and respective confidence intervals, and predicted response frequencies. Optionally, one can specify model restrictions or request the estimation of the FIA. It has the format  Two arguments in the
Two arguments in the  function are of note. First,
function are of note. First,  by default returns the best of five fitting runs for each data set, a number that can be changed with the
by default returns the best of five fitting runs for each data set, a number that can be changed with the  argument. Second, FIA is calculated using Monte Carlo methods (see Wu et al., 2010a, 2010b), with the number of samples to be used being specified by the
argument. Second, FIA is calculated using Monte Carlo methods (see Wu et al., 2010a, 2010b), with the number of samples to be used being specified by the  argument. Following the recommendations of Wu et al., the number of samples should not be below 200,000 for real applications.
argument. Following the recommendations of Wu et al., the number of samples should not be below 200,000 for real applications.
A function that should aid in model selection (e.g., Zucchini, 2000) is  , which takes multiple results from
, which takes multiple results from  as the argument and produces a table comparing the models on the basis of the information criteria AIC, BIC, and FIA. It has the format
as the argument and produces a table comparing the models on the basis of the information criteria AIC, BIC, and FIA. It has the format 
 , where
, where  is a
is a  of results returned by
of results returned by  .
.
In order to exemplify the use of the  and
and  functions, two MPT models are fitted to the data from Bröder and Schütz’s (2009) Experiment 3, the 2HTM model described above, and a restricted version of the 2HTM in which the
functions, two MPT models are fitted to the data from Bröder and Schütz’s (2009) Experiment 3, the 2HTM model described above, and a restricted version of the 2HTM in which the  constraint was imposed (saved in file
constraint was imposed (saved in file  )Footnote 6:
)Footnote 6:
The  function returns a
function returns a  with the
with the 
 (for a detailed description, see
(for a detailed description, see  ). Let us first look at the 2HTM results for aggregated data (which replicate the results in Bröder & Schütz, 2009, Table 4):
). Let us first look at the 2HTM results for aggregated data (which replicate the results in Bröder & Schütz, 2009, Table 4):
Next, we may want to compare the parameter estimates for the aggregated data between the original and inequality restricted models:
As these results show, the order restriction on the guessing parameters held for the aggregated data sets (since the parameter values are identical between the two models), and the parameters values are within reasonable ranges. Note that the order of the parameters is alphabetical (i.e., D n , D o , g 1, g 2, g 3, g 4, g 5). Before comparing the models to decide which to select on the basis of the performance on this data set, we might want to check whether all models provided a reasonable account of the data by inspecting the goodness-of-fit statistics. To this end, we inspect not only the aggregated data, but also the summed individual fits:
The results show that the 2HTM is not grossly misfitting the data, since none of the likelihood ratio tests is rejected (i.e., \( p{\mathrm{s}} > .05 \)). Furthermore, as is implied from the previous results, there are no differences for the aggregated data between the 2HTM with or without the order restriction applied to the guessing parameters. This, however, is not the case for the summed individual data. The log-likelihood and G 2 values for the 2HTM with the order restriction is slightly worse than these values for the original 2HTM, indicating that, at least for some data sets, the order restriction does not hold.
From these findings, the question arises of whether or not the restrictions on the guessing parameters are justified when both model fit and model flexibility are taken into account. To this end, we call  to compare the two models using information criteria (note that we call
to compare the two models using information criteria (note that we call  with
with  to obtain the model selection table for both individual and aggregated data; the default
to obtain the model selection table for both individual and aggregated data; the default  only returns a table comparing the individual results):
only returns a table comparing the individual results):
The returned table compares one model per row (here, split across multiple rows) using the information criteria FIA, AIC, and BIC. For each criterion, delta values (i.e., in reference to the smallest value) and absolute values are presented. The columns labeled  indicate how often each model provided the best account when the individual data sets were compared. As can be seen, for FIA, the model with the order restriction always provided the best account for the individual data sets (40 out of 40 individuals). In contrast, for AIC and BIC, the unrestricted 2HTM provided the best account only for 26 individuals (i.e., 40–14). For 14 individuals, AIC and BIC were identical for both models. Since the number of parameters is identical for both models and the penalty factor of AIC and BIC only includes the number of parameters as a proxy of model complexity, the difference in AIC and BIC between those two models merely reflects their differences in model fit. Furthermore, the table presents AIC and BIC weights (
indicate how often each model provided the best account when the individual data sets were compared. As can be seen, for FIA, the model with the order restriction always provided the best account for the individual data sets (40 out of 40 individuals). In contrast, for AIC and BIC, the unrestricted 2HTM provided the best account only for 26 individuals (i.e., 40–14). For 14 individuals, AIC and BIC were identical for both models. Since the number of parameters is identical for both models and the penalty factor of AIC and BIC only includes the number of parameters as a proxy of model complexity, the difference in AIC and BIC between those two models merely reflects their differences in model fit. Furthermore, the table presents AIC and BIC weights ( and
and  ; Wagenmakers & Farrell, 2004).
; Wagenmakers & Farrell, 2004).
Overall, the results indicate the utility of FIA as a measure for model selection. As was expected, when the order restriction holds (as is the case for the aggregated data), FIA prefers the less complex model (i.e., the one in which the possible parameter space is reduced due to inequality restrictions). This preference for the less complex models is even evident for the cases where the order restriction might not completely hold, since FIA prefers the order-restricted model for all individuals even though the order-restricted model provides a worse fit for 26 individuals. For the data sets obtained by Bröder and Schütz (2009) the more complex (i.e., unrestricted) 2HTM model, albeit providing the better fit, seems unjustifiably flexible when FIA is used as the model selection criterion.
Note that the calculation of FIA is computationally demanding, especially when inequality restrictions are applied (see the Appendix on how the model is reparametrized for inequality restrictions). Obtaining the FIA for the unrestricted model took around 80 s on a 3.4-GHz PC with 8 CPU cores running 32-bit Windows 7™ (all timing results reported in this article were done using this computer). In contrast, obtaining the FIA for the order-restricted model took 7 min 40 s. Note that these values include the fitting time, which is negligible, as compared with the time for computing the FIA. Fitting all 40 individuals to the unrestricted 2HTM model takes 3 s, and to the order-restricted 2HTM model 12 s.
Bootstrapping
Besides model fitting and model selection, the next major functionality of MPTinR concerns bootstrap simulation (Efron & Tibshirani, 1994). In the previous example using the individual data sets obtained by Bröder and Schütz (2009), the response frequencies were low, due to the small number of trials. In such cases, asymptotic statistics such as the sampling distribution of the G 2 statistic or the asymptotic confidence intervals for the parameter estimates can be severely compromised (e.g., Davis-Stober, 2009). Another situation that compromises the assumptions underlying those asymptotic statistics is when parameter estimates are close to the boundaries of the parameter space (i.e., near to 0 or 1; Silvapulle & Sen, 2005). In such cases, the use of bootstrap simulations may overcome these problems.
According to the bootstrap principle (Efron & Tibshirani, 1994), if one assumes that an observed data sample \( \widehat{F} \), randomly drawn from a probability distribution F, provides a good characterization of the latter, then one can evaluate F by generating many random samples (with replacement) from \( \widehat{F} \) and treating them as “replications” of \( \widehat{F} \). These bootstrap samples can then be used to draw inferences regarding the model used to fit the data, such as obtaining standard errors for the model’s parameter estimates (\( \widehat{\varTheta } \)). When the data samples are generated on the basis of the observed data and no assumption is made regarding the adequacy of the model to be fitted, the bootstrap is referred to as nonparametric. Alternatively, bootstrap samples can be based on the model’s parameter estimates that were obtained with the original data. In this case, the model is assumed to correspond to the true data-generating process, and the bootstrap is designated as parametric. The parametric bootstraps can be used to evaluate the sampling distribution of several statistics such as the G 2 and the p-values under distinct hypotheses or models (Efron & Tibshirani, 1994; see also van de Schoot, Hoijtink, & Dekovic, 2010). The use of the parametric and nonparametric bootstraps provides a way not only to overcome the limitations of asymptotic statistics, but also to evaluate parameter estimates and statistics under distinct assumptions.
MPTinR contains two higher level functions,  and
and  , that can be used for bootstrap simulations. The function
, that can be used for bootstrap simulations. The function  produces bootstrap samples based on a given model and a set of parameter values. The function
produces bootstrap samples based on a given model and a set of parameter values. The function  produces bootstrap samples based on a given data set. These functions can be used separately or jointly in order to obtain parametric and nonparametric bootstrap samples. These are general purpose functions that can be used for a wide variety of goals, such as (1) obtaining confidence intervals for the estimated parameters, (2) sampling distributions of the G
2 statistic and p-values under several types of null-hypotheses (van de Schoot et al., 2010), and (3) model-mimicry analysis (Wagenmakers, Ratcliff, Gomez, & Iverson, 2004). Also, bootstrap simulations assuming individual differences, as implemented by Hu and Phillips (1999) and Moshagen (2010), can be obtained using these functions. Both functions are calling R’s
produces bootstrap samples based on a given data set. These functions can be used separately or jointly in order to obtain parametric and nonparametric bootstrap samples. These are general purpose functions that can be used for a wide variety of goals, such as (1) obtaining confidence intervals for the estimated parameters, (2) sampling distributions of the G
2 statistic and p-values under several types of null-hypotheses (van de Schoot et al., 2010), and (3) model-mimicry analysis (Wagenmakers, Ratcliff, Gomez, & Iverson, 2004). Also, bootstrap simulations assuming individual differences, as implemented by Hu and Phillips (1999) and Moshagen (2010), can be obtained using these functions. Both functions are calling R’s  function to obtain multinomially distributed random data.
function to obtain multinomially distributed random data.
Given the variety of bootstrap methods and their goals (Efron & Tibshirani, 1994), we provide only a simple example in which 10,000 parametric bootstrap samples are used to estimate the 95 % confidence intervals for the parameter estimates obtained with the aggregated data from Bröder and Schütz (2009):
In this example, we first fit the original data to the (unrestricted) 2HTM to obtain parameter estimates. These estimates are displayed (along with the asymptotic confidence intervals based on the Hessian matrix) and then used as an argument to the  function, requesting 10,000 bootstrap samples. In the next step, the bootstrap samples are fitted using
function, requesting 10,000 bootstrap samples. In the next step, the bootstrap samples are fitted using  , setting the
, setting the  argument to
argument to  to prevent MPTinR from trying to fit the (meaningless) aggregated data set. Finally, the 95 % confidence intervals are calculated by obtaining the 2.5 % and 97.5 % quantile from the resulting distribution of estimates for each parameter (conveniently done using R’s
to prevent MPTinR from trying to fit the (meaningless) aggregated data set. Finally, the 95 % confidence intervals are calculated by obtaining the 2.5 % and 97.5 % quantile from the resulting distribution of estimates for each parameter (conveniently done using R’s  function). As can be seen, the Hessian-based confidence intervals and bootstrapped confidence intervals strongly agree, indicating that the variance–covariance matrix obtained via the Hessian matrix is a good approximation of the true variance–covariance matrix (see Hu & Phillips, 1999).
function). As can be seen, the Hessian-based confidence intervals and bootstrapped confidence intervals strongly agree, indicating that the variance–covariance matrix obtained via the Hessian matrix is a good approximation of the true variance–covariance matrix (see Hu & Phillips, 1999).
Fitting the 10,000 samples took 9 min. Using the multicore functionality of MPTinR (which is more thoroughly described below and in the documentation of  ) and all available eight CPUs, the fitting time was reduced to below 2 min. Note that all the other commands in this example were executed almost instantaneously. For obtaining nonparametric confidence intervals, the call to
) and all available eight CPUs, the fitting time was reduced to below 2 min. Note that all the other commands in this example were executed almost instantaneously. For obtaining nonparametric confidence intervals, the call to  should be replaced with a call to
should be replaced with a call to  —for example,
—for example, 
 (see also the supplemental material).
(see also the supplemental material).
Additional functionality
This section gives an overview of the additional functions in MPTinR, besides the main functions described above (see also Table 1). As was already sketched above, MPTinR can fit many types of cognitive models. The  function is a copy of
function is a copy of  (i.e., a model needs to be defined in a model file), with the additional possibility of specifying upper and lower bounds for the parameters (as, for example, is needed to fit SDT models). Its documentation contains an example of fitting an SDT model to the data of Bröder and Schütz (2009). The
(i.e., a model needs to be defined in a model file), with the additional possibility of specifying upper and lower bounds for the parameters (as, for example, is needed to fit SDT models). Its documentation contains an example of fitting an SDT model to the data of Bröder and Schütz (2009). The  function allows for even more flexibility in representing a model. Instead of a model file, a model needs to be specified as an R function returning the log-likelihood of the model (known as an objective function), which will be minimized. This allows one to fit models to categorical data that cannot be specified in model files—for example, models containing integrals. The documentation of
function allows for even more flexibility in representing a model. Instead of a model file, a model needs to be specified as an R function returning the log-likelihood of the model (known as an objective function), which will be minimized. This allows one to fit models to categorical data that cannot be specified in model files—for example, models containing integrals. The documentation of  contains an example of how to fit an SDT model to a recognition memory experiment in which memory performance is measured via a ranking task (Kellen, Klauer, & Singmann, 2012). Actually,
contains an example of how to fit an SDT model to a recognition memory experiment in which memory performance is measured via a ranking task (Kellen, Klauer, & Singmann, 2012). Actually,  is called by
is called by  and
and  with objective functions created for the models in the model file. The
with objective functions created for the models in the model file. The  function is the old version of MPTinR’s main function containing a different fitting algorithm (see its documentation for more information). Note that
function is the old version of MPTinR’s main function containing a different fitting algorithm (see its documentation for more information). Note that  accepts results from any of the fitting functions in MPTinR (since all output is produced by
accepts results from any of the fitting functions in MPTinR (since all output is produced by  ). To reduce computational time for large data sets or models, MPTinR contains the possibility of using multiple processors or a computer cluster by parallelizing the fitting algorithm, using the snowfall package (Knaus, Porzelius, Binder, & Schwarzer, 2009). Furthermore, fitting of the aggregated data set can be disabled by setting
). To reduce computational time for large data sets or models, MPTinR contains the possibility of using multiple processors or a computer cluster by parallelizing the fitting algorithm, using the snowfall package (Knaus, Porzelius, Binder, & Schwarzer, 2009). Furthermore, fitting of the aggregated data set can be disabled by setting  .
.
In addition to the data-generating functions  and
and  described in the previous section, the function
described in the previous section, the function  returns predicted response proportions or predicted data from a vector of parameter values for a given model. This function can be used to check whether a model recovers certain parameter values (i.e., by fitting the predicted responses) and simulated identifiability (i.e., repeating this step multiple times with random parameter values; Rouder & Batchelder, 1998). The function
returns predicted response proportions or predicted data from a vector of parameter values for a given model. This function can be used to check whether a model recovers certain parameter values (i.e., by fitting the predicted responses) and simulated identifiability (i.e., repeating this step multiple times with random parameter values; Rouder & Batchelder, 1998). The function  internally calls
internally calls  . Note that the data-generating functions that take a model as an argument also work with any model that can be specified in a model file, such as signal detection models.
. Note that the data-generating functions that take a model as an argument also work with any model that can be specified in a model file, such as signal detection models.
The  function is our R port of the original
function is our R port of the original  function from Wu and colleagues (2010a). Since
function from Wu and colleagues (2010a). Since  requires a model to be entered as a word in \( {{\mathrm{L}}_{\mathrm{BMPT}}} \), we provide the convenience function
requires a model to be entered as a word in \( {{\mathrm{L}}_{\mathrm{BMPT}}} \), we provide the convenience function  , which takes similar arguments as
, which takes similar arguments as  and will call
and will call  with the correct arguments. Since the original
with the correct arguments. Since the original  in MATLAB is faster than its R port, in some cases, researchers might prefer to obtain the FIA from MATLAB. To this end, MPTinR contains the convenience function
in MATLAB is faster than its R port, in some cases, researchers might prefer to obtain the FIA from MATLAB. To this end, MPTinR contains the convenience function  . It takes the same arguments as
. It takes the same arguments as  but will return a string that is the call to the original
but will return a string that is the call to the original  function in MATLAB (i.e., the string just needs to be copied and pasted into MATLAB). As was noted above, the FIA can be directly computed in a call to
function in MATLAB (i.e., the string just needs to be copied and pasted into MATLAB). As was noted above, the FIA can be directly computed in a call to  (if one wants to use
(if one wants to use  , it is necessary to use
, it is necessary to use  and not the other just described functions).
and not the other just described functions).
Finally, MPTinR contains three helper functions. The  function will take a model file as an argument and will produce a word in \( {{\mathrm{L}}_{\mathrm{BMPT}}} \), using the algorithm described above. The
function will take a model file as an argument and will produce a word in \( {{\mathrm{L}}_{\mathrm{BMPT}}} \), using the algorithm described above. The  function will take a model file in
function will take a model file in  format and will produce a file in the EQN format. Similarly,
format and will produce a file in the EQN format. Similarly,  will take data (either a single
will take data (either a single  or a
or a  ) and will produce a single file in the MDT format containing all the data sets. EQN and MDT files are used by other programs for fitting MPT models such as MultiTree (Moshagen, 2010) or HMMTree (Stahl & Klauer, 2007).
) and will produce a single file in the MDT format containing all the data sets. EQN and MDT files are used by other programs for fitting MPT models such as MultiTree (Moshagen, 2010) or HMMTree (Stahl & Klauer, 2007).
Comparison of MPTinR and related software
In the last section of this article, we wish to compare MPTinR with the other contemporary software packages for fitting MPT models—namely, multiTree (Moshagen, 2010) and HMMTree (Stahl & Klauer, 2007)—highlight which software might be used for which use case, and provide an outlook of the future of MPTinR. The major difference between MPTinR and the software packages referred to above is that MPTinR is couched within the R programming language, whereas the others are standalone software. As such, MPTinR is a highly flexible software package, given that it allows (and encourages) the implementation of new features by any user. Since the source code of the other two softwares is not directly available, it is difficult to foresee how easily additional features can be added by users other than the original authors. Additionally, MPTinR is the only software that provides a full analysis of multiple data sets including summed individual results and analysis of the aggregated data. HMMtree analyzes only the aggregated data, and multiTree analyzes only the individual data (without providing summed fitting indices). However, MPTinR has several shortcomings in terms of performance and implemented features.
HMMTree is the only software that allows for latent class MPT models (Klauer, 2006). Furthermore, its optimization routine is based on an optimized EM-algorithm implemented in Fortran (K. C. Klauer, personal communication, July 2, 2011), and hence, it is potentially faster than other algorithms based on virtual machines (i.e., multiTree) or interpreted languages (i.e., MPTinR). In fact, a comparison of all three software packages, using a rather complex MPT model consisting of 1 tree with 16 response categories (the dual-process model of conditional reasoning [Oberauer, 2006] using data set DF, Table 4, n = 557), reveals that HMMTree is the fastest. Whereas MPTinR and multiTree are comparable (both finish in under a second), the results of HMMTree appear instantaneous. Note that the timing of HMMTree and multiTree is slightly difficult, since they provide no timing of the fitting process and, hence, it has to be done by hand. However, HMMTree only allows for the fitting of models that are members of \( {{\mathrm{L}}_{\mathrm{BMPT}}} \) (Purdy & Batchelder, 2009). Furthermore, the software does not provide the wealth of surrounding functionalities, such as convenient model specification, parameter restrictions, model selection, and data generation. In addition, HMMTree can be used only on MS Windows™.
The multiTree software comes with a wide set of features that are comparable or even extend the possibilities of MPTinR. Especially, multiTree is the only software that provides a visual model builder, which can be especially useful for occasional users of MPT models. Similarly, all functionalities are available via a graphical user interface that makes it appealing to nonprogrammers. Furthermore, multiTree now also allows for the computation of FIA (to set the number of Monte Carlo samples for the computation of FIA, the default is 100,000; one needs to modify the multiTree  file located in the user home directory; M. Moshagen, personal communication, July 20, 2012). Finally, there are two unique features of multiTree that MPTinR currently lacks—namely, the ability to use other divergence statistics (see Footnote 1) and to perform power analyses. On the other hand, multiTree contains no model selection functionality other than comparing two nested models and can deal only with models that are members of \( {{\mathrm{L}}_{\mathrm{BMPT}}} \), which limits its use when more complex MPT and signal-detection models are compared (e.g., Klauer & Kellen, 2010). Furthermore, although multiTree comes with a wealth of bootstrap functions, it misses the flexibility of MPTinR. For example, it seems difficult to implement model mimicry analysis (Wagenmakers et al., 2004) or double-bootstrap procedures to assess p-values in inequality-restricted inference tests (van de Schoot et al., 2010), while such procedures can be implemented in MPTinR in a relatively straightforward manner through the use of the
file located in the user home directory; M. Moshagen, personal communication, July 20, 2012). Finally, there are two unique features of multiTree that MPTinR currently lacks—namely, the ability to use other divergence statistics (see Footnote 1) and to perform power analyses. On the other hand, multiTree contains no model selection functionality other than comparing two nested models and can deal only with models that are members of \( {{\mathrm{L}}_{\mathrm{BMPT}}} \), which limits its use when more complex MPT and signal-detection models are compared (e.g., Klauer & Kellen, 2010). Furthermore, although multiTree comes with a wealth of bootstrap functions, it misses the flexibility of MPTinR. For example, it seems difficult to implement model mimicry analysis (Wagenmakers et al., 2004) or double-bootstrap procedures to assess p-values in inequality-restricted inference tests (van de Schoot et al., 2010), while such procedures can be implemented in MPTinR in a relatively straightforward manner through the use of the  and
and  functions.
functions.
Like most R packages, MPTinR is continuously under development. New functionalities will be added, and previous ones improved. The implementation of hierarchical MPT modeling (Klauer, 2006, 2009; Smith & Batchelder, 2010) is of special importance, since it overcomes well-known limitations associated to fitting individual and aggregated data and is able to account for item effects as well (Baayen, Davidson, & Bates, 2008). We intend to include additional features (as well as improve current ones) in future versions of MPTinR (see https://r-forge.r-project.org/projects/mptinr/ for development versions of MPTinR). Since the source code of MPTinR is already freely available and MPTinR is hosted on R-Forge, a platform for the collaborative development of R software (Theußl & Zeileis, 2009), this further development is not restricted to the present authors. In fact, we would happily welcome interested researchers joining in the development of MPTinR.
Notes
Parameter estimation in MPTinR can be made only by using the maximum-likelihood method (Equation 6), which can be obtained by minimizing the discrepancies between observed and expected response frequencies as measured by the G 2 statistic (Equation 7; Bishop, Fienberg, & Holland, 1975). As pointed out by a reviewer, instead of minimizing the G 2 statistic, other discrepancy statistics can be used—in particular, one of the many possible statistics coming from the power-divergence family (Read & Cressie, 1988), of which the G 2 is a special case. Studies (e.g., García-Pérez, 1994; Riefer & Batchelder, 1991) have shown that some of these statistics can be advantageous when dealing with sparse data and attempting to minimize a model’s sensitivity to outliers. Still, the use of alternatives to the G 2 statistic coming from the power-divergence family has several shortcomings. First, it is not clear which particular statistic would be more advantageous for a specific type of MPT model and data, a situation that would require an extensive evaluation of different alternative statistics. Second, the use of an alternative to the G 2 statistic represents a dismissal of the maximum-likelihood method, which, in turn, compromises the use of popular model selection measures such as the Akaike information criterion, the Bayesian information Criterion, or the Fisher information approximation (which will be discussed in detail later), all of which assume the use of the maximum-likelihood method. Given these disadvantages and the almost ubiquitous use of maximum-likelihood estimation in MPT modeling (for reviews, see Batchelder & Riefer, 1999; Erdfelder et al., 2009), the current version of MPTinR only implements the maximum-likelihood method for parameter estimation and the G 2 statistic for quantification of model misfit.
In the AIC and BIC formulas, the first term corresponds to the model’s goodness of fit, and the second additive term to the model’s penalty factor. As was noted by one of the reviewers, we use the G 2 as the first term, contrary to other implementations that use the models’ log-likelihood (LL M ) instead. G 2 corresponds to \( 2 \times (L{L_S} - L{L_M}) \), with LL S being the log-likelihood of a saturated model that perfectly describes the data. In this sense, the definitions of AIC and BIC given in the main body of the text can be viewed as differences in AIC and BIC between these two models, making the notation \( \Delta {\rm{AIC}} \) and \( \Delta {\rm{BIC}} \) more appropriate. We nevertheless use the notation AIC and BIC, given that we use the notation \( \Delta {\rm{AIC}} \) and \( \Delta {\rm{BIC}} \) when referring to differences between different candidate models other than the saturated model that perfectly describes the data.
Note that the way MPTinR deals with comments has changed. As is common in R (and other programming languages), everything to the right of the comment symbol # is ignored. In previous versions or MPTinR (prior to version 0.9.2), a line containing a # at any position was ignored completely.
R looks for files in the current working directory. To find out what is the current working directory, type
 at the R prompt. You can change the working directory using either the R menu or the
at the R prompt. You can change the working directory using either the R menu or the  function. Additionally, models and restrictions can also be specified within an R script (i.e., not in a file) using a
function. Additionally, models and restrictions can also be specified within an R script (i.e., not in a file) using a  (see the examples in
(see the examples in  and
and  ).
).We thank Arndt Bröder for providing this data set, which also comes with MPTinR. It can be loaded via
 and is then available as
and is then available as  . The other files necessary to fit these data (i.e., the model and restriction files) also come with MPTinR (see
. The other files necessary to fit these data (i.e., the model and restriction files) also come with MPTinR (see  ).
).To fit only the
 data entered before as
data entered before as  , simply replace
, simply replace  with
with  as in
as in 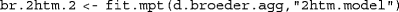 . Additionally, the supplemental material contains extensions of this and the other examples given in the text.
. Additionally, the supplemental material contains extensions of this and the other examples given in the text.
References
Akaike, H. (1974). A new look at the statistical model identification. IEEE Transactions on Automatic Control, 19, 716–723.
Baayen, R., Davidson, D., & Bates, D. (2008). Mixed-effects modeling with crossed random effects for subjects and items. Journal of Memory and Language, 59, 390–412.
Baldi, P., & Batchelder, W. H. (2003). Bounds on variances of estimators for multinomial processing tree models. Journal of Mathematical Psychology, 47, 467–470.
Bamber, D., & van Santen, J. (1985). How many parameters can a model have and still be testable? Journal of Mathematical Psychology, 29, 443–473.
Batchelder, W. H., & Riefer, D. M. (1999). Theoretical and empirical review of multinomial process tree modeling. Psychonomic Bulletin & Review, 6, 57–86.
Becker, R. A., Chambers, J. M., & Wilks, A. R. (1988). The new S language: A programming environment for data analysis and graphics. Pacific Grove, Calif: Wadsworth & Brooks/Cole Advanced Books & Software.
Bishop, Y. M. M., Fienberg, S. E., & Holland, P. W. (1975). Discrete multivariate analysis: Theory and practice. Cambridge, Mass: MIT Press.
Bröder, A., & Schütz, J. (2009). Recognition ROCs are curvilinear-or are they? On premature arguments against the two-high-threshold model of recognition. Journal of Experimental Psychology: Learning, Memory, and Cognition, 35, 587.
Byrd, R. H., Lu, P., Nocedal, J., & Zhu, C. (1995). A limited memory algorithm for bound constrained optimization. SIAM J. Sci. Comput., 16(5), 1190–1208.
Davis-Stober, C. P. (2009). Analysis of multinomial models under inequality constraints: Applications to measurement theory. Journal of Mathematical Psychology, 53, 1–13.
Efron, B., & Tibshirani, R. (1994). An introduction to the bootstrap. New York: Chapman & Hall.
Erdfelder, E., Auer, T., Hilbig, B. E., Aßfalg, A., Moshagen, M., & Nadarevic, L. (2009). Multinomial processing tree models. Zeitschrift fur Psychologie / Journal of Psychology, 217, 108–124.
García-Pérez, M. A. (1994). Parameter estimation and goodness-of-fit testing in multinomial models. British Journal of Mathematical and Statistical Psychology, 47, 247–282.
Green, D. M., & Swets, J. A. (1966). Signal detection theory and psychophysics. New York: Wiley.
Grünwald, P. D. (2007). The minimum description length principle. Cambridge, Mass: MIT Press.
Hu, X., & Batchelder, W. H. (1994). The statistical analysis of general processing tree models with the EM algorithm. Psychometrika, 59, 21–47.
Hu, X., & Phillips, G. A. (1999). GPT.EXE: A powerful tool for the visualization and analysis of general processing tree models. Behavior Research Methods, Instruments, & Computers, 31, 220–234.
Kaufman, L., & Gay, D. (2003). The PORT Library - Optimization. Murray Hill, NJ: AT&T Bell Laboratories.
Kellen, D., & Klauer, K. C. (2011). Evaluating models of recognition memory using first- and second-choice responses. Journal of Mathematical Psychology, 55, 251–266.
Kellen, D., Klauer, K. C., & Singmann, H. (2012). On the measurement of criterion noise in signal detection theory: The case of recognition memory. Psychological Review, 119, 457–479.
Klauer, K. C. (2006). Hierarchical multinomial processing tree models: A Latent-Class approach. Psychometrika, 71(1), 7–31.
Klauer, K. C. (2009). Hierarchical multinomial processing tree models: A Latent-Trait approach. Psychometrika, 75, 70–98.
Klauer, K. C., & Kellen, D. (2010). Toward a complete decision model of item and source recognition: A discrete-state approach. Psychonomic Bulletin & Review, 17, 465–478.
Klauer, K. C., & Kellen, D. (2011). The flexibility of models of recognition memory: An analysis by the minimum-description length principle. Journal of Mathematical Psychology, 55, 430–450.
Knapp, B. R., & Batchelder, W. H. (2004). Representing parametric order constraints in multi-trial applications of multinomial processing tree models. Journal of Mathematical Psychology, 48, 215–229.
Knaus, J., Porzelius, C., Binder, H., & Schwarzer, G. (2009). Easier parallel computing in R with snowfall and sfCluster. The R Journal, 1, 54–59.
Macmillan, N. A., & Creelman, C. D. (2005). Detection theory: A user’s guide. New York: Lawrence Erlbaum associates.
Moshagen, M. (2010). multiTree: A computer program for the analysis of multinomial processing tree models. Behavior Research Methods, 42, 42–54.
Muenchen, R. A. (2012, January 4). The popularity of data analysis software [Web log message]. Retrieved from http://r4stats.com/popularity
Myung, I. J., Forster, M. R., & Browne, M. W. (2000). Guest Editors’ Introduction: Special issue on model selection. Journal of Mathematical Psychology, 44, 1–2.
Oberauer, K. (2006). Reasoning with conditionals: A test of formal models of four theories. Cognitive Psychology, 53, 238–283.
Purdy, B. P. (2011). Coding graphical models: Probabilistic context free languages & the minimum description length principle.
Purdy, B. P., & Batchelder, W. H. (2009). A context-free language for binary multinomial processing tree models. Journal of Mathematical Psychology, 53, 547–561.
R Development Core Team (2012a). R Data Import/Export. Number 3-900051-10-0. R Foundation for Statistical Computing, Vienna, Austria. ISBN 3-900051-07-0.
R Development Core Team (2012b). R: A Language and Environment for Statistical Computing. Vienna, Austria. ISBN 3-900051-07-0.
Rödiger, S., Friedrichsmeier, T., Kapat, P., & Michalke, M. (2012). RKWard: A comprehensive graphical user interface and integrated development environment for statistical analysis with r. Journal of Statistical Software, 49(9), 1–34.
Read, T., & Cressie, N. (1988). Goodness-of-fit statistics for discrete multivariate data. New York: Springer.
Riefer, D. M., & Batchelder, W. H. (1988). Multinomial modeling and the measurement of cognitive processes. Psychological Review, 95, 318–339.
Riefer, D. M., & Batchelder, W. H. (1991). Statistical inference for multinomial processing tree models. In J.-P. Doignon & J.-C. Falmagne (Eds.), Mathematical psychology: Current developments, page 313–335. Berlin: Springer.
Roberts, S., & Pashler, H. (2000). How persuasive is a good fit? a comment on theory testing. Psychological Review, 107, 358–367.
Rouder, J. N. and Batchelder, W. H. (1998). Multinomial models for measuring storage and retrieval processes in paired associate learning. pages 195–225. Lawrence Erlbaum Associates Publishers, Mahwah, NJ, US.
Schmittmann, V. D., Dolan, C. V., Raijmakers, M. E. J., & Batchelder, W. H. (2010). Parameter identification in multinomial processing tree models. Behavior Research Methods, 42, 836–846.
Schwarz, G. (1978). Estimating the dimension of a model. The annals of statistics, 6, 461–464.
Silvapulle, M. J., & Sen, P. K. (2005). Constrained statistical inference: Inequality, order, and shape restrictions. Hoboken, N.J.: Wiley-Interscience.
Smith, J. B., & Batchelder, W. H. (2010). Beta-MPT: Multinomial processing tree models for addressing individual differences. Journal of Mathematical Psychology, 54, 167–183.
Snodgrass, J. G., & Corwin, J. (1988). Pragmatics of measuring recognition memory: Applications to dementia and amnesia. Journal of Experimental Psychology: General, 117(1), 34–50.
Stahl, C., & Klauer, K. C. (2007). HMMTree: A computer program for latent-class hierarchical multinomial processing tree models. Behavior Research Methods, 39, 267–73.
Stahl, C., & Klauer, K. C. (2008). A simplified conjoint recognition paradigm for the measurement of gist and verbatim memory. Journal of Experimental Psychology: Learning, Memory, and Cognition, 34, 570–586.
Su, Y., Myung, I. J., & Pitt, M. A. (2005). Minimum description length and cognitive modeling. In P. D. Grünwald, I. J. Myung, & M. A. Pitt (Eds.), Advances in minimum description length: Theory and applications, pages 411–433. Cambridge, Mass: MIT Press.
Theußl, S., & Zeileis, A. (2009). Collaborative software development using R-Forge. The R Journal, 1, 9–14.
Valero-Mora, P. M., & Ledesma, R. (2012). Graphical user interfaces for R. Journal of Statistical Software, 49, 1–8.
van de Schoot, R., Hoijtink, H., & Dekovic, M. (2010). Testing inequality constrained hypotheses in SEM models. Structural Equation Modeling, 17, 443–463.
Vance, A. (2009, January 7). Data analysts captivated by R's power. The New York Times. Retrieved from http://www.nytimes.com/2009/01/07/technology/business-computing/07program.html
Wagenmakers, E., & Farrell, S. (2004). AIC model selection using akaike weights. Psychonomic Bulletin & Review, 11(1), 192–196.
Wagenmakers, E., Ratcliff, R., Gomez, P., & Iverson, G. J. (2004). Assessing model mimicry using the parametric bootstrap. Journal of Mathematical Psychology, 48(1), 28–50.
Wagenmakers, E., & Waldorp, L. (2006). Guest Editors’ Introduction: Special issue on model selection. Journal of Mathematical Psychology, 50, 99–100.
Wu, H., Myung, J. I., & Batchelder, W. H. (2010a). Minimum description length model selection of multinomial processing tree models. Psychonomic Bulletin & Review, 17, 275–286.
Wu, H., Myung, J. I., & Batchelder, W. H. (2010b). On the minimum description length complexity of multinomial processing tree models. Journal of Mathematical Psychology, 54, 291–303.
Zucchini, W. (2000). An introduction to model selection. Journal of Mathematical Psychology, 44, 41–61.
Author note
This work was supported by Grant KL 614/33-1 to Karl Christoph Klauer and Sieghard Beller from the Deutsche Forschungsgemeinschaft (DFG) as part of the priority program “New Frameworks of Rationality” (SPP 1516). Furthermore, this work was supported by grant Kl 614/32-1 from the Deutsche Forschungsgemeinschaft to Karl Christoph Klauer. We thank Karl Christoph Klauer and Fabian Hölzenbein for their comments throughout the development of the described software and Kerstin Dittrich, Xiangen Hu, Gregory Francis, Andreas Kappes, Karl Christoph Klauer, Morten Moshagen, and Alexandra Schulz for comments on earlier versions of this manuscript. Furthermore, we thank the R Development Core Team for their continuing and invaluable efforts to provide R.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
ESM 1
(ZIP 3.27 kb)
Appendix
Appendix
MPTinR algorithms
The purpose of this section is to give an overview of the algorithms used by MPTinR, since they diverge from the usual employed fitting algorithm for MPT models (the EM algorithm; Hu & Batchelder, 1994). Readers mainly interested in using MPTinR for fitting MPT models may skip this section. The main task of MPTinR is model fitting—that is, iteratively finding the maximum likelihood parameter estimates \( \widehat{\varTheta } \). Instead of the EM algorithm, MPTinR uses the general purpose optimization algorithm implemented in R’s  function. This algorithm is a variation of Newton’s method that can use the analytical or approximated (i.e., quasi-Newton) gradient or Hessian to obtain the optimal parameters within parameter bounds and is part of the PORT library (Kaufman & Gay 2003). Previous versions of MPTinR used a different optimization algorithm (L-BFGS-B; Byrd, Lu, Nocedal, & Zhu, 1995), which is still available in the function
function. This algorithm is a variation of Newton’s method that can use the analytical or approximated (i.e., quasi-Newton) gradient or Hessian to obtain the optimal parameters within parameter bounds and is part of the PORT library (Kaufman & Gay 2003). Previous versions of MPTinR used a different optimization algorithm (L-BFGS-B; Byrd, Lu, Nocedal, & Zhu, 1995), which is still available in the function  . However, since L-BFGS-B cannot use an analytical gradient, we changed the algorithm to
. However, since L-BFGS-B cannot use an analytical gradient, we changed the algorithm to  .
.
The advantages of using a general purpose optimization routine instead of a specialized one are twofold. First, the PORT routines are implemented reasonably quickly in the FORTRAN programming language (as compared with optimization algorithms implemented in pure R code). Second, MPTinR does not require a model to strictly follow an MPT form as described in Riefer and Batchelder (1988) or Purdy and Batchelder (2009). Instead, MPTinR literally uses the right-hand sides of the model equations (e.g., Equations 1–4) and evaluates them using the current parameter values at each iteration of the optimization process. In other words, the model is not transformed into any matrix notation (see Riefer & Batchelder, 1988). Consequently, MPTinR can fit any model that can be described in a model file using (inbuilt or self-written) R functions.
When calling  or
or  , the following steps are performed for obtaining \( \widehat{\varTheta } \). The equations in the model file are parsed line by line into R
, the following steps are performed for obtaining \( \widehat{\varTheta } \). The equations in the model file are parsed line by line into R  s (i.e., code that can be executed). These
s (i.e., code that can be executed). These  are concatenated to obtain the likelihood function for a given model (Equation 6). To avoid numerical underflows, the negative log of the likelihood function gives the objective function (i.e., the function that will be minimized). From this function, the functions for calculating the gradient and the Hessian matrix of the model are derived using symbolical derivation implemented in the
are concatenated to obtain the likelihood function for a given model (Equation 6). To avoid numerical underflows, the negative log of the likelihood function gives the objective function (i.e., the function that will be minimized). From this function, the functions for calculating the gradient and the Hessian matrix of the model are derived using symbolical derivation implemented in the  function. The objective, gradient, and Hessian functions are then passed as arguments to
function. The objective, gradient, and Hessian functions are then passed as arguments to  , the workhorse of MPTinR. Also,
, the workhorse of MPTinR. Also,  can be called directly with an objective function if it cannot be specified in a model file.
can be called directly with an objective function if it cannot be specified in a model file.
Both the objective and the gradient functions are per default passed to  for obtaining \( \widehat{\varTheta } \). In cases where
for obtaining \( \widehat{\varTheta } \). In cases where  does not converge successfully, fitting is restarted using a numerically approximated gradient (with warning). Furthermore,
does not converge successfully, fitting is restarted using a numerically approximated gradient (with warning). Furthermore,  and
and  allow one to specify whether or not the gradient function or even the Hessian function should be passed to nlminb (using the Hessian function for fitting improved neither the speed nor the quality of the fitting of MPT models and is, therefore, deactivated per default). To allow an assessment of the quality of the fitting algorithm, MPTinR reports the
allow one to specify whether or not the gradient function or even the Hessian function should be passed to nlminb (using the Hessian function for fitting improved neither the speed nor the quality of the fitting of MPT models and is, therefore, deactivated per default). To allow an assessment of the quality of the fitting algorithm, MPTinR reports the  statistic of a vector containing the values of the objective function at the obtained minima for each fitting run (if
statistic of a vector containing the values of the objective function at the obtained minima for each fitting run (if  ) in output element
) in output element  . Our experience is that the dispersion of the minima is usually 0, unless the data contain many zero cells or the model is not identified for that data set.
. Our experience is that the dispersion of the minima is usually 0, unless the data contain many zero cells or the model is not identified for that data set.
When model restrictions are specified, they will be applied before the objective function is created, in that the expressions representing the model will be altered. In case of equality restrictions (i.e., either setting two parameters equal [e.g., x = y] or fixing a parameter to a value [e.g., x = 0]), the model equations are altered so that the to-be-restricted parameter is replaced with the restriction. To apply inequality restrictions, the model is altered using a variant of method A described by Knapp and Batchelder (2004). More specifically, each instance of the to-be-restricted parameter is replaced by the product of a dummy parameter and the restriction (e.g., for the restriction \( x1 < x2 \), each instance of x1 would be replaced with \( x2 * hank.y1 \)). Note that all dummy parameters in MPTinR start with  ., and therefore, using parameter names starting with these characters should be avoided. Whereas this reparametrization is equivalent to method A of Knapp and Batchelder, it does not preserve the \( {{\mathrm{L}}_{\mathrm{BMPT}}} \) structure of the model. In general, it holds that for order restrictions, only the rightmost element remains, and all other parameters will be replaced. Note that confidence intervals around inequality restricted parameters are based on variance bounds of the parameter estimates (i.e., they represent a "worst case scenario"; Baldi & Batchelder, 2003, Equation 19).
., and therefore, using parameter names starting with these characters should be avoided. Whereas this reparametrization is equivalent to method A of Knapp and Batchelder, it does not preserve the \( {{\mathrm{L}}_{\mathrm{BMPT}}} \) structure of the model. In general, it holds that for order restrictions, only the rightmost element remains, and all other parameters will be replaced. Note that confidence intervals around inequality restricted parameters are based on variance bounds of the parameter estimates (i.e., they represent a "worst case scenario"; Baldi & Batchelder, 2003, Equation 19).
For obtaining the FIA, MPTinR first transforms a model into a word in \( {{\mathrm{L}}_{\mathrm{BMPT}}} \) (if a model consists of multiple trees, these are concatenated by joining parameters), which is then passed to our R port of the algorithm by Wu et al. (2010a). If a model is not a member of \( {{\mathrm{L}}_{\mathrm{BMPT}}} \), calculation of the FIA will fail. MPTinR tries to minimize computational time for the FIA by calculating only the penalty factor of the FIA (i.e., the integral in Equation 10) as many times as needed (i.e., as many times as the ratio of the N between tree differs not as many times as N differs).
Since our method of reparameterizing inequality restrictions does not preserve the MPT structure of a given model (i.e., even if it is a member of \( {{\mathrm{L}}_{\mathrm{BMPT}}} \) before the restrictions are applied, it is not thereafter), MPTinR obtains the FIA for inequality restricted models by passing the unrestricted model to the Wu et al. (2010a) algorithm but specifying the restrictions in the corresponding arguments. Whether or not one wants to enforce the restrictions when fitting the model is controlled by the  argument to
argument to  . The default behavior is to enforce the inequality restriction by reparametrizing the model (i.e.,
. The default behavior is to enforce the inequality restriction by reparametrizing the model (i.e.,  is the default). This contrasts with the example given by Wu et al. (2010a), in which “parameter estimates do not violate” (p. 282) the inequality restrictions and, therefore, the inequality restrictions are not enforced when fitting the model but the restrictions are nevertheless passed to
is the default). This contrasts with the example given by Wu et al. (2010a), in which “parameter estimates do not violate” (p. 282) the inequality restrictions and, therefore, the inequality restrictions are not enforced when fitting the model but the restrictions are nevertheless passed to  . This behavior can be emulated by setting
. This behavior can be emulated by setting  , in which case the inequality restrictions are not enforced when fitting the model but will be taken into account when obtaining the FIA.
, in which case the inequality restrictions are not enforced when fitting the model but will be taken into account when obtaining the FIA.
Rights and permissions
About this article
Cite this article
Singmann, H., Kellen, D. MPTinR: Analysis of multinomial processing tree models in R. Behav Res 45, 560–575 (2013). https://doi.org/10.3758/s13428-012-0259-0
Published:
Issue Date:
DOI: https://doi.org/10.3758/s13428-012-0259-0

















 at the R prompt. You can change the working directory using either the R menu or the
at the R prompt. You can change the working directory using either the R menu or the  function. Additionally, models and restrictions can also be specified within an R script (i.e., not in a file) using a
function. Additionally, models and restrictions can also be specified within an R script (i.e., not in a file) using a  (see the examples in
(see the examples in  and
and  ).
). and is then available as
and is then available as  . The other files necessary to fit these data (i.e., the model and restriction files) also come with MPTinR (see
. The other files necessary to fit these data (i.e., the model and restriction files) also come with MPTinR (see 
 data entered before as
data entered before as 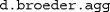 , simply replace
, simply replace  with
with 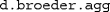 as in
as in 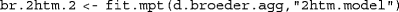 . Additionally, the supplemental material contains extensions of this and the other examples given in the text.
. Additionally, the supplemental material contains extensions of this and the other examples given in the text.