From 6 months of age onward, humans are able to differentiate arrays of dots that differ in numerosity by a ratio of 1:2 (see, e.g., McCrink & Wynn, 2007; Xu & Spelke, 2000; Xu, Spelke, & Goddard, 2005). The acuity with which people can differentiate numerosities increases with age up to a ratio of approximately 7:8 (Halberda & Feigenson, 2008; Piazza et al., 2010; Pica, Lemer, Izard, & Dehaene, 2004; van Oeffelen & Vos, 1982). Electrophysiological studies in monkeys (Nieder, Freedman, & Miller, 2002; Nieder & Miller, 2003) have shown that the presentation of a quantity induces an activation pattern with a Gaussian shape. Thus, a specific numerosity activates a group of cells tuned for this quantity and, to a lesser extent, activates cells encoding for a quantity that is numerically close. Similar results have been shown in human magnetic resonance imaging (MRI) adaptation studies (Piazza, Izard, Pinel, Le Bihan, & Dehaene, 2004; Piazza, Pinel, Le Bihan, & Dehaene, 2007). These studies revealed a decrease in activation with repeated presentation of the same stimulus, followed by an increase when the numerosity changed. Importantly, this increase in activation was dependent on the numerical distance between the repeated and novel numbers. Together, the behavioral studies investigating the acuity of numerosity discrimination and the imaging studies investigating the neural mechanisms underlying numerosity processing have shown a clear relationship between the numerical distance between the numbers presented and behavioral performance and/or neural activity (i.e., the numerical distance effect).

In the field of numerical cognition, the numerical distance effect is the hallmark for number processing: Subjects’ response speed, as well as their accuracy, increases when the distance between two numbers that have to be compared becomes larger (e.g., comparing the numbers 3 and 4 takes more time than comparing 2 and 5; Ansari, Garcia, Lucas, Hamon, & Dhital, 2005; Cohen Kadosh, 2008; Cohen Kadosh, Borodsky, Levin, & Henik, 2008; Moyer & Landauer, 1967; Pinel, Dehaene, Rivière, & LeBihan, 2001; Reynvoet, De Smedt, & Van den Bussche, 2009; Van Opstal, Gevers, De Moor, & Verguts, 2008). It is therefore of fundamental importance that numerical distance and the difference in visual properties of the two nonsymbolic number stimuli that have to be compared not be confounded. To overcome this problem, most previous studies equated the extrinsic variables (e.g., the total area extended by the dots and their total surface)Footnote 1 but randomly varied the intrinsic variables (e.g., the diameter of each dot and the density or interitem spacing) on half of the trials, and did the reverse on the other half of the trials (e.g., Ansari & Dhital, 2006; Izard, Sann, Spelke, & Streri, 2009; Libertus, Woldorff, & Brannon, 2007; Piazza et al., 2007; Santens, Roggeman, Fias, & Verguts, 2010). Although a single visual property, with this approach, becomes less informative about numerosity, it can still significantly co-vary with numerical distance. Furthermore, this design relies on the assumption that when a subject uses visual cues, the subject will only rely on a single visual property throughout the whole of the experiment. However, it is equally likely that a subject would switch between different visual properties, depending on the stimulus at hand. For instance, in trials on which the intrinsic variables of two stimuli are equated (e.g., item size), subjects could respond to differences in extrinsic variables (e.g., total surface), and vice versa. Thus, when one cue is uninformative, another might be used. Since little knowledge exists about how a visual display is transformed into a numerosity code, relations between numerical distance and the differences in visual properties of the two nonsymbolic stimuli to be compared would better be avoided in the first place. As will be shown below, this is not possible for all task designs. Therefore, it would be preferable if information about the different visual cues was registered, to conduct post hoc analyses and show that, indeed, number and not visual cues explain the results.

In numerical cognition, there is general agreement that the results obtained to date do measure the ability to discriminate numerosity, rather than visual cues. Nevertheless, occasional reports have suggested otherwise (Feigenson, Carey, & Spelke, 2002; Gebuis & Gevers, in press; Mix, Huttenlocher, & Levine, 2002; Sophian & Chu, 2008). Here, we do not intend to debate whether the nonsymbolic number studies conducted to date could be explained in terms of the visual properties of the stimuli, but instead want to present a program (designed to work with the Psychophysics Toolbox in MATLAB) suitable for generating the stimuli for various nonsymbolic number studies. We hope that this program will then serve as a tool to further investigate nonsymbolic number processes.

Method

To test the program, we created stimuli for the three main paradigms used in numerical cognition: number comparison, priming, and habituation. In the number comparison paradigm, two numbers or two arrays of, for instance, dots are presented either consecutively or simultaneously, and subjects have to judge which of the two stimuli is numerically larger (e.g., Halberda & Feigenson, 2008). In the priming paradigm, two numbers or two arrays of, for instance, dots are presented consecutively. The first of the stimuli is irrelevant for the task at hand; the subjects only have to name the second number or decide whether it is smaller or larger than a reference number (e.g., Reynvoet et al., 2009; Roggeman, Verguts, & Fias, 2007). The habituation paradigm is used to test infants’ numerical abilities by using looking time (e.g., Libertus et al., 2007; Lipton & Spelke, 2003; Xu & Spelke, 2000) or neuroimaging (e.g., Libertus, Pruitt, Woldorff, & Brannon, 2009; Piazza et al., 2004) as a measure. Here, an array of dots is presented several times (hereafter referred to as the standard trials) and occasionally is replaced with an array of dots representing a different numerosity (hereafter referred to as the deviant-number trials).

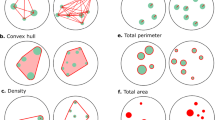
For the comparison and priming paradigms, each stimulus may consist of two dot arrays representing different numbers of dots (hereafter referred to as a number pair; see Fig. 1). We investigated the relation between the numerical distance and the differences in several visual properties of these two dots arrays. In the case of the habituation paradigm, the average of the standard trials was compared with the deviant-number trial following the standards. The following visual properties were taken into account: area extended by a stimulus (or convex hull), total surface (the aggregate value of the different dot surfaces within one display), item size (the average diameter of the different dots within one display), and density (area extended divided by total surface).

Fig. 1
figure 1

Examples of stimulus pairs generated by the program; two stimulus pairs for small and large numerosities are presented. It should be noted that, for visualization purposes only, we equalized the sizes of the images for the small and large numerosities. The sizes of the images are larger when larger numerosities are included in the set

Full size image

Stimuli

The program manipulates the stimulus area (the area in which the dots can appear) as well as the item size (diameter) of the dots. Both the stimulus area and item size were larger in half of the trials and smaller in the other half of the trials for the more numerous array, as compared to the less numerous array. In the comparison and priming paradigms, the stimulus area varied between 75 and 100 percent of the largest stimulus area used. The largest stimulus area was calculated on the basis of the largest numerosity included in the experiment (thus, the stimulus area became larger when larger numerosities were included). Item size differed for the dots within each dot array. To create an array consisting of dots with different item sizes, an item size ranging between 0.11 and 0.79 degrees of visual angleFootnote 2 was randomly assigned to each dot. Because average item size in half of the trials should be larger for the more numerous array and smaller for the less numerous array, item sizes were drawn from a left- or right-skewed distribution, respectively. Consequently, in half of the trials it was more likely that a dot with a large diameter would be included, whereas the reverse was true for the other half of the trials. Importantly, the difference in the visual cues of the two dot arrays would naturally be much larger for trials on which numerosity positively co-varies with the visual properties of the stimuli (e.g., the stimulus with a larger numerosity also has a larger average item size, larger area, smaller density, and larger total surface). Further enhancement of this congruency, by drawing dots from the skewed distributions above, was not desirable, as it would only increase the strength of the relation between visual cues and numerosity. Therefore, in these congruent trials, a less skewed distribution was used for the dot sizes than in the incongruent trials (numerosity negatively co-varied with the visual properties of the stimuli). In contrast to the priming and comparison tasks, the habituation design did not consist of two stimuli per trial, but of a sequence of standards and a deviant-number trial. The standards were constantly varied in terms of their visual properties, except for the last standard, which preceded the deviant-number trial. The size of the area in which the dots could appear and the individual dots sizes of the last standard in the sequence and of the following deviant-number trial were controlled in a manner similar to the one described above. Randomly changing the properties of the visual cues of the standards would make it impossible for the subject to differentiate between standards and deviants based on visual properties alone.

The program (available at http://titiagebuis.eu/Materials.html) has four design options: (1) create all possible combinations of, for instance, 1–5 dots, which results in 25 combinations; (2) make combinations of two numbers, for which one of the two stimuli is, for instance, 24 dots (e.g., 20 dots–24 dots, 12 dots–24 dots, or 24 dots–32 dots); (3) use only the combinations specified (e.g., use only 3 dots–8 dots, 4 dots–7 dots, or 6 dots–3 dots); and (4) repeatedly present, for instance, 24 dots, but occasionally present a deviant number of dots (e.g., 24, 24, 24, 24, 36, 4, 24, 24, 16, 24 . . . ). In the present study, we will only give examples of Designs 2, 3, and 4. These, in contrast to Design 1, allow controlling for numerical distance, meaning that an equal number of trials can be created for each numerical distance. Designs 2, 3, and 4 correspond to the above-described number comparison, priming, and habituation paradigms, respectively.

In numerical cognition, nonsymbolic priming tasks generally include small numerosities (1–4 or 1–9 dots), whereas nonsymbolic comparison tasks include larger numerosities (at least larger than 8 dots). Studies that include small numerosities typically assess the effects on performance of absolute differences between numerosities, whereas those that include large numerosities generally use relative differences. In the latter case, the difference between numerosities is expressed as a proportion of the larger number. For example, the numbers 1 and 4 have an absolute difference of 3, but a relative difference of .75.

Together, the three paradigms used in our experiment were as follows:

  1. (1)

    The priming paradigm, which was based on Design 3. It included the numerosities 1–4 and the absolute differences 1 (combinations 1–2, 3–4, 2–1, 4–3), 2 (combinations 1–3, 2–4, 3–1, 4–2), and 3 (combinations 1–4, 1–4, 4–1, 4–1).

  2. (2)

    The number comparison paradigm, which was based on Design 2 and included the relatively large numerosities 12, 16, 18, 20, 22, 26, 29, 32, 36, and 48 dots, with 24 dots as the standard. Because all numerosities were compared to 24, the relative differences between the numerosities smaller and larger than 24 were comparable.

  3. (3)

    The habituation paradigm, which was based on Design 4 and included the same stimuli used for the comparison paradigm, but now the standard number, 24, was repeated three to seven times before a deviant-number stimulus was presented.

The numbers of trials for the numerical distance conditions in each paradigm were equalized. This resulted in a total of 96 number pairs (32 number pairs for the three absolute-difference condition) for the priming paradigm, and 160 number pairs (32 number pairs for the five relative-difference conditions; thus, the relative-difference conditions smaller and larger than 24 dots were collapsed) for the number comparison and habituation paradigms. The priming paradigm was also conducted using the numbers 4–7 to investigate the effect of small numerosities, which due to their small number do not allow for any, or for only a little, variation in area extended and contour length. For a more elaborate explanation of this problem, see the last paragraph of the Analyses section.

Program features

As mentioned above, the program can generate stimuli for four different designs. These stimuli can be exported as bitmap images. Furthermore, two text files are created that contain the information on each stimulus, as well as the differences in visual and numerical properties of the two stimuli comprising each stimulus pair. The latter can be used to directly investigate the relation between numerical distance and differences in visual cues.

Analyses

We ran the program 50 times. For each of these 50 runs, a regression analysis was conducted (the dependent variable was numerical distance, and the independent variable was differences in visual properties). The average R 2 and p values are reported for the following visual cues: area extended (convex hull), total surface (the aggregate surface of all dots in one array), density (area extended/total surface), item size (average diameter of the dots presented in one array), and total circumference (circumference of all dots in one array, taken together) were investigated in relation to number. The dependent variable was defined in two ways: (1) as the absolute numerical difference between the two numerosities to be compared (for the priming paradigm), or (2) as the Weber fraction [(largest number – smallest number) / largest number; for the number comparison and habituation paradigms].

Importantly, the area extended is generally defined as the stimulus area (e.g., a circle with a diameter of 10 degrees of visual angle). In such a case, area extended is not necessarily equal to the actual area extended by the dots: Namely, assigning dots to random locations within the stimulus area can lead to clustering of dots in a small part of that area, so that the area extended is smaller than the stimulus area. To overcome this problem, we used the convex hull. This approach also gives a better insight into the problem that for small numerosities, area extended cannot be controlled for without introducing other confounds. Namely, when a single dot is presented, the area extended is the same size as the dot. In this case, the area extended (but also the circumference) can only become larger than the area extended by, for instance, five dots when the size of this single dot exceeds the area extended by the five dots. Thus, the size of the single dot should be increased to extreme proportions. This approach is not desirable, as now a correlation between the difference in dot size and numerical distance will be introduced. Therefore, the only solution to this problem is either not to include relatively small numerosities in a design with relatively large numerical distances or to perform post hoc analyses to show that area extended cannot account for the results obtained.

Results and discussion

Priming paradigm

For the numerosities 1–4, the analyses revealed that density (R 2 = .09, p = .04), surface (R 2 = .04, p = .05), and item size (R 2 < .01, p = .75) could only explain a negligible amount of the variance in numerical distance. As expected, circumference (R 2 = .12, p < .01), and especially area extended (R 2 = .28, p < .01), revealed a relatively large R 2 value. This result indicates that the differences in area extended and circumference were confounded with numerical distance. However, when the numerosities 4–7 were used instead of the numerosities 1–4, the R 2 values for all visual properties were small: area extended (R 2 = .05, p = .05), density (R 2 < .01, p = .78), surface (R 2 = .01, p = .3), item size (R 2 < .01, p = .89), and circumference (R 2 = .03, p = .08).

Number comparison paradigm

The analyses revealed that the differences in area extended (R 2 = .02, p = .13), density (R 2 = .01, p = .17), surface (R 2 = .03, p = .03), item size (R 2 < .01, p = .95), and circumference (R 2 = .08, p < .01) could explain only a small part of the variance in numerical distance.

Habituation paradigm

The analyses revealed that the differences in area extended (R 2 = .04, p = .03), surface (R 2 = .04, p = .02), and circumference (R 2 = .11, p < .01) were significant. However, they all explained a relatively small amount of variance in numerical distance. Item size (R 2 < .01, p = .82) and density (R 2 = .02, p = .13) did not reach significance and also showed small R 2 values.

To summarize, the results revealed that for various designs, the program can generate nonsymbolic number stimuli for which the visual cues can only explain a (very) small portion of the variance in numerical distance. Moreover, the results showed that it is beneficial to be able to calculate the relation between numerosity and visual cues. As expected, when small numerosities were included, a relatively large portion of the variance of numerical distance could be explained by the area extended. This is a problem that cannot be circumvented without introducing other confounds. In our study, this confound was specific for numerosities smaller than 4 and not a weakness of our program, as was shown by the analyses that included only numbers larger than 4.Footnote 3 Here, the same paradigm and numerical distances were used as in the first analyses, with the only change being the range of numerosities included (4–7 instead of 1–4). The results obtained showed that visual cues could only explain the variance in numerical distance to a small extent, indicating that our program is suitable for generating nonsymbolic number stimuli.

Conclusions

In the present study, we presented a program that can generate stimuli for nonsymbolic number studies. It can also give insight into the relation between numerical distance and differences in the visual properties of the stimuli. Throughout the experiment, the differences in the number and visual properties were calculated. Hence, post hoc analyses could be conducted to investigate the relation between the visual cues of the stimuli and the numerical distance or the neural or behavioral results obtained. Overall, the program appears suitable for generating stimuli for studies investigating numerosity processing.