Some do and some don’t? Accounting for variability of individual difference structures

Abstract

A prevailing notion in experimental psychology is that individuals’ performance in a task varies gradually in a continuous fashion. In a Stroop task, for example, the true average effect may be 50 ms with a standard deviation of say 30 ms. In this case, some individuals will have greater effects than 50 ms, some will have smaller, and some are forecasted to have negative effects in sign—they respond faster to incongruent items than to congruent ones! But are there people who have a true negative effect in Stroop or any other task? We highlight three qualitatively different effects: negative effects, null effects, and positive effects. The main goal of this paper is to develop models that allow researchers to explore whether all three are present in a task: Do all individuals show a positive effect? Are there individuals with truly no effect? Are there any individuals with negative effects? We develop a family of Bayesian hierarchical models that capture a variety of these constraints. We apply this approach to Stroop interference experiments and a near-liminal priming experiment where the prime may be below and above threshold for different people. We show that most tasks people are quite alike—for example everyone has positive Stroop effects and nobody fails to Stroop or Stroops negatively. We also show a case that under very specific circumstances, we could entice some people to not Stroop at all.

A prevailing folk wisdom is that different people do things differently; and in psychological science, the study of individual differences has a long and storied tradition (Cattell, 1946). A modern target of inquiry has been to understand the covariation of individuals’ performance in common cognitive tasks that tap perceptual, attention, and mnemonic abilities (e.g., Miyake et al., 2000). In the usual course of studying these relationships, individuals are almost always considered as coming from a continuous, graded distribution, most often the normal (e.g., Bollen, 1989).

Yet, the tasks that researchers study often have a natural zero point. Take for example, a common number-priming task (Naccache & Dehaene, 2001; Pratte & Rouder, 2009). Here, participants are asked to determine whether a target digit is greater than or less than 5. Before participants see the target digit, they are exposed to a briefly flashed prime. This prime is another digit, also greater than or less than 5. The prime may be congruent with the target, i.e., both numbers are less than (greater than) 5, or it may be incongruent with the target, where each has a different status from the number 5. People respond more slowly to targets when the prime is incongruent than congruent, and this slow down defines the priming effect. Note that there is a natural zero point where there is no priming, that is, responses to targets are the same for congruent and incongruent primes. A positive priming effect occurs when responses to targets following congruent primes are faster than those following incongruent primes; a negative priming effect occurs when responses to targets following congruent primes are slower than those following incongruent primes. Here, negative and positive priming effects are qualitatively different because they lead to different theoretical implications. A positive priming effect may indicate the presence of response activation from the prime (Eriksen & Eriksen, 1974). A negative priming effect may indicate temporal segregation and suppression (Dixon & Di Lollo, 1994).

Cognitive psychologists are well aware of the importance of the qualitative and theoretical distinction between positive and negative effects. When experimentalists can find manipulations that switch an effect from positive to negative, the switch itself becomes a target of study. For example, Eimer and Schlaghecken (2002) show a reversal of the priming effect. In their Experiment 2, they manipulate the prime presentation duration. For longer presentation durations, say between 60 and 100 ms, the regular, positive priming effect is observed. For shorter presentation durations, say between 16 and 50 ms, the authors document a negative priming effect. The combination of results is interpreted as evidence for two different priming processes: a subliminal process leading to inhibition, and a supraliminal process leading to facilitation of the primed response. A second example for the reversal of an effect comes from Rouder and King (2003). The authors reversed the usual Eriksen flanker effect by using morphed targets. When targets were morphed between two letters, there was a contrast effect where responses to targets incongruent with their surrounds were speeded. When clear letters were used, there was the typical assimilation effect where responses to incongruent targets were slowed down. Rouder and King (2003) interpreted the combination of results as implicating two separate and opposing effects in perception and response selection.

Although these examples show that it may be possible to reverse specific effects in tightly controlled contexts, doing so remains quite rare. To our knowledge, nobody has reversed the Stroop effect where responses are faster to incongruent items than to congruent ones. Likewise, it is unlikely that a strength effects can be reversed—that is, we doubt, for example, that there are conditions where responses may be quicker to dim lights than to bright ones, and because these phenomena seemingly cannot be reversed, simple explanations are warranted. In the strength case, it may indicate a rather direct link between stimulus strength and neural activation without much opportunity for modulation from top-down processes. We suspect for a wide class of phenomena, the zero point is never crossed (Haaf & Rouder, 2017).

These examples, where zero is crossed and where it is not, show the theoretical importance of the zero point in understanding cognition. Yet, considerations of individual differences, where individuals’ abilities are assumed to come from a graded distribution, do not respect this importance. If an analyst assumes say that individuals’ true Stroop abilities come from a normal distribution, then some people by definition are assumed to have a truly negative Stroop effect. What a fantastic finding that would be! The problem with graded distributions that cross the zero point is that they deny the possibility that true-negative effects do not occur. In doing so, they miss the possibility of important global constraints like the impossibility of negative Stroop effects.¹

Another problem with graded distributions of individuals’ effects is that they explicitly assume that no individual has a true effect of exactly zero.² Yet, the idea that some individuals do not display an effect is compelling from a theoretical point of view. Are there effects where some people are immune, and if so, how could we tell?

The main goal of this paper is to develop models that encompass several configurations of individual variability. Do individuals follow a graded distribution? Are there order-constraints such that nobody can have a negative effect? And are there individuals with truly no effect? The work builds on our previous development where individuals could be all positive, all negative, all null, or follow the traditional graded normal distribution (Haaf & Rouder, 2017; Thiele et al., 2017). None of our previous work, however, captures the notion that “some do and some don’t,” that is that some individuals show a positive effect while others show no effect.

Previously, researchers have attempted to solve this problem with classification: They assume there are do-ers and don’t-ers, and classify people as such. We show next why this approach does not work well. Then we develop our models and apply them to a number of extant context and priming effects. The results are quite surprising—we show that there are cases where “everyone does” and other cases where “some do and some don’t.” We have yet to find a case where some people have a negative effect while others have a positive effect. Perhaps this unicorn is out there, and the tools developed here define the state-of-the-art for finding it.

To understand the nature of the problem and the solution, it is critical to distinguish between observed and true effects. Take, for example, data from a priming task shown in Fig. 1.³ Plotted are each individual’s sample effect—that is, the difference between the mean response for incongruent primes and congruent primes. The sample effects are ordered from smallest to largest in the figure, and as can be seen, some are negative, others are near zero, and a few are substantially positive. However, this does not mean that any particular person has a true effect that is negative, near zero, or positive. True effects are the underlying latent effects we could observe if we had infinitely many trials per individual. They are the target of interest; we wish to know whether they are negative, zero, or positive. The sample effects reflect the true effects, but they are also perturbed by trial noise. Hence, some analysis is needed to infer the qualitative status of the true effects.

Fig. 1

Individual observed effects from a priming task ordered from lowest to highest. Shading of the points indicates the direction of the effect according to two criteria. Dark blue points indicate a positive priming effect for the criterion of BF > 2. Light or dark blue points indicate a positive priming effect for the criterion of 80%CIs excluding zero. White points indicate a null effect according to both criteria

The argument against classification

One approach that has been developed for the problem of capturing individuals’ positive, negative and null effects is classification. An example comes from Fific et al., (2008), who classified individuals as using serial, parallel, or coactive processing based on, among other analyses, the direction and magnitude of an interaction contrast. In their Experiment 1, they conclude that five participants engage in serial processing, two participants engage in parallel processing, and none of the participants engages in coactive processing. We can apply a simple classification approach to the data in Fig. 1 considering each individual’s confidence interval (CI) around their sample effect. The idea is that the true value is likely somewhere in the CI (cf. Morey et al., 2016a, 2016b). The bars show the 80% confidence intervals, and the key observation is whether these CIs include zero or not. We see no individuals are highly likely to have truly negative effects, some may have null effects, and a few others are squarely positive. Of course, we need not use CIs; we can even calculate a Bayes factor per individual, and once again, we conclude that some individuals show a positive effect and some show no effect.

Yet, the approach in Fig. 1 has a flaw—it is prone to overstating the amount of structural diversity across people. Sample noise will make it seem that different people are in different regions of negative, null, and positive. For example, even if everyone was positive, by sample noise we would expect to observe some people as having a negative observed value, others near zero, and still others as having a positive observed value. This critique comes from Lee and Webb (2005) who note that it is important to model the variability across individuals as well as within an individual. The question, then, is what type of model should be used?

For this purpose, Lee and Webb (2005) proposed a non-parametric Bayesian modeling approach similar in spirit to cluster analysis. If there is a natural group structure, individuals are clustered together. The number of clusters, their locations, and their variances are estimated. Lee and Webb’s approach is noteworthy in many respects, but it does not take into account the qualitative distinctions among negative, null, and positive effects. For example, individuals with true effects of − 20 ms and 20 ms may be lumped together while those with true effects of 20 ms and 200 ms may be lumped apart. This is problematic because if individuals truly differ in the sign of effects, a far more complicated and nuanced set of processes is implicated.

To address this issue, Haaf and Rouder (2017) and Thiele et al., (2017) developed an approach based on model comparison. Instead of using a single model, say a clustering-like model used by Lee and Webb (2005), Haaf and Rouder (2017) and Thiele et al., (2017) propose that researchers compare several different models where each model instantiates different possible configurations of individual differences. We extend this approach here to assess the folk wisdom that some do and some don’t. Figure 2 shows different possible configurations of models. Panel A shows a strong null model. All people have a true null effect, and this null effect is indicated by the spike at zero. Panel B shows a common-effect model; all people have the same true positive effect. Panel C shows a case where individuals’ effects vary, but, importantly, they do not cross zero. Moreover, there is no mass at zero, and this model is a flexible version of the “everyone does” position. Panel D shows a model where some do and some don’t show an effect. It is a mixture model, and with a certain probability individuals have no effect. Models of this type are called spike-and-slab models (George and McCulloch, 1993; Mitchell & Beauchamp, 1988), with the spike referencing the point mass at zero and the slab referencing the positive distribution. People who are truly in the spike have no true effect and those who are in the slab have a true effect in the positive direction.

Fig. 2

Models capturing different configurations of individual differences in true effects. a, b A null model and a common-effect model without individual variation. c A model with individual variability where all effects are positive. d A model where some individuals have no effect and others have a positive effect. e A model where some individuals have no effect and others have a positive effect, and again others have a negative effect. f Common random-effects model that captures the case where individuals come from a graded, continuous distribution

Panel E shows a three-component mixture: some people show a true positive effect, some show a true negative effect, and some show a true null effect. This model is again a spike-and-slab model with one spike at zero and two slabs, one on each side of zero. Note that there are only a few cases where this model may be theoretically implied. One such case is Fific et al., (2008), where all three components of the model may be mapped to different processing architectures. Yet, we will not carry this model for the current analysis. One reason is that it is not theoretically useful for the applications chosen here. A second reason is that it is computationally inconvenient (We will return to the computational difficulties in the discussion section). A third, and perhaps most important reason, is that if this case holds, the normal model in Panel F will fare quite well. We show this in simulation subsequently.

Panel F shows the usual case where individuals’ true effects follow a normal distribution. Even though the model has a convenient mathematical form, it does not take the theoretical importance of the zero point into account. It may be used to highlight the differences between conventional approaches and our development.

The goal here is to assess the evidence from the data for the various models in Fig. 2. If models in the top row are favored, then we may favor accounts where each individual is behaving with the same strategies and processes. Alternatively, if models in the bottom row are favored, then we may favor accounts with qualitative differences in processing and strategies among individuals. The approach is different from categorization because the goal is not to categorize individuals but to compare models of configural relations that embed important theoretical distinctions.

From a classical perspective, the analyses of and comparison among the models in Fig. 2 is difficult. The analyst must account for the possible range restrictions on true effects, and doing so is known as order-restricted inference. Order-restricted inference is a difficult topic in statistical analysis (Robertson et al., 1988; Silvapulle and Sen, 2011), and we know of no tests appropriate for the comparison of the null model of Fig. 2a to the “everyone does” model in Fig. 2c. In contrast, Bayesian model comparison through Bayes factors is conceptually straightforward and computationally convenient. Gelfand et al. (1992) provide the conceptual insights; Haaf and Rouder (2017) and Klugkist et al., (2005) provide the computational implementations for all the models except the spike-and-slab versions. The development of the spike-and-slab model that encodes the “some do and some don’t” position is novel. We are proud of the development because the model addresses an important element of folk wisdom, and serves as a precursor for more advances mixture models. Moreover, we are proud to have made the analysis computationally convenient.

In the next section, we provide a brief formal overview of the models depicted in Fig. 2. Following this, we informally outline the Bayes factor model comparison strategy. With the Bayes factors developed, we analyze priming and Stroop interference data. We document at least one case where the some-do-and-some-don’t wisdom seems to be a good description.

Models of constraints

The tasks we consider here have two conditions that can be termed compatible and incompatible, or more generally, control and treatment. It is most convenient to discuss the models in random-variable notation. We start with a basic linear regression model. Let Y_ijk denote the response time (RT) for the ith participant, i = 1, … , I, in the jth condition, j = 1, 2, and the kth trial, k = 1, … , K_ij.⁴ The linear regression model is

$$ Y_{ijk} \sim \text{Normal}(\alpha_{i} + x_{j}\theta_{i}, \sigma^{2}). $$

(1)

Here, α_i is each individual’s true intercept and θ_i is each individual’s true effect. The term x_j is an indicator for the condition, which is zero for compatible trials and one for incompatible trials. The parameter σ² is the variance of repeated trials within a cell. The critical parameters in the model are the true individuals’ effects, θ_i. Placing constraints on these true effect parameters results in the models depicted in Fig. 2.

Null model

The null model is denoted as ₀ and specifies a true effect of zero for all individuals:

$$\begin{array}{llr} \mathcal{M}_{0}: && \theta_{i} = 0. \end{array} $$

This null model is more constraining than the usual null where the average across individuals is zero. Here, in contrast, each individual truly has no effect. An illustration of the model is shown in the first panel in Fig. 3. The figure illustrates the dimensionality of the models for two participants, and it is a guide useful for the following models. Shown are two hypothetical participants’ true effects, θ₁ and θ₂, shown in the figure. For the null model, θ₁ and θ₂ have to be exactly zero. As a result, the density of the distribution of θ_i is a spike at zero, corresponding to the dark point at zero in the figure. The model also corresponds to Fig. 2a.

Fig. 3

Model specification and predictions for two exemplary participants. Left column: Model specifications conditional on specific prior settings. Middle column: Marginal model specifications integrated over prior distributions show correlation between individuals’ effects. Right column: Resulting predictions from each model for data. The red dots show a hypothetical data point that is best predicted by the common-effect model (second row)

Common-effect model

The common-effect model, denoted ₁, corresponds to the spike in Fig. 2b, and it is less constrained than the null. Individuals share a common effect with no individual variability,

$$\begin{array}{llr} \mathcal{M}_{1}: && \theta_{i} = \nu^{+}, \end{array} $$

where ν⁺ denotes a constant, positive effect. The first panel in the second row of Fig. 3 shows that both θ₁ and θ₂ are restricted to the diagonal line, depicting that individual participants’ effects have to be equal. The diagonal is restricted to be positive to ensure that the model only accounts for effects in the expected direction. Every individual has the exact same true effect, but this effect is only restricted to be positive, not fixed to a specific value. The diagonal line results from this a priori uncertainty about the size of the effect.

Positive-effects model

The positive-effects model is denoted ₊, and it is the first model that introduces true individual variability. True individuals’ effects may vary, they are, however, constrained to be positive:

$$\begin{array}{llr} \mathcal{M}_{+}: && \theta_{i} \sim \text{Normal}^{+}(\nu, g_{\theta} \sigma^{2}), \end{array} $$

where Normal⁺ refers to a normal distribution truncated below at zero, ν is the mean parameter for this distribution, and g_θσ² is the variance term. The model is illustrated in the first panel of the third row of Fig. 3.⁵ Both θ₁ and θ₂ are restricted to be positive, but can be different. Values closer to zero are more plausible. The model roughly corresponds to Fig. 2c. In both cases, the distribution on θ_i is restricted to positive values. Yet, the shape in the figure is different from the one for the positive-effects model specified here.

Spike-and-slab model

The spike-and-slab model is denoted _SS. Here, the distribution on θ_i consists of two components, the spike and the slab. Whether an individual’s effect is truly in the slab or in the spike is indicated by the parameter z_i. If an effect is truly null, z_i = 0; if an effect is truly positive z_i = 1. The distribution of θ_i conditional on z_i is

$$\begin{array}{@{}rcl@{}} \mathcal{M}_{SS}: \qquad \begin{array}{l} \theta_{i} | (z_{i} = 1) \sim \text{Normal}^{+}(\nu, g_{\theta} \sigma^{2}),\\ \theta_{i} | (z_{i} = 0) = 0, \end{array} \end{array} $$

Here, the spike corresponds to the null model and the slab corresponds to the positive-effects model. In model specification, every individual has some probability of being in the spike and a complementary probability of being in the slab. The first panel in the fourth row of Fig. 3 shows the model specifications for two participants. For these hypothetical individuals, four combinations of true effects are plausible: 1. Both individuals are in the spike. In this case, θ₁ and θ₂ have to be zero, indicated in the figure by the dark point at (0,0). 2. Both participants are in the slab. θ₁ and θ₂ can take on any positive value, restricting the true effects to the upper right quadrant in the figure, just as with the positive-effects model. 3. θ₁ is in the slab and θ₂ is zero. This case is represented by positive θ₁ values on the horizontal line at y = 0. 4. θ₂ is in the slab and θ₁ is zero. This case is represented by positive θ₂ values on the vertical line at x = 0.

Unconstrained model

The unconstrained model, denoted _u, is the random-effects model in Fig. 2f. Here, a normal distribution without any constraint is placed on the individual’s true effects:

$$\begin{array}{llr} \mathcal{M}_{u}: && \theta_{i} \sim \text{Normal}(\nu, g_{\theta} \sigma^{2}). \end{array} $$

The first panel in the last row of Fig. 3 shows these model specifications. True individuals’ effects can take on any values, and values closer to zero are more plausible. With this model, there is no explicit way of taking differences in the sign of the effect into account. The model serves as a none-of-the-above option capturing when some individuals’ effects are truly negative.

Prior specifications and hierarchical constraints

The five models are analyzed in a Bayesian framework. Bayesian analysis requires a careful specification of prior distributions on parameters. These priors are needed for parameters α_i, the individual intercepts; σ², the variance of responses in each participant-by-condition cell; the collection of z_i, each individual’s indicator of being in the spike or the slab; ν, the mean of effects; and g_θ, the variance of effects in effect-size units. The priors parameters that are common to all models are not of particular concern. They do not affect model comparison, and we follow Haaf and Rouder (2017) in specification.⁶ Several of the models ascribe individual differences across true effects. In this regard, individuals should be treated as random, and a hierarchical treatment is appropriate (Lee, 2011; Rouder & Lu, 2005; Rouder et al., 2008). We model individual differences as coming from either a normal or truncated normal with free mean and variance parameters. Prior settings on these parameters, ν and g_θσ², may affect inference. In the following, we describe the reasons for this influence. We show the effects of reasonable ranges of prior settings on these two parameters in the Discussion section.

The shared mean parameter, ν, induces correlation between the individuals’ effects. Take, for example, the unconstrained model. We can recast the model on θ_i as θ_i = ν + 𝜖_i, where ν remains the population mean and 𝜖_i ∼Normal(0,g_θσ²) is the independent residual variation specific to an individual. The parameter ν is not given. Just as the shared effect in the common-effect model, ν must be estimated. It has variability in this regard and this shared variability induces a correlation between individuals’ effects. We take this variation into account by computing a marginal model on θ_i. The marginal models are shown in the second column of Fig. 3. For the unconstrained model and the other models that specify variability, the correlation is apparent in the figure. This correlation induces dependency between θ_is, and the resultant of this dependency is a reduction in the dimensionality of the models. This reduction makes the unconstrained model, for example, more similar to the common-effect model, which is important for model comparison.

Estimation model

The above five models describe possible constraints on individuals’ effects. Assessing how applicable these models are to data is the core means to determining whether all individuals’ true effects are positive, some individuals’ true effects are null, or some individuals’ true effects are even negative. In the next section, we discuss a formal inferential approach—Bayes factors—for model comparison. Even though model comparison is the main target, estimating parameters and visualizing them remains a tool for understanding structure in data. When constructing an estimation model here, we have two goals: One is to have relatively few constraints on the parameters; the second is to respect the possibility of true null effects. To meet these goals, we place a generalized spike-and-slab model on θ_i.

The model has a spike at zero and a normal distribution as slab. It may be viewed as a mix between panel a and panel e in Fig. 2. The distribution of each individual’s effect, θ_i, is

$$\begin{array}{@{}rcl@{}} \theta_{i} | (z_{i} = 1) &\sim& \text{Normal}(\nu, g_{\theta} \sigma^{2}),\\ \theta_{i} | (z_{i} = 0) &=& 0. \end{array} $$

This spike-and-slab model, just as the unconstrained model in Fig. 2, is agnostic toward the direction of individuals’ effects. It is, however, appropriate for estimating posterior spike and slab probabilities and the collection of θ.

Evidence for constraints

In the previous sections, we develop five models: the null model, the common-effect model, the positive-effects model, the spike-and-slab model, and the unconstrained model that embed various meaningful constraints. Here, we provide a discussion on how to state evidence for these five models in the Bayesian framework. Rather than providing a formal discourse, which may be found in Jeffreys (1961), Kass and Raftery (1995), and Morey et al. (2016a, b), we provide an informal discussion that we have previously presented in Rouder et al., (2016) and Rouder et al. (2018a, b). Informally, evidence for models reflects how well they predict data.

The predictions for data from each of the five models here are shown in the right column of Fig. 3. These predictions are for observed effects, θ̂, for each of the two exemplary participants. Note that predictions are defined on data while model specifications are defined on true effects, and this difference is reflected in the plotted quantities in the figure. For the null model, for example, true effects, left column, have to be exactly zero, and the observed effects, right column, are predicted to be near (0,0). The predictions are affected by sample noise, inasmuch as sample noise smears the form of the model.⁷ The remaining rows of Fig. 3 show the predictions for the common-effect, positive-effects, spike-and-slab, and unconstrained models. In all cases, the predictions are smeared versions of the models.

Once the predictions are known, model comparison is simple. All we need to do is note where the data fall. The red dots in the right column of Fig. 3 denote hypothetical observed participants’ effects. These observed effects, 40 ms for participant 1 and 60 ms for participant 2, are both positive and about equal, and we might suspect that the common-effect model does well. To measure how well, we note the density of the prediction at the observed data point. The densities for the models have numeric values, and we may take the ratio to describe the relative evidence from the data for one model vs. another. For example, the best fitting model in the figure, the common-effect model, has a density that is three times the value of that of the unconstrained model. Hence, the data are predicted three times as accurately under the common effect model than under the unconstrained model. This ratio, 3 to 1, is the Bayes factor, and it serves as the principled measure of evidence for one model compared to another in the Bayesian framework.

Bayes factors are conceptually straightforward—one simply computes the predictive densities at the observed data. Nonetheless, this computation is often inconvenient in practice. It entails the integration of a multidimensional integral, which is often impossible in closed form and may be slow and inaccurate with numeric methods. For the five models here, we follow the development by Haaf and Rouder (2017) using two methods to compute Bayes factors: An analytic approach pioneered by Zellner and Siow (1980) and expanded for ANOVA by Rouder et al., (2012), and the encompassing approach introduced by Klugkist et al., (2005). Figure 4 shows which method is used for which of the models.

Fig. 4

Bayes factor computations for the five models. Bayes factors between the unconstrained, common-effect, and null model can be computed using analytical solutions. Bayes factors between the spike-and-slab model, the unconstrained model, the positive-effects model, and the null model can be computed using the encompassing approach. All other Bayes factors can be computed utilizing the transitivity property of Bayes factors

The encompassing approach is used for Bayes factor computations for the positive-effects model and the spike-and-slab model. The computations for the positive-effects model are detailed in Haaf and Rouder (2017). New to this paper are model comparisons with the spike-and-slab model. Although the spike-and-slab model is precedented and popular, we are unaware of any prior development for comparing it as a whole to alternatives. Our approach is a straightforward application of the encompassing approach. The encompassing approach is a simple counting method within Markov chain Monte Carlo (MCMC) estimation. Take, for example, the Bayes factor between the null model and the spike-and-slab model. The target parameters for the Bayes factor computation are the collection of z_i, the individuals’ indicators of being in the slab. Here we use z to denote the vector of z_i. Using these parameters, the Bayes factor between the null model and the spike-and-slab model can be expressed as

$$B_{0 SS} = \frac{P(\boldsymbol{z} = \boldsymbol{0}|\boldsymbol{Y},\mathcal{M}_{SS})}{P(\boldsymbol{z} = \boldsymbol{0}|\mathcal{M}_{SS})}, $$

where the event z = 0 indicates that every individual is in the spike. This Bayes factor is the posterior probability that all individuals are in the spike relative to the prior probability that all individuals are in the spike. The same approach can be used for comparing the spike-and-slab model to the positive-effects model, using the posterior and prior probabilities that every individual is in the slab.

Using the encompassing approach in MCMC sampling, one can count the number of iterations where z = 0 when z_i are sampled from the posterior; likewise, one can count the number of iterations where all z = 0 when the z_i are sampled from the prior. Let z[m] denote a vector of i samples of z (one for each individual) on the mth iteration under the spike-and-slab model. The mth iteration is considered evidential of the null model if all I elements of z[m] are zero, that is, on this iteration, every individual’s effect θ_i is sampled from the spike. Let n₀₁ be the number of evidential iterations from the posterior, and let n₀₀ be the number of evidential iterations from the prior. Then, the Bayes factor is

$$B_{0 SS} = \frac{n_{01}}{n_{00}}. $$

To compute the Bayes factor of the spike-and-slab model to the remaining models, we use the well-known transitivity of Bayes factors (Rouder & Morey, 2012). Figure 4 provides an illustration for this transitivity: Say the common-effects model predicts the data three times better than the unconstrained model, and the common-effect model predicts the data 20 times better than the null model. We can use these two Bayes factors to calculate the Bayes factor for the unconstrained model over the null model as follows: B_u0 = B₁₀B_1u = 20 3 = 6.67.

Application

We apply the five models to three different data sets: A priming data set provided by Pratte and Rouder (2009), and two Stroop experiments provided by Pratte et al., (2010). The goal here is to answer the question of whether some participants show an effect while others do not. We provide estimation and model comparison results for the three data sets and discuss them in the light of the experimental paradigms.⁸

Priming data set

The priming data used here, reported by Pratte and Rouder (2009), come from a number-priming task where the primes are flashed briefly before the target stimulus is presented.⁹ From our experience with these tasks, we suspect the spike-and-slab model to perform well with some participants being affected by briefly presented primes and others not being affected.

In the task, numbers were presented as primes, followed by target digits that had to be classified as greater or less than five. There is a critical congruent and incongruent condition: The congruent condition is when the prime and the target are both on the same side of five, e.g., the prime is three and the target is four; the incongruent condition is when the prime and the target are opposite, e.g., the prime is eight and the target is four. The priming effect refers to the speed-up in responding to the target in the congruent versus the incongruent condition. Prime presentation was brief by design, and the goal was to bring it near the threshold of detection. Yet, it is well known that this threshold varies considerably across people. For example, Morey et al., (2008) report high variability in individual threshold estimates for prime perception. Other researchers use adaptive methods to change presentation duration individually for each participant until identification of primes is on chance (e.g., Dagenbach, Carr, and Wilhelmsen, 1989). For any given presentation duration, some individuals may be able to detect the prime and others may not. This difference may lead to variability in processing with some people processing the primes and others not.

Results

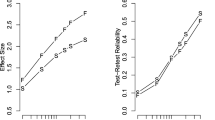
Figure 5a provides two sets of parameter-estimation results. The first set, denoted by the crosses that span from − 0.02 s to 0.03 s, are the observed effects for the individuals, and these are the same points that are plotted in Fig. 1. Observed effects in this context are the differences in individuals’ sample means for the incongruent and congruent conditions. Crosses are colored red or gray to indicate whether the observed effects are negative or positive, respectively. Overall, effects are relatively constrained with no participant having more than a 31-ms effect in absolute value. Estimates from the hierarchical estimation model are shown in blue circles. These estimates are posterior means of θ_i where the averaging is across the spike and slab components. The posterior weights of being in the slab are denoted by the shading of the points with lighter shading corresponding to greater weights. The 95% credible intervals, again across the spike and slab components, are shown by the shaded region.

Fig. 5

Model estimates (left column) and Bayesian model comparison results for (a, b) the priming data set; (c/d) the location Stroop task; e/f the color Stroop task. Left column: Crosses show observed effects with red crosses indicating negative effects. Points show model estimates with lighter shading indicating larger posterior weights of being in the slab. Right column: Bayes factors for all five models. The red frames indicate the winning model

We focus on the contrast between the sample effects and the model-effect estimates. Although the sample effects subtend a small range of about 50 ms, the model-based estimates subtend a much smaller range from almost no effect to an 11-ms effect. These hierarchical estimates reflect the range of true variation after sample noise is accounted for. The compression is known as regularization or shrinkage, and prevents the analyst from overstating evidence for heterogeneity. Hierarchical regularization is an integral part of modern inference (Efron and Morris, 1977; Lehmann & Casella, 1998), and should always be used wherever possible (Davis-Stober et al., submitted). The individuals’ posterior probability of being in the slab ranges from 0.30 to 0.64.

From the model estimates, it is evident that individual effects are tightly clustered and slightly positive with a mean of 4 ms. Yet, these results are not sufficient to answer the question whether “some do and some don’t”. It is unclear whether everyone has a small effect or some people have no effect while others have a slightly larger one. To answer this question we analyze the above models and compare them with Bayes factors. The results are shown in Fig. 5b. The common-effect model is preferred, indicating that everyone has a single, common effect. The next most parsimonious model is the null model, where all individuals have no effect, and it predicts the data about 8.60 times worse than the common-effect model. The Bayes factor between the spike-and-slab model and the common-effect model is 30-to-1 in favor of the common-effect model. We take this Bayes factor as evidence that all do: everybody has a small priming effect.

A location Stroop experiment

Pratte et al., (2010) ran a series of Stroop and Simon interference experiments to assess distributional correlates of these inference effects. As part of their investigations, they constructed stimuli that could be used in either task, and with this goal, they presented the words “LEFT” and “RIGHT” to either the left or right side of the screen. In the Stroop tasks, participants identified the location; in the Simon task, they identified the meaning.

In their first attempt to use these stimuli, Pratte et al., (2010) found a 12-ms average Stroop effect. This effect is rather small compared to known Stroop effects, and was too small for a distributional analysis. To Pratte et al., the experiment was a failure. At the time, Pratte et al. speculated that participants did not need to read the word to assess the location. They could respond without even moving their eyes from fixation, and even though reading might be automatic at fixation, it may not be in the periphery. To encourage participants to read the word, Pratte et al. subsequently added a few catch trials. On these catch trials, the word “STOP” was displayed as the stimulus to the left or right of fixation, and participants had to withhold their response. This manipulation resulted in much larger Stroop effects.

Here we analyze data from the failed experiment where there was a small Stroop effect of 12 ms (Experiment 2 from Pratte et al., 2010). Our question is whether some participants shift their attention to the word in the periphery while others do not. In this scenario, we would find that the spike-and-slab model would perform well. The alternative is that all participants exhibited a small Stroop effect similar to the priming effect above.

Results

Observed effects are shown by the crosses in Fig. 5c. Of the 38 participants, ten show an observed negative Stroop effect, shown by red crosses in the figure. The average effect is 11.90 ms with individuals’ effects ranging from − 19 ms to 68 ms.

Estimates from the hierarchical estimation model are shown in blue circles, and 95% credible intervals are shown by the shaded region. Again, hierarchical shrinkage is large, reducing the range from 87 ms for observed effects to 45 ms for the model estimates. Of note is also that the individuals’ posterior probability of being in the slab varies considerably, ranging from 0.20 to 0.99. This difference in posterior weight suggests that some individuals are better described by the spike while others are almost definitively in the slab.

The model comparison results in Fig. 5d confirm this consideration: the Bayes factor between the spike-and-slab model and the runner-up common-effect model is 3.50-to-1 in favor of the spike-and-slab model. This Bayes factor provides slight evidence for the “some do and some don’t” wisdom in this particular Stroop experiment.

A color Stroop experiment

Pratte et al., (2010) ran another experiment, a more standard Stroop task with color terms (Experiment 1 from Pratte et al., 2010). For this experiment, in contrast to the failed Stroop experiment, we expected that everyone shows a positive Stroop effect.

Results

Parameter estimates are shown in Fig. 5e. Individuals’ observed effects are fairly large with an average of 91 ms with only one participant showing an observed negative effect. There is less shrinkage than for the other data sets. The range for the observed effects is 221 ms; the range for the hierarchical estimates is 144 ms. Posterior probabilities of being in the slab are high with only one person having a lower probability than .85.

The model comparison results are shown in Fig. 5f. Overall, there is the most evidence for the positive-effects model. The second-best model is the unconstrained model. The Bayes factor between these two models is 8-to-1 in favor of the positive-effects model, and this Bayes factor can be interpreted as evidence that all do. The spike-and-slab model fares even worse with a Bayes factor of 1-to-23 compared to the positive-effects model. The results suggest that everyone shows the expected Stroop effect—if targets are presented at fixation.

Concerns

The Bayesian modeling approach developed here requires judicious choices in model and prior specification. An attentive reader may have some concerns about our choices. It is reasonable to inquire about alternative models that were not included for analysis here; specifications of the normal and truncated normal; sensitivity of the results to prior settings; and computational convenience of the approach. We take these concerns in turn.

Alternative models

The five models developed here are designed to capture the following theoretical positions: 1. No person may have a true effect whatsoever; 2. Everyone has the same positive true effect; 3. Individuals’ effects vary, but everyone has a positive effect; 4. Some people show a true positive effect while others truly show no effect at all; and 5. Individuals’ effects follow a normal, graded distribution where some people can have a true negative effect. These five, of course, are not the only choices. Here we discuss alternatives.

One area of potential concern is the unconstrained model. Here we use a graded normal, and this is our only specification accounting for the possibility that some people have truly positive effects while others have truly negative effects. There are other model instantiations, however, that capture this state of affairs. One useful alternative is the mixture model shown in Fig. 2e. Here, there are three groups of individuals: those that are positive, those that are negative, and those that are null. Another possible model is one with two slabs but no spike. If we are willing to speculate, we can come up with a variety of models that instantiate positive and negative effects.

Rather than implementing all of these possible alternatives, we decided to simulate how well our unconstrained normal model fared when the data followed these mixture alternatives. Figure 6a shows the normal model and two alternatives: a two-slab mixture model (labeled “Mixture 1”), and a spike-and-two-slab mixture model (labeled “Mixture 2”). Our aim in choosing particulars for these truths was to equate the overall mean and variance. The true individuals’ effects for each study were the ticks at the top of the panel. We simulated data from these true effects 100 times for each of the three models. The Bayes factor between the normal unconstrained model and the positive model is computed for each of the simulated data sets. The Bayes factor distributions from the simulation are shown in the violin plots of Fig. 6b. The unconstrained model is favored as frequently for the mixture truths as for the normal truth.

Fig. 6

Simulation from three different true models. a True unconstrained models. The red line shows a normal unconstrained model, the blue line shows a mixture model of true negative and true positive effects. The green line shows a mixture of true negative, null, and positive effects. The ticks at the top of the panel show true study effects chosen for simulation. b Resulting Bayes factor distributions for the unconstrained model vs. the positive-effects model for the simulation study. The unconstrained model is preferred most of the time for all three true models

The critical point to emerge from this simulation study is that the unconstrained normal model is a useful instantiation of the unconstrained position, even when misspecified. Here is why: The goal is to detect a few negative true effects against a background of many true positive ones. The normal for this configuration would have a positive mean and sufficient variance so that there is noticeable negative mass (as in Fig. 6a). The distribution of the negative part is not only small in mass, but is skewed such that small negative effects are weighted. The normal therefore is well-suited to detect the most difficult case—the one where negative effects are few and more likely to be clustered near zero. Moreover, with the little negative mass that we expect in these cases, there is little to distinguish a mixture model from the unconstrained.

Another area of potential concern are the point-mass specifications for the null model, the common-effect model and the spike in the spike-and-slab model. Alternative specifications are not just limited to mixture models. A recent trend is to use small equivalence regions instead of point mass (Kruschke and Liddell, 2017; Rogers et al., 1993). Those researchers who are convinced these are helpful models are free to use them, and the Bayes-Factor computations are no challenge (Morey & Rouder, 2011). We do not recommend these models because they provide for less theoretical clarity than either point-mass models or distribution models. The point null, in contrast, is theoretically constrained and useful. This argument is made by Gallistel (2009), Jeffreys (1961), Rouder et al., (2016), and Rouder and Morey (2012), just to name a few.

Normal specification

Another concern with the proposed approach is the reliance on normal parametric model specifications. The advantage of the normal specification is computational convenience. With this specification, the many dimensions of the high-dimension integrals that define the Bayes factor may be computed symbolically to high precision. Without this specification, we suspect numeric integration would be exceedingly slow and inaccurate. Yet, researchers may be concerned about the misspecification of the normal. We focus here on applications with response times, and RTs are skewed rather than symmetric. Moreover, the standard deviation tends to increase with the mean (Luce, 1986; Rouder et al., 2010; Wagenmakers & Brown, 2007).

We think the concern about the normal specification is misplaced. The main reason is that we focus on the analysis of ordinal relations among true means. If we knew individual’s true means, then we could answer questions about the direction of the effects without any consideration the true shapes or true variances. The inference therefore inherently has all the robustness of ANOVA or regression, which is highly robust for skewed distributions, so long as the left tail is thin. Indeed, RTs tend to have thin left tails that fall off no slower than an exponential (Burbeck & Luce, 1982; Van Zandt, 2000; Wenger & Gibson, 2004).

Thiele et al., (2017) addressed this concern through simulation. They considered highly similar models and performed inference with similarly computed Bayes factors. In a simulation, they generated data from a shifted log normal with realistic skewness and with means and variances that varied across individuals and the manipulation. As expected, they found exceptional robustness, and the reason is clear. The main inferential logic is dependent only on true means, and the normal is a perfectly fine model for assessing this quantity even when the data are not normally distributed.

Prior sensitivity

Another concern, perhaps a more pressing concern in our view, is understanding the role and effects of the priors on inference. In general, Bayesian models require a careful choice of priors. These priors have an effect on inference as noted by many Bayesians. A general idea in research is that, if two researchers run the same experiment and obtain the same data, they should reach the same if not similar conclusions. Yet, the priors may be chosen differently by different researchers, and this choice may lead to differing conclusions. To harmonize Bayesian inference with the idea of similar conclusions, many Bayesian analysts actively seek to minimize the effects by picking likelihoods, prior parametric forms, and heuristic methods of inference so that variation in prior settings have marginal effects (Aitkin, 1991; Gelman et al., 2004; Kruschke, 2012; Spiegelhalter et al., 2002). In contrast, Rouder et al., (2016) argue that the goal of analysis is to add value by searching for theoretically meaningful structure in data. Vanpaemel (2010) and Vanpaemel and Lee (2012) argue that the prior is where theoretically important constraints are encoded in the model. In our case, the prior provides the critical constraint on the relations among individuals. We think it is best to avoid judgments that Bayes factor model comparisons depend too little or too much on priors. They depend on it to the degree they do.

Here we focus on understanding the dependence of Bayes factors on a reasonable range of prior settings and the resulting diversity of opinions. Indeed, Haaf and Rouder (2017) took this tactic in understanding the diversity of results with all the models except for the spike-and-slab-model which was not developed at the time. Here we use a similar range of prior settings to understand the dependency on these settings.

The critical prior settings for understanding the diversity of conclusions come from the priors on ν and 𝜖_i (or g_θ). Although they are not the primary target of inference, the prior settings on these parameters do affect Bayes factor results. A full discussion of the prior structures on these parameters is provided in Haaf and Rouder (2017), and here we review the main issues. The critical settings are the scales on ν and 𝜖_i. These scale settings are relative to σ, the residual noise. Our considerations for these scale settings go as follows: In tasks like this, with sub-second RTs, a standard deviation of repeated response times for a given participant and a given condition may be about 300 ms, and we can use this value to help set the scales. For example, for priming and Stroop tasks, we may expect an overall effect of 50ms, and the scale on ν might be 50ms/300ms, or 1/6th of the residual noise. Likewise, if the take the variability of individuals’ effects depicted by 𝜖_i, we may expect this variation to be about 30 ms, or 1/10 of the residual noise.

With these reasonable ranges of variation, we are ready to explore the effects of prior specification on Bayes factors. We explore the effects of halving and doubling these settings, which represents a reasonable range of variation. The results are shown in Table 1. There is a fair amount of variability in Bayes factors, and in our opinion, there should be. The range of settings define quite different models with quite different predictions. Nonetheless, there is a fair amount of consistency. For the priming data, the common-effect model is preferred for all settings, with the null-model and the spike-and-slab models as the next contenders. For the color Stroop data, the positive-effects model is preferred for all settings, and the ordering for the remaining models stays relatively constant. The only data set where the preferred model varies with prior settings is the location Stroop data: The spike-and-slab model is preferred for the chosen settings and when the scale on ν is halved. These settings indicate that small average effects are expected for all models. When the scale on ν is doubled, i.e., larger, about 100 ms effects are expected, the Bayes factor between the common-effect model and the spike-and-slab model is about 1, indicating that none of the two models is preferred over the other. This Bayes factor, however, was not large from the beginning, only about 3-to-1 in favor of the spike-and-slab model. This example illustrates how useful this type of sensitivity analysis can be to understand the range of conclusions that may be drawn from the data. In this case, the evidence for the spike-and-slab model is small, and largely dependent on prior settings. For a convincing result, more evidence for a mixture of effects would be needed.

Table 1 Sensitivity of Bayes factors to prior settings

Computational issues

In previous work we developed the null, common-effect, positive-effects and unconstrained models (Haaf & Rouder, 2017; Thiele et al., 2017). Here we add the spike-and-slab model to capture the folk-wisdom that some do and some don’t show an effect. We show it is a worthy competitor in at least one application. The former four models are computationally convenient both in estimation and in Bayes factor computations. As shown in Fig. 4, Bayes factors can be computed quickly using a combination of Rouder et al.“s (2012) symbolic integration as implemented in the BayesFactor package for R (Morey & Rouder, 2015) and Klugkist and colleagues” encompassing approach (e.g., Klugkist and Hoijtink, 2007).

Computational convenience for the spike-and-slab model is more nuanced. Estimation of this model is quick and stable. The computation of the Bayes factors for the spike-and-slab model, however, is more difficult. The difficulty here is that Bayes factor computation relies on the estimation of each individual’s spike indicator, z_i. This collection of parameters is estimated using Markov chain Monte Carlo methods. For each iteration in the chain, we note that z_i[m] is either zero or one, indicating that the ith persons’ effect is either in the spike or in the slab, respectively. Bayes factor estimation is difficult whenever the majority of the individuals’ effects are in the spike or in the slab. For example, most individuals’ effects in the color Stroop task are estimated to come from the slab distribution. In this case, the critical event is when all z_i are zero, and this event is rare. Hence, it is necessary to run long chains to guarantee enough rare events to estimate its rate of occurrence.

The good news here is that we can assess the accuracy of the Bayes factor estimation for the spike-and-slab model by leveraging the transitivity of Bayes factors. Figure 4 illustrates this check. We can compute the Bayes factor between the unconstrained model and the null model either with the encompassing approach using the spike-and-slab model (Rouder, Haaf, and Vandekerckhove, 2018), or directly with symbolic integration methods (Rouder et al., 2012). We find comparable results from both methods with between 50000 and 100000 iterations in the MCMC chain, indicating good estimations of rates of rare events. Analyzing all five models takes about 45 min on one data set.

Discussion

In this paper, we address the question whether some people show a positive effect, others show a negative effect, and again others show no effect. The example we use here is priming, and we trichotomize the outcome into three basic relations: responses to congruent targets are faster than to incongruent ones (positive effects), responses to congruent targets are slower than to incongruent ones (negative effects), and responses to congruent targets are equally fast as to incongruent ones (no effects). Whether the natural zero point is crossed or not has many theoretical implications. Obvious applications of our approach include context effects (e.g., Stroop, Eriksen, Simon etc.) and strength effects (e.g., stimulus strength, mnemonic strength, etc.).

The approach we take here is Bayesian model comparison across five models: a null model, a common effect model, a positive-effects model, a spike-and-slab model, and an unconstrained normal model. The novel element here is the usage of the spike-and-slab model. Although spike-and-slab models are frequently used in statistics, their most common application is to categorize which covariates (people in our case) are in the spike and which are in the slab. Our usage is novel—we ask how well this spike-and-slab structure predicts the data relative to other models.

Several psychologists have previously asked the related question of whether mixtures account for data. In cognitive psychology, the most common application is whether responses on trials are mixtures of two bases. Falmagne (1968) was perhaps the earliest to formally explore this notion. He asked whether response times for a given individual are the mixture of a stimulus-driven process and a guessing process. Indeed, this type of query has been explored in a number of domains (e.g., Klauer and Kellen, 2010; Province and Rouder, 2012; Yantis, Meyer, and Smith, 1991).

Our approach differs markedly from these previous queries. Our focus is not on characterizing trial-by-trial variability but on characterizing variability across individuals. We do not make as detailed commitments to specific cognitive architectures, but provide a general approach based on ordinal relations of less-than, same-as, and greater-than. In this regard, our approach is more similar to latent class models used in structural equation modeling (Skrondal and Rabe-Hesketh, 2004). In these models, vectors of outcome measures are assumed to come from the mixture of latent classes of people, and the goal is to identify the classes and categorize people into these classes (see also Lee and Webb 2005; Navarro et al., 2006). One critique of this approach is that the models are so weakly identified that it is difficult to reliably recover class structure (Bauer & Curran, 2003). We avoid this problem by restriction. We restrict our classes into three that are well defined as the sign of the outcome measure. In summary, while our approach is similar in some regards to previous latent-class modeling, the statistical development is novel in critical ways.

We apply this approach to three exemplary data sets and find, at least for one case, some support for the claim that some individuals show an effect while others do not. We think, however, these mixtures are relatively rare in cognitive psychology where experimental paradigms tend to isolate the cognitive processes of interest. Only in cases where this isolation is not successful mixtures may occur. This was the case in our location Stroop example, where participants were able to avoid reading the target words by fixating the center of the screen.

If such a mixture occurs, then this result licenses more complicated inquiries. The mixture implies that there are classes of people that have qualitatively different behavior. Why? There are many possibilities including demand characteristics (perhaps some people did not understand the task), strategies, and pathologies. For example, Parkinson patients fail to display foreperiod effects (Jurkowski et al., 2005). We think that once a mixture is documented, the next logical step is to explore person-level covariates—are there any performance, personality, or other covariates that correlate well with whether a person has high probability of being in a particular component of the mixture? Depending on the substantive domain, the presence of mixtures licenses an exploration for rich patterns and structure in data.

In many cases, modeling approaches can be localized on a continuum of applicability: On the one end of the spectrum, models are widely applicable, but they only coarsely test theories. An example for this end would be ANOVA or t tests. On the other end of the spectrum, models are custom tailored to measure specific processes in specific tasks. Our approach is in the sweet spot between these extremes. It is widely applicable in cognitive psychology where priming and strength tasks are prominent, and it addresses a question more complex than “is there an effect” without making a detailed commitment to specific processes. Knowing whether all do or “some do and some don’t” remains timely and topical in perception, action, attention and memory.