A Bayesian approach to mitigation of publication bias

Abstract

The reliability of published research findings in psychology has been a topic of rising concern. Publication bias, or treating positive findings differently from negative findings, is a contributing factor to this “crisis of confidence,” in that it likely inflates the number of false-positive effects in the literature. We demonstrate a Bayesian model averaging approach that takes into account the possibility of publication bias and allows for a better estimate of true underlying effect size. Accounting for the possibility of bias leads to a more conservative interpretation of published studies as well as meta-analyses. We provide mathematical details of the method and examples.

Introduction

It is reasonably well established that publication bias—a differential publishing rate between positive and negative results—permeates the scientific literature (Franco, Malhotra, & Simonovits, 2014). Some of the strongest such claims are made by Ioannidis (2005), who famously concluded that “most claimed research findings are false” (p. 696). Decades earlier, Rosenthal (1979) had pointed out the theoretical possibility that all research findings are false, and that file drawers around the world conceal the 95 % of studies whose luck of the draw did not lead to publication. The prevalence of publication bias has been a growing concern in psychology, especially in recent years, and is often mentioned as one of the causes of the “crisis of confidence” (Pashler and Wagenmakers, 2012). As Young, Ioannidis, and Al-Ubaydli (2008) point out, “the small proportion of results chosen for publication are unrepresentative of scientists’ repeated samplings of the real world” (p. 1418) It is no wonder, then, that successful replication attempts are scarce (e.g., Francis, 2012a).

The favorable results preferred by systemic publication bias are often defined by statistical significance. Results are said to be ‘significant’ if the probability p of observing data that are at least as extreme as the observed is smaller than some criterion α if the null hypothesis is true. The conventional criterion (for psychological scientists) in null hypothesis significance testing (NHST), α = .05, sets a convenient bar for consideration by researchers and reviewers alike. However, the presence of an arbitrary threshold may contribute to the number of positive findings reported in the literature. Masicampo and Lalande (2012) surveyed the distributions of p values in three prominent psychological journals and found that p values were conspicuously more common than expected just below α.

To tackle this important and widespread issue of publication bias, the field can endeavor to prevent future cases, as well as take action to alleviate the current state of psychological science. Our focus is on the latter goal of mitigation, by postulating a set of possible bias mechanisms and using these to improve the estimation of effect sizes in the presumed presence of publication bias.

The idea of publication bias detection is not new—there exist tests for it in the literature (e.g., the test for “excess significance” based on Ioannidis & Trikalinos, 2007), and these have been applied on numerous occasions (e.g., Francis 2012a, b, c). Neither are we the first to propose behavioral models of the publication process (Givens, Smith, & Tweedie, 1997; Greenwald, 1975; Hedges, 1992), and there are several recently developed approaches to deal with publication bias.

One such new method, based on the p-curve, is due to Simonsohn, Nelson, and Simmons (2014). The p-curve is the distribution of statistically significant p values for a set of independent findings. The exact shape of the p-curve is used to determine the evidential value of that particular set of findings, or the set’s ability to rule out selective reporting as the sole explanation of those findings. The central intuition is that if the null hypothesis is true,¹ p-curves are expected to be uniform, but if the null is false, only right-skewed p-curves with more low than high significant p values are diagnostic of evidential values. The p-curve method assesses if the observed p distribution is significantly right-skewed. Inference from p-curve is analogous to null hypothesis significance testing; a right-skewed p-curve does not imply all studies have evidential value, similar to how significance does not imply all observations were influenced by the experimental manipulation. Therefore, the p-curve can only determine whether selective reporting can be ruled out as an explanation for a set of significant findings and cannot make conclusions about estimates of the true underlying population effect size.

Stanley and Doucouliagos (2013) propose another approach consisting of a set of meta-regression approximations that are designed to be a practical solution to the publication bias issue. This method is developed from Taylor polynomial approximations to the conditional mean of a truncated distribution, because results are selected to be statistically significant in the desirable direction. The observed effects will consequently depend on the population’s true effect, plus another term that reflects selection bias. A critical limitation of this method is that it requires a relatively large number of estimates on the same empirical phenomenon because they are based on regression analysis.

Lastly, p-uniform (van Assen, van Aert, & Wicherts, 2014) is again based on the distribution of p values conditional on a certain population effect size μ. For example, if the true population effect size is zero, then the conditional p value distribution should be close to the uniform distribution. Therefore, p-uniform tests the null hypothesis by testing whether the observed conditional p value distribution deviates from the uniform. This method performs three tasks simultaneously: (a) the testing of publication bias; (b) effect size estimation, and (c) the testing of the null hypothesis of no effect. p-uniform only considers studies that report statistically significant results, so those containing non-significant effects are discarded. p-uniform makes two assumptions: (1) homogeneity of population effect size across all studies and (2) that all studies with statistically significant results are equally likely to be published and included in the meta-analysis. According to the authors, p-uniform is the first method to possess the aforementioned three qualities, without making sophisticated assumptions or choices.

Our proposed Bayesian mitigation method encompasses these characteristics as well, in addition to being a Bayesian approach to detect and mitigate the effects of publication bias in the field. We believe we are the first to attempt mitigation of publication bias by—as we will demonstrate—averaging over a set of plausible behavioral models. Our interest is foremost in recovering the true underlying effect size as accurately as possible, and not necessarily to decide whether a particular field exhibits more or less publication bias.

Behavioral models for publication bias

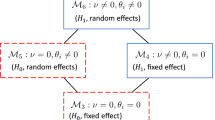
We postulate a set of four generative behavioral models for the publication process. While this set is not exhaustive, we believe it covers a reasonably large range of possible processes. The first model is a no-bias model under which all results, regardless of statistical significance, are published. This would be the optimal scenario for the scientific literature, but it is unlikely to hold in all cases. The second model is an extreme-bias model in which nonsignificant results are never published. The presence of occasional nonsignificant results in the literature implies that this model cannot hold in all cases either. The third model is one inspired by Greenwald (1975), in which nonsignificant results are published with some constant (but unknown) probability. Finally, the fourth model is one inspired by Givens et al. (1997), in which the publication probability is an exponentially decreasing function of the p value if p > α (i.e., it diminishes as the observed p value departs from α = .05).²

For each of the four models, we consider two possible states of nature: either (a) there exists a true effect of some unknown magnitude; or (b) the true effect size is 0. While the behavioral processes are conveniently described through a censoring function that operates on the p value, the state-of-nature component of these models depends on the specific experiment to which our method is applied (i.e., it depends on whether the experiment is comparing two means with a t or a z test, or interactions with an F or a χ ² test, etc.). Each of these models has, as a parameter, the size of the experimental effect, and fitting these models to the observed data (i.e., the reported effect size) will yield a new estimate of the effect size conditional on the censoring process.

The general formulation of the likelihood function associated with these models is:

$$\begin{array}{rcl} p\left( \delta^{obs}\left|\eta^{true}\right., \mathcal{M}, {\Theta}\right) &\propto& p\left( \delta^{obs}\left|\eta^{true}\right.\right)C_{\mathcal{M}}\left( \delta^{obs},{\Theta}\right), \end{array} $$

where δ ^obs is an observed test statistic, η ^true is the true effect size (which may be 0 for some models), and $C_{\mathcal {M}}$ is a model-specific censoring function that describes the probability of an observation of size δ ^obs being published, given the parameters Θ of the censoring process. Figure 1 summarizes the eight models, and a comprehensive mathematical treatment of the models is given in Appendix A. Models of this form are known in the statistical literature as selection models (e.g., Bayarri & DeGroot, 1987, 1991, Iyengar & Greenhouse, 1988).

Fig. 1

Predictions made by the eight proposed models. Left column: the censoring functions for each of the four biasing processes, with on the horizontal axis the observed p value and on the vertical axis the probability of publication P _{p u b} . Middle and right column: the resulting truncated central (center) and noncentral (right) t distributions after applying the censoring functions. The top row is the no-bias model, where the resulting t distributions are simply the central and noncentral t distributions untouched. For the remaining three rows, the t distributions are truncated to the region of significance or downweighted in the complementary region, as determined by the corresponding biasing functions. The figure illustrates that each behavioral model generates t distributions with a unique shape

Bayesian model averaging

A critical issue is that, while we may define any number of behavioral processes that censor the published literature, we do not know which process, if any, was in play for a given report. However, there exist standard statistical tools for dealing with the unknown. The most common such tool is marginalizing over (a.k.a., “integrating out”) an unknown:

$$\begin{array}{rcl} p\left( \eta^{true}\left|\delta^{obs}\right.\right) &=& \sum p\left( \eta^{true}\left|\mathcal{M},\delta^{obs}\right.\right)P\left( \mathcal{M}\left|\delta^{obs}\right.\right),\end{array} $$

where $p\left (\eta ^{true}\left |\mathcal {M},\delta ^{obs}\right .\right )$ is the posterior distribution of the effect size under a censoring process $\mathcal {M}$ and given the observed test statistic δ ^obs. $P\left (\mathcal {M}\left |\delta ^{obs}\right .\right )$ is the probability that $\mathcal {M}$ happened given the observed data. Crucially, we treat the identity of the censoring process $\mathcal {M}$ as merely another unknown and compute the likelihood of each possible value for η ^true using the probability of each model’s truth as a weight (equivalently, we can compute the posterior distribution of a mitigated test statistic δ ^mit as a simple transformation of η ^true). Computing those weights—the posterior probabilities—for each model relies on the same principle, combined with Bayes’ theorem: $P\left (\mathcal {M}\left |\delta ^{obs}\right .\right ) = p\left (\delta ^{obs}\left |\mathcal {M}\right .\right )P\left (\mathcal {M}\right )/p\left (\delta ^{obs}\right )$. p(δ ^obs), in turn, is obtained through marginalization: $p\left (\delta ^{obs}\right ) = \sum p\left (\delta ^{obs}\left |\mathcal {M}\right .\right )P\left (\mathcal {M}\right )$.

Taken together, this yields the posterior distribution of δ ^mit given δ ^obs, which we may then use to make inferences about the existence or non-existence of an effect. In particular, we can now quantify the degree to which the observation δ ^obs changes how likely we consider it that the true effect size is 0. The degree of change from prior to posterior information is known as the Bayes factor, and integrating over models in this way is commonly referred to as Bayesian model averaging (for an introduction, see Hoeting, Madigan, Raftery, & Volinsky, 1999).

Finally, in the case of multiple independent studies s = 1,…,S, and hence a set of multiple observed test statistics $\left \{\delta ^{obs}_{s}\right \}_{s=1}^{S}$, we can compute an aggregated posterior distribution $p\left (\delta ^{mit}\left |\left \{\delta ^{obs}_{s}\right \}_{s=1}^{S}\right .\right )$. The details of this computation are in Appendix B.

Simulation studies

To demonstrate the effects of statistical mitigation, we performed a series of Monte Carlo studies, of which we report four. All studies were based on 500 simulations of each case.

(1) Single result re-analysis

In this Monte Carlo study, we simulated a single empirical result regarding some hypothetical phenomenon of a given effect size. In the simulation, the true effect size ranged from 0 (no effect) to 0.3 (a large effect) in increments of 0.05. The result of a one-sided paired t test (for positive effects) was then either “published” or not, with the publication decision based on one of three regimes: Either the finding was subjected to no publication bias at all (“no bias”), or was subjected to extreme publication bias (“only bias”; only significant effects published), or to a combination of all four censoring functions (with equal probability; “mixture”). This implies that oftentimes no result was published, so there was nothing to compute. In the cases where a result was published, we applied our mitigation method to improve the estimate of the underlying effect size. In addition to the three biasing regimes, we also manipulated the simulated sample size n, which was either small (n = 20), medium (n = 60), or large (n = 150). These values were inspired by Marszalek, Barber, Kohlhart, and Holmes (2011)’s review of typical sample sizes in experimental psychology.

Each panel in Fig. 2 represents one regime × sample size combination, with the horizontal axis indicating the true value of the effect size and the vertical axis representing the estimated effect size. Squares indicate our mitigated effect size, diamonds indicate the classical effect size measure Hedges’ g (also computed in each case on the basis of a single “published” effect size). Unbiased estimates fall on the indicated diagonal.

Fig. 2

Recovery of the mitigation method (squares) for a single paper, evaluated under three different bias conditions, with three different sample sizes, and a range of effect sizes. The classical effect size measure Hedges’ g (diamonds) is given for comparison. Vertical lines extend one standard deviation in each direction. In almost all scenarios, the mitigation method either outperforms the classical method, or recovers the same effect size

In almost all cases, the mitigated effect size is closer to the true effect size than the classical estimator. As the degree of publication bias increases, both measures perform worse, but the effect of publication bias on the classical estimator is dramatic while the effect on the new estimator is comparatively modest. Both methods converge to the true value as the sample size n in the simulated papers increases,³ and in the no-bias scenario Hedges’ g is exact (on average).

(2) Meta-analysis

In the second Monte Carlo study, we simulated a situation in which ten independent studies were conducted on the same hypothetical phenomenon of a given effect size. Again, our effect sizes ranged from 0 to 0.3 in increments of 0.05. For each of the ten studies, the result of a one-sided paired t test was either published or not, under the same three regimes as above, so that some proportion of the results was visible in the literature. We also again manipulated the simulated sample size n, which was either small (n = 20), medium (n = 60), or large (n = 150), and which was the same for all studies in each set. The “unpublished” results were discarded, and meta-analytic effect sizes computed, either using our new method, or using the aggregated Hedges’ g.

Figure 3 is set up in the same way as Fig. 2, with each panel representing one regime ×sample size combination; horizontal axes indicating the true value of the effect size and vertical axes representing the estimated effect size; squares indicate our mitigated effect size and diamonds indicate the classical aggregated effect size Hedges’ g (also computed only on the basis of the “published” effect sizes).

Fig. 3

Recovery of the mitigation method (squares) for a simulated literature of ten papers, of which only a biased subset is visible to the method, evaluated under three different bias conditions, with three different sample sizes, and a range of effect sizes. The classical effect size measure Hedges’ g (diamonds) is given for comparison. In almost all scenarios, the mitigation method either outperforms the classical method or recovers the same effect size

It is again true that in almost all cases, the mitigated effect size is closer to the true effect size, and that the effect of increasing publication bias is greater for the classical estimator than for the new estimator.

(3,4) Meta-analysis with different priors

The final two Monte Carlo studies served to illustrate the sensitivity of our analyses to the prior distribution over models. For this purpose, we repeated the meta-analytical design of the second Monte Carlo study with two alternative prior distributions. Our default prior was (20, 20, 1, 1, 1, 1, 1, 1)/46 (see Appendix B for a rationale), but in these simulations we changed it first to (20, 0, 1, 0, 1, 0, 1, 0)/23, eliminating the null hypothesis, and then to (0, 0, 0, 0, 1, 1, 1, 1)/4, eliminating all but the two more nuanced biasing processes. The qualitative effect of these changes on the recovery performance was negligible, and we do not discuss them here.

Example applications

Wishful seeing

We now consider a single test within a published paper. Balcetis and Dunning (2010) reported evidence for “wishful seeing,” a phenomenon in which desirable objects are perceived to be physically closer than other objects that are less desirable. This effect, the authors suggest, serves the function of energizing the perceiver to engage in actions that lead to the goal of obtaining the desirable object. In one study, participants were asked to position themselves at a certain distance relative to an object. The authors hypothesized that participants would stand further from a desirable object (chocolates) than from an undesirable one (feces), because desirable chocolate would be misperceived as physically closer. In line with their prediction, the authors found a significant effect on perceived distance depending on whether participants saw chocolates or feces (unpaired t ₅₀ = 2.29, p = .026, Hedges’ g = 0.64).

Using only the reported t value and sample size, and making no assumptions beyond those requisite for the t test and a prior on effect size Hedges’ $g = t \sqrt {(n_{f} + n_{c}) / (n_{f} n_{c})}$, we are able to compute probabilities for each of the eight models (using formulas given in Appendix B). These probabilities can then be used as weights to compute a new, mitigated effect size (or, equivalently, t value) that takes into account the possibility and likelihood of biasing mechanisms.

The result of this exercise is displayed in Fig. 4. The left panel depicts prior (grey bars; see Appendix B for a rationale of the choice of prior model probabilities) and posterior (black bars) probabilities of the eight models. The largest change in probability from prior to posterior is seen in model $\mathcal {M}_{2-}$: the extreme-bias model under the assumption that the null hypothesis is true becomes almost eight times more likely after taking into account the data. Model $\mathcal {M}_{1+}$, the model of no bias with the null hypothesis being false, received the highest weight. The panel shows no compelling reason to prefer the two more complex biasing processes $\mathcal {M}_{3}$ and $\mathcal {M}_{4}$.

Fig. 4

Model results for the “wishful seeing” example. Left panel: Prior and posterior probabilities over models. Numbers in the horizontal axis labels indicate the model, + and − indicate the states of nature (true effect vs. no true effect, resp.). Above the bars we indicate the posterior ratio between the two states of nature within each biasing model. For example, if we assume there is no bias at all (i.e., $\mathcal {M}_{1}$ is true), then we have 2.66 times more evidence for the effect than we do for the null, but if we assume bias is extreme (i.e., $\mathcal {M}_{2}$ is true), then we have 1.92 times more evidence for the null than we do for the effect. Right panel: Prior and posterior distributions over the true value of the effect size Hedges’ g. Both distributions have point masses at g = 0 (i.e., a probability that the effect size is exactly zero owing to the inclusion of the four no-effect models), which are displayed as bars. The posterior distribution at 0 is lower than the prior, indicating that the data support the effect slightly more than the null. Aggregated over all models, there is 1.59 times more evidence for the effect than there is for the null $(1.59 = \frac {1}{0.63})$

The posterior distribution (black bars) quantifies what we know intuitively: a significant t value results either from a true effect reported in an unbiased world, or no true effect and an active biasing process. From the posterior distribution, we also learn that if we assume there is no publication bias, then there is about 2.66 times as much evidence for the alternative hypothesis as there is for the null (by comparing the two leftmost black bars). If we assume there is extreme bias, there is about 1.92 times as much evidence for the null as there is for the alternative (by comparing the next two black bars).

The right panel of Fig. 4 shows the prior and posterior distributions of the effect size parameter. Since half of the models under consideration predict an effect size of exactly zero, the prior and posterior probabilities of this null hypothesis are shown as bars in the figure. The panel shows that the data reported by Balcetis and Dunning (2010) do not deliver convincing evidence regarding the effect. The probability that g = 0 is slightly lower after observing the data than it was before (the Bayes factor $\mathcal {B}$ in favor of the null hypothesis is 0.63).

In order to evaluate the sensitivity of our method to the prior assumptions, we repeated the analysis under three scenarios that differ in the prior. In alternative scenario 1, we give prior weight only to $\mathcal {M}_{1}$. This is equivalent to a default Bayesian t test using a unit-information Bayes factor (as in Rouder, Speckman, Sun, Morey, & Iverson, 2009), and yields a Bayes factor $\mathcal {B} = 2.81$ against the null. In alternative scenario 2, we distribute prior weight over $\mathcal {M}_{1}$ and $\mathcal {M}_{2}$. This leads to a very similar inference but with a spike-and-slab prior on the effect size that has a spike at g = 0. Now $\mathcal {B} = 1.34$ against the null. In scenario 3, we consider only the models that allow for an effect size ($\mathcal {M}_{1+}$, $\mathcal {M}_{2+}$, $\mathcal {M}_{3+}$, and $\mathcal {M}_{4+}$). Including the possibility of bias turns the balance of evidence: $\mathcal {B} = 0.96$.

Our primary analysis described above allows for both true null effects and publication bias, and there the evidence for the null was even stronger. It is clear from this example that the outcome of revisiting a single empirical result depends to some extent on whether we are willing to consider that the effect may be truly zero, and whether we are willing to consider the possibility of a biased publication process. However, the analysis as presented here (in Fig. 4) allows for nuanced conclusions to accommodate different prior assumptions.

Meta-analysis: depression

Using the statistical mitigation approach, we can also mitigate the effects of publication bias in meta-analyses. In this section, we consider Bolier et al.’s 2013 meta-analysis of the effectiveness of positive psychology interventions. Bolier et al.focused on the effects of positive psychology interventions on subjective well-being, psychological well-being, and depressive symptoms. We will focus on the effects on depressive symptoms. The authors included a total of 14 studies that looked at positive psychology interventions on depression. We extracted the focal statistics (z-values) directly from Fig. 4 in the original article, and used those z values for our mitigation analysis.

The results are depicted in Fig. 5. The left panel shows the prior and posterior probabilities over models. We observe large increases in probability from prior to posterior in both models $\mathcal {M}_{3-}$ and $\mathcal {M}_{4-}$, the two more complex biasing models under the assumption that the null hypothesis is true. In addition, model $\mathcal {M}_{1-}$ with no bias under the assumption that the null is true also receives considerable weight: 8.48 times more than the no-bias model with an effect ($\mathcal {M}_{1+}$). Results show next to no evidence in support of any model that assumes the null hypothesis is false. The right panel shows the prior and posterior probability distributions of the effect size parameter z. The large weight of the various null-effect models is seen here in the increased posterior density at z = 0. The Bayes factor in favor of the null hypothesis is 27.81, making the posterior probability of the null approximately 96.5 %.

Fig. 5

Results for the depression meta-analysis. Left panel: Prior and posterior probabilities over models. The most weight (and largest shift) is seen in the models that suppose constant or exponential bias, with true effect size zero. The extreme-bias model ($\mathcal {M}_{2}$) is falsified by the presence of non-significant results. Within each biasing model, the posterior probability of the null model is much higher than that of the effect model. Right panel: Prior and posterior distributions over the true value of the test statistic z. The point mass at z = 0 is approximately 62.2 % higher under the posterior than under the prior. Given that the prior point mass on z = 0 was 50 % and the maximum shift is therefore by a factor of 2, this indicates a sizeable shift in the weight of evidence towards the null value

Meta-analysis: sleep quality

In this section, we consider another meta-analysis. Casement and Swanson (2012) conducted a meta-analysis of imagery rehearsal therapy for post-trauma nightmares; aggregating results from nine papers. The original analysis evaluated the effect of imagery rehearsal on three measures: nightmare frequency, sleep quality, and posttraumatic stress. We will revisit the effect on sleep quality (as measured by the Pittsburgh Sleep Quality Index or PSQI). We obtained the focal statistics from each of the nine individual studies listed in Table 2 (p. 571) of Casement and Swanson (2012).⁴

The Bayesian mitigation results of this meta-analysis are summarized in Fig. 6. From the left panel, it is clear that the most posterior weight is given to $\mathcal {M}_{1+}$, the model under which there is no bias and the null hypothesis is false (i.e., there is an effect of imagery rehearsal on sleep quality). The rest of the models receive negligible weight. In the right panel, we show the prior and posterior distributions of the effect parameter measured in terms of z values. It is evident here that the meta-analysis data from Casement and Swanson (2012) indeed changes the information about the effect. The posterior mean z is approximately 0.614, and the probability density at z = 0 is essentially zero—it is trillions of times lower after observing the data than before (Bayes factor against the null: 7 × 10¹⁵). Overall, our results show that after taking into account the possibility of various forms of publication bias, this meta-analysis indicates that imagery rehearsal is indeed effective in improving sleep quality.

Fig. 6

Results for the sleep quality meta-analysis. Left panel: Prior and posterior probabilities over models. The exact posterior probabilities are printed. Right panel: Prior and posterior distributions over the true value of z. The point mass at z = 0 is negligible under the posterior, indicating a strong shift in the weight of evidence towards the hypothesis that there is a non-zero effect

Discussion

We have outlined a novel method for inference regarding published effects. Our method is based on the assumption that there may be processes biasing the visibility of empirical studies, and relies on probability calculus to perform inference conditional on this possibility. The method has many desirable qualities that resonate well with intuitions researchers have about science and statistics. All that is required to apply the method is the published effect sizes. Sets of studies that consist exclusively of just-significant findings—which indicates that bias is likely, and non-significant findings are disproportionally hidden from the literature—are rendered inconclusive or indicative of only very small effects, while sets that contain effects of various sizes (including non-significant ones) provide more evidence for relatively larger effects. Unlike classical null hypothesis significance testing, our Bayesian method allows for the affirmation of the null hypothesis as well as its falsification, in addition to allowing for the inclusion of prior information.

Throughout, we focus on the empirical literature on a topic as the population of interest: For the purposes of effect size estimation across papers, all included studies should report on the same effect so that our mitigated effect size has a clear interpretation. However, we do not see the model probabilities as parameters to be estimated for any population. Instead, we think of the entire biasing process as an inhomogeneous mixture of various censoring mechanisms. Any given paper, under a given set of fleeting circumstances, may fit the assumptions of any model or some combination of them.

There are some potential caveats with the approach we present here. First, there is the issue that assuming the possibility of publication bias makes the analysis overly conservative in the case where publication bias does not occur. However, we believe that in most common-use cases, this is not a concern as we know publication bias to be a widespread issue. More generally, our method requires the explicit inclusion of domain knowledge in the formulation of the biasing processes, their relative probabilities, and the prior distribution of the effect sizes. We believe the assumptions we have chosen are (a) both sensible and in line with what is known of the field and (b) superior to the assumption of no publication bias that is implicit in all classical analyses.

Second, the censoring processes that we propose all assume that significant results are always published. Clearly this is not the case—papers submitted for publication are often rejected even bearing statistically significant results. However, we do not believe that there exists any systematic suppression of results because they were statistically significant to such an extent that it is skewing the literature at a scale comparable to the bias against the null. Furthermore, it is reasonable to assume that those papers with significant results that are not published often have issues unrelated to the outcome, for example with the experimental design (which would preclude use in meta-analysis in its own right). Finally, if indeed a nonignorable fraction of significant results goes unpublished, randomly, even though the applied methods are sound, then a valid interpretation of our censoring functions is simply that they describe the probability of publication of a nonsignificant result relative to the probability of publication of a significant result, with as only restriction that the former is no greater than the latter, which we consider a very weak assumption.

Third, there may be other biasing mechanisms in addition to the ones we propose here. However, we believe that the set of processes we consider spans a reasonably large range of possible mechanisms—that is, we struggle to think of biasing mechanisms that will yield fundamentally different censoring functions. One possible exception is a practice known as “hypothesizing after the results are known” (HARKing), which may in fact cause an overrepresentation of results that are clearly nonsignificant (e.g., p > .50), because these results are declared non-pivotal after they are known, and are then reported parenthetically in a paper with a different focal test. We decided not to include a HARKing model here because such a model would apply to a different set of observations (such as “non-pivotal statistics,” which are published statistics that are not used to support inference regarding a new finding or that are otherwise irrelevant for the main narrative of a paper; e.g., manipulation checks and failed secondary manipulations). A possible HARKing model is formally very similar to $\mathcal {M}_{4}$, but predicts that the probability of publishing nonsignificant findings increases as e ^−γ(1−p). Another biasing mechanism for which we do not currently account for is academic fraud.

Fourth, our meta-analyses as we have implemented them here make the assumption of independence between studies. In practice, this assumption may be wrong and biases may tend to be correlated (positively in the case of labs repeatedly publishing on the same topic, but negatively in the case of adversarial replication attempts).⁵ Our Bayesian model averaging framework allows us to account for correlated bias in the same way we deal with other unknowns: marginalization over the unknown quantity. We provide the equations for such an exercise in Appendix B, but leave the implementation of this analysis aside until a computationally efficient treatment for this case is developed.

Finally, we wish to emphasize again the subjectivity of some of the assumptions we have made, and the fact that reasonable people can reasonably disagree in the case of differing prior assumptions. The method that we have outlined allows for the inclusion of a wide variety of prior assumptions, and it may be improved by further psychological research in the behavioral processes of publication bias.

Appendices

Appendix A: Behavioral models of publication bias

Here we detail the behavioral models of publication bias that we employ to mitigate the effects of bias on reported effect sizes, and we describe the details of the Bayesian inference methods that we apply to these models. For convenience of exposition, we will focus on unpaired t tests, but the method extends to other parametric tests based on p values.

In the description of the models that follows, p(⋅) will indicate a likelihood function, t(⋅|ν) will indicate the probability density function of a central t distribution with ν degrees of freedom and t’(⋅|x,ν) of the noncentral t distribution with noncentrality parameter x. T(⋅|ν) and T’(⋅|x,ν) indicate their respective cumulative distribution functions. n ₁ and n ₂ will be the sample sizes in two groups. δ ^obs will indicate a test statistic (TS) obtained from the sample. A ‘true’ effect size (ES) will be indicated η ^true. The mitigated TS δ ^mit is our estimate of the true TS.

Throughout, it is important to note that, given a sample size and a design, any TS uniquely maps to an ES. For example, for the unpaired t test, η ^true=φ δ ^true with $\varphi = \sqrt {\frac {n_{1}+n_{2}}{n_{1}n_{2}}}$. Transformations for other inferential tests are well known (e.g., Ellis, 2010; or succinctly in Footnote 4 of Verhagen & Wagenmakers, 2014). To define a prior for the TS, we propose a unit information prior on the ES η ^true: η ^true∼N(0,1). We can readily transform this prior to the scale of the TS: $\left (\delta ^{true}\left |\mathcal {M}_{+}\right .\right ) \sim \mathrm {N}\left ({0},{\varphi ^{2}}\right )$, where $\mathcal {M}{+}$ indicates any model under which the null hypothesis η ^true = 0 is false. The prior might also be generalized to $\left (\delta ^{true}\left |\mathcal {M}_{+}\right .\right ) \sim \mathrm {N}\left ({\varphi \mu },{\varphi ^{2}\sigma ^{2}}\right )$, to either reduce the slightly assumptive nature of the unit information prior or to incorporate genuine prior knowledge.

The available data are n ₁ and n ₂ and the observed TS δ ^obs of at least one experiment. Associated with δ ^obs is an observed p value p ^obs=2×T(−|δ ^obs||ν). Below, we give the likelihood functions associated with each of the four behavioral models of publication bias, under each of the two states of nature (H ₀ false or true).

$\mathcal {M}_{1}$: a no-bias model

Suppose $\mathcal {M}_{1}$::

There is no publication bias. The probability of publishing, P _{p u b} , is 1.

Case $\mathcal {M}_{1+}$::

H ₀ false $p\left (\delta ^{obs}\left |\mathcal {M}_{1+},\eta ^{true}\right .\right ) = t\text {'}\left (\delta ^{obs}\left |\right .\right .$ η ^true,ν), with true ES η ^true. Case $\mathcal {M}_{1-}$: H ₀ true $p\left (\delta ^{obs}\left |\mathcal {M}_{1-},\eta ^{true}\right . \right ) = t\left (\delta ^{obs}\left |\right .\right .$ ν), with ν degrees of freedom.

$\mathcal {M}_{2}$: an extreme-bias model

Suppose $\mathcal {M}_{2}$: Publication bias is extreme—publication only happens if significance is found. The probability of publishing, P _{p u b} , is a step function of p ^obs:

$$P_{pub}\left( p^{obs}\right) = \left\{ \begin{array}{l l} 0 & \text{if}~p^{obs} \geq \alpha\\ 1 & \text{otherwise} \end{array} \right. . $$

where p ^obs is a function of the observed TS δ ^obs, as above, and α is conventionally set to .05. Associated with α is the critical TS δ ^crit, which is the smallest TS (in absolute value) to be considered significant at level α (i.e., any TS under −δ ^crit or above δ ^crit would be considered statistically significant).

Case $\mathcal {M}_{2+}$::

H ₀ false

$$p\!\left( \delta^{obs}\!\left|\mathcal{M}_{2+},\eta^{true}\right.\right)\! =\! \left\{\!\begin{array}{l l} 0 & \text{if} p^{obs} \geq \alpha\\ \frac{1}{B_{2}} t\text{'} \left( \delta^{obs}\left|\eta^{true},\nu\right. \right) &\text{otherwise} \end{array} \right. , $$

or the t’ distribution truncated to the significance region. Note that the denominator B ₂ can be computed without the need for expensive numerical methods, using the direct calculation of the cumulative noncentral t distribution T’:

$$\begin{array}{@{}rcl@{}} B_{2}\! &=&\! {\int}^{-\delta^{crit}}_{-\infty}t\text{'}\left( x\left|\eta^{true},\nu\right.\right)dx + {\int}^{+\infty}_{\delta^{crit}}t\text{'}\left( x\left|\eta^{true},\nu\right.\right)dx\\ &=& T\text{'}\left( -\delta^{crit}\left|\eta^{true},\nu\right.\right) + 1 - T\text{'}\left( \delta^{crit}\left|\eta^{true},\nu\right.\right). \end{array} $$

Case $\mathcal {M}_{2-}$::

H ₀ true

$$\begin{array}{@{}rcl@{}} &&p\left( \delta^{obs}\left|\mathcal{M}_{2-}\right.\right)\\ &&= \left\{ \begin{array}{l l} 0 & \text{if} p^{obs} \geq \alpha\\ \frac{t\left( \delta^{obs}\left|\nu\right.\right)}{{\int}_{-\infty}^{-\delta^{crit}}t\left( x\left|\nu\right.\right)dx + {\int}^{+\infty}_{\delta^{crit}}t\left( x\left|\nu\right.\right)dx} = \frac{1}{\alpha}t\left( \delta^{obs}\left|\nu\right.\right) &\text{otherwise} \end{array} \right. , \end{array} $$

that is, the t distribution truncated to the region that yields statistical significance.

$\mathcal {M}_{3}$: a constant-bias model inspired by Greenwald

Greenwald (1975) proposed a model of the research-publication process in which a number of parameters characterize the various steps of publishing in psychology, such as the investigators’ probability of reporting research and the editors’ probability of publishing manuscripts reporting significant or nonsignificant results. We simplify this model by summarizing the probabilities in each step into one single constant probability of publishing nonsignificant results.

Suppose $\mathcal {M}_{3}$: Publication occurs with probability 1 if a significant effect is found, but also with some constant probability π if no significant effect is found. The probability of publishing, P _{p u b} , is

$$P_{pub}\left( p^{obs}, \pi\right) = \left\{ \begin{array}{l l} \pi & \text{if} p^{obs} \geq \alpha\\ 1 & \text{otherwise} \end{array} \right. . $$

Case $\mathcal {M}_{3+}$::

H ₀ false

$$p\left( \delta^{obs}\left|\mathcal{M}_{3+},\eta^{true},\pi\right.\right) = \left\{ \begin{array}{l l} \pi \frac{1}{B_{3}} t\text{'}\left( \delta^{obs}\left|\eta^{true},\nu\right.\right) & \text{if}~p^{obs} \geq \alpha\\ \frac{1}{B_{3}} t\text{'}\left( \delta^{obs}\left|\eta^{true},\nu\right.\right) & \text{otherwise} \end{array} \right. , $$

where 0 ≤ π ≤ 1 with prior π∼U(0,1), and

$$\begin{array}{@{}rcl@{}} B_{3}\! &=&\! \pi{\int}^{\delta^{crit}}_{-\delta^{crit}}t\text{'}\left( x\left|\eta^{true},\nu\right.\right)dx\! +\! {\int}^{+\infty}_{\delta^{crit}}t\text{'}\left( x\left|\eta^{true},\nu\right.\right)dx\\ &&+ {\int}^{-\delta^{crit}}_{-\infty}t\text{'}\left( x\left|\eta^{true},\nu\right.\right)dx \\ &=& 1 - \left( 1-\pi\right) \left[ T\text{'}\left( \delta^{crit}\left|\eta^{true},\nu\right.\right)\right.\\ &&\qquad\qquad\quad{\kern3pt}\left. - T\text{'}\left( -\delta^{crit}\left|\eta^{true},\nu\right.\right)\right]. \end{array} $$

Case $\mathcal {M}_{3-}$::

H ₀ true

$$p\left( \delta^{obs}\left|\mathcal{M}_{3-},\pi\right.\right) = \left\{\begin{array}{l l} \pi\frac{1}{A_{3}} t\left( \delta^{obs}\left|\nu\right.\right) & \text{if} p^{obs} \geq \alpha\\ \frac{1}{A_{3}} t\left( \delta^{obs}\left|\nu\right.\right) & \text{otherwise} \end{array} \right. , $$

where $A_{3} = \pi {\int }^{\delta ^{crit}}_{-\delta ^{crit}}t\left (x\left |\nu \right .\right )dx + 2{\int }^{+\infty }_{\delta ^{crit}}t\left (x\left |\nu \right .\right )dx = \pi \left (1-\alpha \right ) + \alpha$.

$\mathcal {M}_{4}$: an exponential-bias model inspired by Givens

In Givens et al. (1997), another approach is introduced to estimate and adjust for publication bias, by partitioning the unit interval into segments so that a p value from any given study falls into one of these regions. Each interval region is assigned a corresponding probability of publication, with probabilities decreasing as the region departs from significance. In $\mathcal {M}_{4}$, we capture this same concept with a probability of publishing that decreases exponentially as a function of the difference between the observed p value p ^obs and α. The rate of exponential decay as p ^obs departs from α is determined by a strictly positive rate parameter λ. A priori, we suppose λ∼Exp(5).

Suppose $\mathcal {M}_{4}$: Publication occurs with certainty if a significant effect is found, but also with some nonzero probability if no significant effect is found.

$$P_{pub}\left( p^{obs},\lambda\right) = \left\{ \begin{array}{l r} e^{-\lambda \left( p^{obs}-\alpha\right)} & \text{if} p^{obs} \geq \alpha\\ 1 & \text{otherwise} \end{array} \right. . $$

Case $\mathcal {M}_{4+}$::

H ₀ false

$$p\!\left( \!\delta^{obs}\!\left|\mathcal{M}_{4+},\!\eta^{true},\!\lambda\!\right.\right) \! =\! \left\{\! \begin{array}{l r} e^{-\lambda \left( p^{obs}-\alpha\right)} \frac{1}{B_{4}} t\text{'}\left( \delta^{obs}\left|\eta^{true},\nu\right.\right) \text{if}~p^{obs} \geq \alpha\\ \frac{1}{B_{4}} t\text{'}\left( \delta^{obs}\left|\eta^{true},\nu\right.\right) \qquad\qquad\quad\text{otherwise} \end{array} \right.\! , $$

where

$$\begin{array}{@{}rcl@{}} B_{4}\! &=&\! {\int}^{\delta^{crit}}_{-\delta^{crit}} e^{-\lambda \left( p\left( x, \nu\right)-\alpha\right)}t\text{'}\left( x\left|\eta^{true},\nu\right.\right)dx\\ &&+ {\int}^{+\infty}_{\delta^{crit}}t\text{'}\left( x\left|\eta^{true},\nu\right.\right)dx + {\int}^{-\delta^{crit}}_{-\infty}t\text{'}\!\left( x\left|\eta^{true},\nu\right.\right)dx\\ &=&\! {\int}^{\delta^{crit}}_{-\delta^{crit}} e^{-\lambda \left( p\left( x, \nu\right)-\alpha\right)}t\text{'}\left( x\left|\eta^{true},\nu\right.\right)dx\\ &&+ \left[1 - T\text{'}\left( \delta^{crit}\left|\eta^{true},\nu\right.\right)\right] + T\text{'}\left( -\delta^{crit}\left|\eta^{true},\nu\right.\right)dx. \end{array} $$

with p(x, ν) = 2 × T(−|x||ν), the p value associated with a particular observation given ν degrees of freedom.

Case $\mathcal {M}_{4-}$::

H ₀ true

$$p\left( \delta^{obs}\left|\mathcal{M}_{4-},\lambda\right.\right) = \left\{ \begin{array}{l r} e^{-\lambda \left( p^{obs}-\alpha\right)} \frac{1}{A_{4}} t\left( \delta^{obs}\left|\nu\right.\right) & \text{if} p^{obs} \geq \alpha\\ \frac{1}{A_{4}} t\left( \delta^{obs}\left|\nu\right.\right) &\text{otherwise} \end{array} \right. , $$

where

$$\begin{array}{@{}rcl@{}} A_{4} &=& {\int}^{\delta^{crit}}_{-\delta^{crit}} e^{-\lambda \left( p\left( x, \nu\right)-\alpha\right)}t\left( x\left|\nu\right.\right)dx +2 {\int}^{+\infty}_{\delta^{crit}}t\left( x\left|\nu\right.\right)dx \\ &=& {\int}^{\delta^{crit}}_{-\delta^{crit}} e^{-\lambda \left( p\left( x, \nu\right)-\alpha\right)}t\left( x\left|\nu\right.\right)dx + \alpha. \end{array} $$

Appendix B: Bayesian inference details

Computation of Jeffreys weights

A standard Bayesian approach to model comparison is the Bayes factor (Jeffreys, 1961; Kass and Raftery, 1995). Bayes factors summarize the evidence provided by the observed data in favor of one model over another, and implicitly control for goodness-of-fit as well as model complexity. The Bayes factor $\mathcal {B}$ between two models is simply the ratio of Bayesian evidence, also known as the marginal likelihood, for each model. The Bayesian evidence $\mathcal {E}$ is computed by integrating the likelihood over the prior parameter space, so that the Bayes factor between two models, $\mathcal {M}_{1+}$ and $\mathcal {M}_{2-}$, denoted $\mathcal {B}\left ({\mathcal {M}_{1+}}:{\mathcal {M}_{2-}}\right )$ is:

$$\begin{array}{@{}rcl@{}} \mathcal{B}\left( {\mathcal{M}_{1+}}:{\mathcal{M}_{2-}}\right) &=& \frac{\mathcal{E}_{1+}}{\mathcal{E}_{2-}}\\ &=& \frac{\int{p\left( x\left|\theta_{1},\mathcal{M}_{1+}\right.\right)p\left( \theta_{1}\left|\mathcal{M}_{1+}\right.\right)d\theta_{1}}} {\int{p\left( x\left|\theta_{2},\mathcal{M}_{2-}\right.\right)p\left( \theta_{2}\left|\mathcal{M}_{2-}\right.\right)d\theta_{2}}} \end{array} $$

where $p\left (x\left |\theta _{2},\mathcal {M}_{2-}\right .\right )$ is the data-dependent likelihood for $\mathcal {M}_{2-}$, $p\left (\theta _{1}\left |\mathcal {M}_{1+}\right .\right )$ is the prior distribution over the parameters of $\mathcal {M}_{1+}$, and the conditioning of the evidences and Bayes factor on the data x is implicit. In our case, the computation of the Bayes factors between these two models is nontrivial but not prohibitive. If |δ ^obs|<|δ ^crit|, $\mathcal {B}\left ({\mathcal {M}_{1+}}:{\mathcal {M}_{2-}}\right ) = +\infty$, because this is an impossible occurrence under $\mathcal {M}_{2-}$. Otherwise,

$$\mathcal{B}\left( {\mathcal{M}_{1+}}:{\mathcal{M}_{2-}}\right) = \alpha \frac{\int t\text{'}\left( \delta^{obs}\left|\eta^{true},\nu\right.\right)\mathrm{N}\left( {\eta^{true}\left|0\right.}{\sqrt{n}}\right)d\eta^{true}}{t\left( \delta^{obs}\left|\nu\right.\right)}. $$

Note that the integral in the denominator disappears because model $\mathcal {M}_{2-}$ has no random parameters. The integral in the numerator can be efficiently approximated with numerical methods such as Gaussian quadrature (Abramowitz et al. 1972).

The Bayes factor is the ratio of the posterior odds of one model to its prior odds, regardless of the actual value of the prior odds. Because it is an odds ratio, it has a convenient and intuitive interpretation. If $\mathcal {B}\left ({\mathcal {M}_{1+}}:{\mathcal {M}_{2-}}\right )$ is greater than 1, then $\mathcal {M}_{1+}$ is more strongly supported by the observed data than $\mathcal {M}_{2-}$. Similarly, if $\mathcal {B}\left ({\mathcal {M}_{1+}}:{\mathcal {M}_{2-}}\right )$ is less than 1, then $\mathcal {M}_{2-}$ is more strongly supported by the observed data than $\mathcal {M}_{1+}$. Intuitively, it quantifies how much one should update one’s prior beliefs about the models under consideration, given evidence from the observed data. The Bayes factor also operates nicely on a continuum, as opposed to classical NHST in which a p value is judged against a single arbitrary cut-off criterion α. Jeffreys (1961) suggests some interpretative boundaries, with values of 3, 10, and 30 corresponding to strengths of evidence that are “barely worth a mention,” “substantial,” and “strong,” respectively.

Jeffreys weights are a multi-alternative extension of Bayes factors, taking the Bayesian evidence for each model and normalizing by the sum of evidences over all models under consideration (Vandekerckhove, Matzke, & Wagenmakers, 2015). For our eight models, if the evidence for $\mathcal {M}_{k}$ is denoted $\mathcal {E}_{k}$, then the corresponding Jeffreys weight $\mathcal {J}_{k}$ is:

$$\mathcal{J}_{k} = \frac{\mathcal{E}_{k}}{{\sum}_{j=1}^{8} \mathcal{E}_{j}}.$$

Jeffreys weights can be multiplied with model priors to arrive at model posterior probabilities:

$$P\left( \mathcal{M}_{k}\left| x\right.\right) = \frac{\mathcal{J}_{k}P\left( \mathcal{M}_{k}\right)}{{\sum}_{j=1}^{8} \mathcal{J}_{j}P\left( \mathcal{M}_{j}\right)}.$$

Model priors

We need to define a prior distribution over the eight possible models $\mathcal {M}_{1+}, \ldots , \mathcal {M}_{4-}$. In selecting our prior over models, we followed three main desiderata. First, we hold that observing a single significant TS should not allow us to differentiate between a no-bias model and an extreme-bias model with the same true effect size. Given that $\mathcal {B}\left ({\mathcal {M}_{1-}}:{\mathcal {M}_{2-}}\right ) = \alpha$, we decide that the prior for these models must reflect that ratio, so that $P\left (\mathcal {M}_{1-}\right ) = P\left (\mathcal {M}_{2-}\right ) / \alpha$. Not scaling $P\left (\mathcal {M}_{2-}\right )$ by at least 1/α would cause a single significant observation to lead us to conclude that publication bias occurred.⁶ Additionally, we do not want the prior to prefer either of the two states of nature: $\forall i: p\left (\mathcal {M}_{i-}\right ) = p\left (\mathcal {M}_{i+}\right )$. Finally, we want the prior to express prior equiprobability among all the biasing mechanisms (not including the no-bias mechanism). Taking all these desiderata together, the prior over models is defined as (20,20,1,1,1,1,1,1)/46, and this is the prior pictured in Figs. 4, 5, and 6.

Aggregation of information across studies

Given multiple independent studies s, each with a unique observed TS $\delta ^{obs}_{s}$, the aggregated posterior distribution of δ ^mit is obtained by first applying Bayes’ theorem, then implementing the independence assumption, and then marginalizing over models:

$$\begin{array}{@{}rcl@{}} p\left( \delta^{mit}\left|\left\{\delta^{obs}_{s}\right\}_{1}^{S}\right.\right) &\propto& p\left( \delta^{mit}\right)p\left( \left\{\delta^{obs}_{s}\right\}_{1}^{S}\left|\delta^{mit}\right.\right) \\ &\propto& p\left( \delta^{mit}\right)\prod\nolimits_{s=1}^{S} p\left( \delta^{obs}_{s}\left|\delta^{mit}\right.\right) \\ &\propto& p\left( \delta^{mit}\right)\prod\nolimits_{s=1}^{S} \sum\limits_{\mathcal{M}} p\left( \delta^{obs}_{s}\left|\delta^{mit},\mathcal{M}\right.\right)\\ &&\times P\left( \mathcal{M}\left|\left\{\delta^{obs}_{s}\right.\right\}_{1}^{S}\right), \end{array} $$

and finally, computing the normalizing constant, so that

$$\begin{array}{@{}rcl@{}} &&p\left( \delta^{mit}\left|\left\{\delta^{obs}_{s}\right\}_{1}^{S}\right.\right)\\ &&= \displaystyle \frac{p\left( \delta^{mit}\right){\prod}_{s=1}^{S} {\sum}_{\mathcal{M}} p\left( \delta^{obs}_{s}\left|\delta^{mit},\mathcal{M}\right.\right)P\left( \mathcal{M}\left|\left\{\delta^{obs}_{s}\right\}_{1}^{S}\right.\right)}{{\int}_{-\infty}^{\infty} p\left( x\right){\prod}_{s=1}^{S} {\sum}_{\mathcal{M}} p\left( \delta^{obs}_{s}\left|x,\mathcal{M}\right.\right)P\left( \mathcal{M}\left|\left\{\delta^{obs}_{s}\right\}_{1}^{S}\right.\right)dx}. \end{array} $$

(1)

In cases where the independence assumption is violated or not desired, a correlated error structure can instead be explicitly modeled, so that the effect size factor in the likelihood function becomes $\mathrm {N}({\left \{\varphi _{s}\delta ^{obs}_{s}\right \}_{1}^{S}}|{\left \{\varphi _{s}\delta ^{mit}\right \}_{1}^{S}},{\Sigma }),$ with Σ ∈ R _{S × S} . Unfortunately, the evaluation of the associated posterior distribution would require the repeated computation of an integral over the space of all covariance matrices, which is currently prohibitively expensive.