Introduction

Arabic and verbal numbers are the most widely used symbols for encoding magnitude (e.g., Shepard, Kilpatric, & Cunningham, 1975). However, not only numbers encode magnitude, but also quantifiers (e.g., “a few”, “many”, “at least”) and units of measurement (e.g., kilometers, seconds, or milligrams) convey magnitude information. Recently, research in processing of magnitude encoded by quantifiers has received increasing interest (e.g., Wei, Chen, Yang, Zhang, & Zhou, 2014). However, magnitude processing involving units of measurement is still a neglected topic in numerical cognition research. Hence, in the present study, we examined magnitude processing of measurement units and their relation to previous findings on multi-digit number processing using a magnitude comparison task.

The magnitude of a physical quantity (e.g., 6 cm, 30 s, or 73 kg) is indicated by a quantifying number and a measurement unit (e.g., cm, s, or kg). For most metric measures, such as meter and gram, indicating length and weight, respectively, metric prefixes (e.g., ‘k’ = kilo) of base units are used to specify larger or smaller instances (e.g., 8 cm reflects 8 × 10-2 m but 8 km reflects 8 × 103 m). When comparing two physical quantities, either the quantifying number or the measurement unit is decisive: when two physical quantities have the same measurement unit, for instance, 6 cm versus 8 cm, the larger of the physical quantities can be identified by evaluating the larger number. However, when two physical quantities have different measurement units but numbers within a similar range (e.g., 0–9), the larger of them can be singled out based on the measurement unit. For instance, 8 cm is larger than 6 mm, since centimeters are ten times larger than millimeters. However, in this compatible example, the comparison of numbers also leads to the correct solution of 8 cm being larger than 6 mm. Nevertheless, the comparison of numbers can also be incompatible with the comparison of measurement units. For instance, when given 6 cm versus 8 mm, comparing the numbers would result in a wrong answer.

Quite similar to recent observations for two-digit numbers, these properties of measurement units can lead to decision biases either compatible or incompatible with the overall decision. For between-decade number pairs (e.g., 42_57), the larger of two numbers can be inferred from comparing the tens only. However, even when the unit digit is not decision relevant, the units still influence the comparison process: when the comparison of units is compatible with the comparison of tens (e.g., 42_57, with 4 < 5 and 2 < 7), reaction times (RT) are faster and error rates lower than when separate comparisons of tens and units are incompatible (e.g. 37 vs 52, with 3 < 5 but 7 > 2; termed the unit-decade compatibility effect; Nuerk, Weger, and Willmes (2001). This unit-decade-compatibility effect indicates that tens and units are processed separately. Thereby, automatic processing of the units interferes with processing of the tens. Huber, Cornelesen, Moeller, and Nuerk (2014a) showed that a conceptually identical compatibility effect can also be found when comparing symbols and numbers. More specifically, Huber et al. (2014a) observed a compatibility effect for the polarity sign and the digit next to the polarity sign (e.g., the decade digit in the case of two-digit numbers). Separate comparison of polarity signs and digits can analogously be described as either compatible (e.g., –2_+7, – < + and 2 < 7) or incompatible (e.g., –7_+2, – < + but 7 > 2) with the overall decision. Thus, a sign-digit compatibility effect is observed whenever participants process polarity signs and digits in a componential manner. In line with this, Huber et al. (2014a) found that participants’ response times were slower when comparing sign-decade incompatible as compared to compatible two-digit number pairs.

Based on these results, Huber et al. (2014a) proposed a general model framework for multi-symbol number processing suggesting that multi-symbol number strings that consist of both digits and characters have common processing characteristics. Thus, irrespective of whether a multi-symbol number consists of digits only (e.g., 28) or of digits and other characters (e.g., –28), the constituents of the respective multi-symbol number should be processed and compared to each other separately in a componential manner.

Importantly, following this generalized model framework account, physical quantities (e.g., 3 m) should also be understood as multi-symbol numbers. Accordingly, this hypothesis suggests that the constituents of physical quantities (i.e., numbers and measurement units) should be processed separately in a componential manner. Therefore, a compatibility effect as previously demonstrated for polarity signs and digits should be observed when comparing physical quantities as well. In this vein, comparing incompatible pairs of physical quantities/lengths (e.g., 1 cm vs 4 mm, with 1 < 4, but cm > mm) should result in slower RT and higher error rates than compatible pairs of physical quantities/lengths (e.g., 1 mm vs 4 cm, with 1 < 4 and mm < cm).

Additionally, magnitude information is conveyed not only by numbers and measurement units, but also by the number of characters in a number string. Recently, Huber, Klein, Willmes, Nuerk, and Moeller (2014b) observed a string length congruity effect when comparing two decimal fractions differing in their number of digits (see also Kallai & Tzelgov, 2014). For string length incongruent trials for which the numerically larger decimal fraction consisted of fewer digits than the numerically smaller decimal fraction (e.g., 7.14_7.6 with 1 < 6, but 3 > 2 digits), participants’ response times were longer and error rates higher. In contrast, participants’ responses were faster and less error-prone for string length congruent pairs in which the numerically larger decimal fraction consisted of more digits than the numerically smaller decimal fraction (e.g., 2.7_2.91 with 7 < 9 and 2 < 3 digits).

The string length congruity effect reveals that compatibility might not be the only quality influencing processing of physical quantities: if string length generally influences processing of numerical information, we should observe a congruity effect for physical quantities as well. For instance, the comparison of 6 m vs 4 mm is string length incongruent, because the larger physical quantity/length 6 m is composed of two characters (the number “6” and the measurement unit “m”), whereas the smaller physical quantity 4 mm consists of three characters (the number “4” and the measurement unit mm composed of two “m”). In contrast, the comparison of 6 km and 4 m is string length congruent with the larger physical quantity 6 km consisting of more characters than the smaller physical quantity 4 m. In line with the string length congruity effect for decimal fractions, response times should be slower and error rates higher when processing string length incongruent as compared to string length congruent physical quantities.

The present study

The aim of the present study was straightforward: we were interested in whether the general componential processing model for multi-symbol number processing as proposed by Huber et al. (2014b) accounts for the magnitude processing of physical quantity as well (e.g., 6 m, 2 cm). In three magnitude comparison experiments, participants had to single out the longer one of two lengths, each consisting of a number and a length unit (i.e., km, m, cm, mm). In the first experiment, we examined the presence of compatibility as well as congruity effects in two subtasks using the same digits for compatible/string length congruent as well as incompatible/string length incongruent trials. However, using such a stimulus set leads to smaller holistic distances for incompatible compared to compatible trials (e.g., compatible: 9 cm vs 2 mm = 88 mm; incompatible: 2 cm vs 9 mm = 11 mm). To control for this potential confounder, we conducted a second experiment with matched holistic distances between compatible and incompatible length pairs. Finally, in Experiment 3, we examined whether a distance effect for measurement units exists. Because experiments were very similar regarding stimuli, design, and procedure, methods and results will be reported jointly followed by a general discussion.

Methods

Participants

Experiment 1

Twenty-eight native German-speaking adults (21 female, 7 left-handed) participated in Experiment 1. Mean age was 23.96 years (SD 3.76; range: 19–35 years). Participants received 4€ in compensation.

Experiment 2

Twenty-three native German-speaking adults (17 female, all right-handed) participated in Experiment 2. Mean age was 22.52 years (SD 3.07; range: 18–30 years). Participants received a monetary compensation of 2€.

Experiment 3

Twenty-four native German-speaking adults (20 female, all right-handed) participated in Experiment 3. Mean age was 22.96 years (SD 2.85; range: 19–29 years). Participants received 2€ in compensation.

All experiments were approved by the local ethics committee of the Knowledge Media Research Center (KMRC), Tuebingen.

Stimuli and design

In Experiment 1, stimuli were presented in two sub-tasks. In sub-task 1, a total of 240 lengths were constructed using single-digit numbers between 1 and 9 and the scale units millimeter (mm), centimeter (cm) and decimeter (dm). Stimuli were manipulated according to compatibility (compatible vs incompatible). For the scale unit combinations mm_cm and cm_dm, 30 compatible length pairs were constructed each (e.g., 1 mm_5 cm: 1 < 5 and mm < cm; 4 dm vs 2 cm: 4 > 2 and dm > cm). The two numbers of a length pair always differed. To ensure that stimuli differed only in factor compatibility, 30 incompatible length pairs were incorporated for both scale unit combinations by simply swapping the scale units of the two numbers (e.g., 1 cm_5 mm: 1 < 5, but cm > mm; 4 cm_2 dm: 4 > 2, but cm < dm). To prevent participants from focusing on the decisive scale unit only, 120 filler pairs were added (40 per scale unit). Filler pairs consisted of different numbers but the same scale unit (e.g., 2 cm_5 cm). The same number pairs were used for each scale unit.

In sub-task 2, for both the 120 experimental stimuli and the 120 filler length pairs, the same numbers as in sub-task 1 were used. However, scale units were changed to millimeter (mm), meter (m), and kilometer (km). Thereby, it was possible to manipulate both the factors compatibility (compatible vs incompatible) and string length congruity (congruent vs incongruent) orthogonally [compatible and length congruent (e.g., 1 m_2 km: 1 < 2 and m < km, length: 2 < 3 characters), compatible but length incongruent (e.g., 2 m_1 mm: 2 > 1 and m > mm, length: 2 < 3 characters), incompatible but length congruent (e.g., 1 km_2 m: 1 < 2 and km > m, length: 3 > 2 characters), and incompatible and length incongruent (e.g., 2 mm_1 m: 2 < 1 and mm < m, length: 3 > 2 characters)].

In Experiment 2, we used the same scale units as in sub-task 1 of Experiment 1 (i.e., mm, cm, and dm). However, in contrast to Experiment 1, we matched holistic distances linearly and logarithmically between compatible and incompatible items (mean linear distances for compatible: 25 cm vs incompatible: 25 cm; mean logarithmic distances for compatible: 7.20 cm vs incompatible: 7.18 cm). The stimulus set included 48 compatible and 48 incompatible numbers. Additionally, we added 96 filler items.

In Experiment 3, we varied the distances between scale units by including the following comparison pairs: mm_cm, mm_dm, mm_km, cm_dm, cm_km, and dm_km. Digits were the same as in Experiment 2. However, different to Experiment 2, we did not include filler items, as we were only interested whether a distance effect for measurement units exists. In sum, the stimulus set included 288 items (=48 × 6 items). Stimuli of all three experiments are given in the supplementary material.

Using a standard 19 inch (48 cm) screen, to-be-compared pairs were presented above each other in white against a black background (font: “Courier New”, font size: 60 pt, plain). Each number and its corresponding scale unit were separated by a blank space. Viewing distance was approximately 50 cm. The fixation point was positioned in the middle of the screen (512/384 pixels).

Task and procedure

Task and procedure were identical in all three experiments. Participants were instructed to indicate the longer of two simultaneously presented measurement units as fast and as accurately as possible. When the upper length was longer, participants had to press the ‘Z’ key of a standard QWERTZ keyboard with the right index finger. If the lower length was longer, the ‘B’ key had to be pressed with the left index finger. The first ten trials in each experiment were training trials chosen randomly from the experimental stimulus set. In all experiments, trials were presented in blocks of 80 trials with a short break between blocks. Items remained visible until a response key was pressed. During the inter-trial interval of 500 ms the fixation point for the next item was presented on the screen. Trial order was pseudo-randomized to prevent both pressing the same key and presenting items of the same category more than three times in a row. The position of the longer length was counterbalanced.

Analysis

In both Experiments 1 and 2, we excluded three participants from further data analysis due to high error rates around chance level in one of the conditions. Thus, in Experiment 1, analyses included 25 participants (19 female; 6 left-handed). Mean error rate was 5.7 % (SD = 3.1 %; range: 1.7–11.3 %). In Experiment 2, analyses included 20 participants (16 female). For this sample, mean error rate was 5.4 % (SD = 5.4 %; range: 0.0–24.0 %). In Experiment 3, all participants were included. Mean error rate was 3.6 % (SD = 4.4 %; range: 0.0–17.0 %).

Only correct trials were included in the RT analyses. Moreover, we excluded RTs outside the interval ± 3SD around the individual mean. In sum, we considered 92.7 % of all trials for RT analysis in Experiment 1, 93.2 % in Experiment 2, and 94.5 % in Experiment 3.

RT was analyzed using linear mixed models (LMM). Statistical analyses were run using R (R Development Core Team, 2014), and the R package lme4 for LMM analyses (Bates, Maechler, Bolker, & Walker, 2014). In line with the recommendation of Barr, Levy, Scheepers, and Tily (2013), we used the maximal random effects structure including random intercepts for participants and items as well as each fixed effect as random effect. However, in case LMMs did not converge, we removed random correlations. To obtain P-values, we used the Satterthwaite approximation for degrees of freedom available in the R package lmerTest (Kuznetsova, Brockhoff, & Christensen, 2014).

For sub-task 1 of Experiment 1, we considered compatibility of numbers and measurement unit (compatible vs incompatible) as a categorical and digit distance (ranging from 1 to 8) as a continuous predictor variable as well as their interaction. For sub-task 2, we included compatibility, string length congruity (congruent vs incongruent), and the interaction between compatibility and string length congruity as factors. In Experiment 2, the only factor considered was compatibility. In Experiment 3, we included distance between exponents of scale units (e.g., 1 mm = 10-3 m vs 1 cm = 10-2 m, and, thus, distance = |–3 –(–2)| = 1) as factor. Distance ranged from 1 to 6. Prior to data analysis, predictors were deviation coded (compatible = –0.5, incompatible = 0.5; congruent = –0.5, incongruent = 0.5) and continuous predictors were centered.

Results

A summary of statistical details for the analyses of RT data is given in Table 1. For additional analyses including analyses of error rate (ER) data see the supplementary material.

Table 1 Statistics of effects tested in Experiments 1, 2 and 3. Effects and confidence intervals (CI) are given in ms. Comp Compatibility of numbers and measurement units, Cong String length congruity, MU measurement unit
Full size table

Experiment 1

In subtask 1 of Experiment 1 we observed a reliable compatibility effect for numbers and measurement units. Participants’ RT were faster for compatible (predicted M = 1,102 ms, SE = 39 ms) trials with separate comparisons of numbers and measurement units biasing the same decision compared to incompatible trials with comparisons of numbers and measurement units biasing opposing decisions (predicted M = 1,166 ms, SE = 42 ms). Moreover, the reliable interaction between compatibility and digit distance indicated that the compatibility effect depended on digit distance. Estimated compatibility effects ranged from 27.47 ms (digit distance = 1) to 161.00 ms (digit distance = 8).

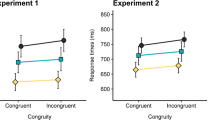
In subtask 2 of Experiment 1, all main effects as well as the interaction were significant. In addition to the significant compatibility effect, participants responded faster to string length congruent (predicted M = 962 ms, SE = 35 ms) as compared to string length incongruent items (predicted M = 1,006 ms, SE = 34 ms). Furthermore, the interaction between compatibility and string length congruity was significant indicating that the compatibility effect was larger in string length congruent than in incongruent trials (91 ms vs incongruent trials: 30 ms; see Fig. 1).

Fig. 1
figure 1

Estimated parameters of compatible/incompatible and string length congruent/incongruent trials. RT Reaction times. Error bars SE

Full size image

Experiment 2

Controlling for the holistic distance in Experiment 2, the compatibility effect was still present (compatible: predicted M = 1,102 ms, SE = 50 ms vs incompatible trials: predicted M = 1,186 ms, SE = 55 ms).

Experiment 3

We observed a reliable distance effect for scale units in Experiment 3 (see Fig. 2).

Fig. 2
figure 2

Black line Distance effect for measurement units in Experiment 3. Gray squares Empirical means, dashed lines lower and upper 95% confidence intervals (CI)

Full size image

Discussion

The present study set out to investigate the processing of measurement units. In particular, we hypothesized that processing of physical quantities can be explained by the model framework of generalized componential processing of multi-symbol numbers (Huber et al., 2014a). Indeed, our results were in well accordance with the model predictions. When string length was held constant, we observed that irrelevant numbers interfered with the processing of measurement units, resulting in a significant compatibility effect with prolonged RT and higher ER for incompatible trials. Moreover, in line with the finding of a larger unit-decade compatibility effect for large unit distances (Nuerk et al., 2001), the compatibility effect for physical quantities (i.e., numbers and measurement unit) depended on digit distance with larger compatibility effects for larger digit distances. Importantly, the compatibility effect was still present when controlling for holistic distance. Furthermore, responses were not only slower and more error prone for string length incongruent than congruent pairs but we also found the compatibility effect to be more pronounced for string length congruent trials. Finally, we observed a distance effect for measurement units, suggesting similar representations of the magnitudes reflected by numbers and measurement units. Thus, our results strongly corroborate the idea of a generalized model of componential multi-symbol number processing.

First, the presence of the compatibility effect clearly indicates componential processing of numbers and measurement units—complying with componential models of multi-digit number processing (see e.g., Ganor-Stern, Tzelgov, & Ellenbogen, 2007; Nuerk, Moeller, Klein, Willmes, & Fischer, 2011, for a review). Thereby, our results are hard to reconcile with the notion of an integrated holistic representation of numbers and measurement units in magnitude comparison tasks as suggested previously for two-digit numbers (e.g., Dehaene, Dupoux, & Mehler, 1990). Furthermore, the finding of such componential processing of physical quantities corresponds nicely with previous accounts of componential processing in arithmetic (e.g., Moeller, Klein, & Nuerk, 2011) as well as number line estimation (e.g., Moeller, Pixner, Kaufmann, & Nuerk, 2009).

Second, our results not only generalize multi-symbol compatibility effects to units of measurement but also allow transfer of the string length congruity effect found for decimal fractions to measurement units (Huber et al., 2014b). Thus, not only the number of digits, but also the number of characters (i.e., digits plus letters indicating the scale units) seems to be processed and compared separately.

Third, we found evidence for measurement units being represented similarly to digits. Most likely, measurement units are represented in ascending order (mm, cm, dm, and km) following a place coding scheme (Verguts, Fias, & Stevens, 2005). This finding also suggests that participants may “recycle” symbolic magnitude representations when processing measurement units. A similar account was suggested by Verguts and De Moor (2005) for single digit magnitudes in the case of two-digit numbers, and the processing of very large numbers in number line estimation (range: 1 thousand to 1 billion; Landy, Charlesworth, & Ottmar, 2014). Thus, participants seem to break down the processing of multi-symbol numbers (i.e., in most cases large numbers) into smaller more graspable units (i.e., their constituting components) as a fundamental organizational principle of the brain (Anderson, 2010).

The correspondence of the present pattern of results to previous findings on negative numbers (Huber et al., 2014a) and decimal fractions (Huber et al., 2014b) suggests that a common processing model might account for compatibility and the string length congruity effects. Using the model structure of Huber et al. (2014b) for conceptualizing physical quantities, we suggest separate processing pathways for numbers, measurement units, and the number of characters. Hence, we propose that there are separate (magnitude) representations for numbers, measurement units, and the number of characters that are activated concomitantly and compared to in parallel (i.e., numbers are compared with numbers, measurement units with measurement units, and the number of characters with the number of characters). The respective separate comparisons can lead to converging (compatible and/or string length congruent trials) or opposing (incompatible and/or string length incongruent trials) decision biases. Opposing decision biases result in a response conflict leading to prolonged RT and higher ER explaining the present findings.

Taken together, the present study corroborates the idea that a general model of componential multi-symbol number processing can account for the processing of a variety of multi-symbol numbers. In previous studies, we have shown that magnitude processing of natural numbers (see Nuerk et al., 2011 for a review), negative numbers (Huber et al., 2014a), and decimal fractions (Huber et al., 2014b) can be explained within this unified framework. In the present study, we extended the model framework to a widely neglected topic in numerical cognition, namely the processing of physical quantities, indicating that these can also be interpreted as an instance of multi-symbol numbers.