The perceived intensity of a stimulus depends on its context. Lighting a single candle generates a salient change in a dark room, but is barely noticed in a well-lit room. Weber’s law more precisely specifies this relationship—our ability to detect differences in a signal depends on the ratio between the difference and the signal’s baseline level. If a viewer is 75 % accurate at detecting a length difference between lines that are 2 and 2.2 cm in length, a proportionally larger difference would be needed to obtain the same level or performance for lines that are ten times longer: 20 and 22 cm. This ratio signature of Weber’s law has been observed across the perception of many continuous dimensions, such as length, weight, and the pitch of pure tones (Henmon, 1906).

There is controversy over whether the perception of numerosity is an exception to this law. Although Weber’s law states that discrimination should be noisy at all values, numerosity perception is near-perfect within its smallest baseline values. In a phenomenon called subitizing, previous studies have demonstrated that people can rapidly make nearly perfect counts of up to three to four objects (Jevons, 1871; Trick & Pylyshyn, 1994). In one of the first demonstrations of subitizing, Jevons threw handfuls of beans across a table, each time making an immediate count of the subset that landed in a small tray. His performance was perfect for one to four beans, with only a few errors for five beans, and then consistently high error for six to 16 beans. Since this first demonstration, subitizing has been widely observed across a variety of studies (e.g., Kaufman, Lord, Reese & Volkmann, 1949; Trick & Pylyshyn, 1994).

This evidence of high precision for small collections does not necessarily mean that numerosity violates Weber’s law (Dehaene, 2003). People can estimate number within collections of any size, but as predicted by Weber’s Law, with a level of error proportional to the number of objects (Gallistel & Gelman, 1991; Whalen, Gallistel & Gelman, 1999). This proportional level of precision may extend down through the smallest collections, but a special property of numerosity may make this proportional noise hard to detect. Unlike the continuous dimensions of length, weight, and pitch, number is discrete, setting a minimum value of 1 on the size of between-collection differences that can be presented. This minimum difference of 1 unit may be sufficiently large to mask any uncertainty about number judgments within small (e.g., one to three) collections, yet also small enough to prevent confident discrimination among larger (e.g., four or more) collections.

An account that explains subitizing through the interaction of proportionally scaled noise masked by a minimum difference value between numbers (one unit) has the advantage of parsimony over those claiming special status for small collections. It also has empirical support, as some measures have suggested proportional “mental spacing” even for small collections. When discriminating between small collections, response times slowed for smaller ratios, consistent with Weber’s law (e.g., 1:2, 2:3, 3:4; Lemmon, 1927). Response times were invariant, however, for discriminations between collections with different “baselines” but a constant ratio (1:2, 2:4, 3:6; Crossman, 1955). In another study, participants arranged cards containing visual dot patterns into equally psychologically spaced categories, and their responses reflected ratio spacing even across small collections of objects (Buckley & Gillman, 1974).

Yet also, some evidence supports the alternative interpretation that the perception of numerosity in small collections is “superprecise” relative to the predictions from Weber’s law. Such superprecision could stem from special processing mechanisms that are available to the visual system for small collections. Evidence for these special mechanisms has stemmed from suspiciously consistent capacity limitations of three to four objects or locations (for a discussion, see Franconeri, Alvarez & Enns, 2007) across phenomena such as object tracking (Pylyshyn & Storm, 1988) and visual memory (Luck & Vogel, 1997). Studies on infants have provided particularly powerful evidence of the special processing of small collections. For example, infants can discriminate two objects from three, but not one object from four, suggesting that small and large collections (for infants, four appears to be a ‘large’ collection) may rely on incompatible representations (Feigenson, 2007). Therefore, determining whether small-collection enumeration is truly superprecise holds strong implications for how we understand the capacity limits on the visual system, as well as for the human ability to differentiate discrete objects from continuous substances (Hespos, Ferry & Rips, 2009) and the developmental mechanism that bootstraps our understanding of number (Carey, 2010).

How could the accounts above be dissociated? One possibility would be to model the precision of the estimation process and to evaluate fits for the competing accounts. But one such analysis failed to find satisfactory fits to performance for versions of both the Weber’s law and “special-mechanism” accounts (Balakrishnan & Ashby, 1991), suggesting that modeling may not be the most fruitful route. One possibility would be to compare identical ratios at different baselines (e.g., 2:3 vs. 20:30) at which Weber’s law predicts identical performance. The first study to use this approach revealed perfect correspondence with Weber’s law (Crossman, 1955). However, this study used a high ratio of 1:2, leaving strong potential for performance ceiling limitations. In the present study, we will use a wider range of ratios.

Another study featured a comprehensive range from one to eight and ten to 80 objects, comparing naming times and accuracy (Revkin, Piazza, Izard, Cohen & Dehaene, 2008). Small collections of one to four showed near-perfect counts, in contrast to the difficultly with large collections of ten to 40. However, this relative advantage for small collections could have stemmed from postperceptual stages of the task. In particular, the advantage could stem from strong existing mappings from perceptual information related to number, due to verbal labels for those numbers. The participants had a lifetime of practice with the verbal labeling of small collections (i.e., linguistic frequencies dramatically decrease with numerosity intensity; Dehaene & Mehler, 1992), as compared to limited training with the naming of larger collections. Linguistic frequency relationships might underlie other effects that ostensibly reflect the structure of number representations (e.g., the SNARC effect; Hutchinson, Johnson & Louwerse, 2011) and can serve as a proxy for distance relationships more generally—indeed, a map of Middle Earth can be generated solely from the co-occurrence of geographic locations in the text of The Lord of the Rings (Louwerse & Benesh, 2012).

Here, we isolated the perceptual limits of enumeration by using a visual comparison task that did not require verbal labeling. In this way, we were able to show conclusively that the enumeration of small collections is perceptually superprecise relative to the predictions of Weber’s law.

Experiment 1

Observers judged the relative numerosities of collections with either small (3 vs. 1, 2, 4, or 5) or large (30 vs. 10, 20, 40, or 50) baselines. Weber’s law predicts that performance should be identical across these baselines, as long as the ratios are equal. If Weber’s law were violated, response times (RTs) should be faster for comparisons of 1:3 and 2:3, relative to 10:30 and 20:30, respectively. Such advantages may only be present for 2:3 relative to 20:30 because the smaller ratio creates a difficult comparison. This advantage would manifest as an interaction between baseline size and ratio size within the lower values in each baseline size. If such differences were absent in the higher values of each baseline (3:4, 3:5; 30:40, 30:50), it would point even more definitively to superprecision in the range from one to three (marked by a triple interaction between baseline size, ratio size, and comparison direction).

Methods

Participants

A group of 25 Northwestern undergraduates (15 females, 10 males) participated in this experiment. All of the participants were naive and reported corrected-to-normal vision. To ensure that all participants could “subitize,” they also performed a separate number-naming taskFootnote 1 after the experiment, and one participant (male) was excluded from further analysis due to accuracy rates lower than 90 % for collections of one to three objects.

Stimuli and apparatus

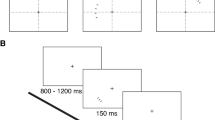
All of the stimuli were created and displayed using MATLAB with the Psychophysics Toolbox (Brainard, 1997; Pelli, 1997) on an Intel Macintosh running OS X 10.6. All stimuli were displayed on a 17-in. ViewSonicE70fB CRT monitor (1,024 × 786, 75 Hz). The viewing distance was approximately 57 cm. In a fixation display, a green (91 cd/m2) bar with a size of 0.29° (width) × 21.43° (height) appeared for 200 ms on a black background (42 cd/m2). The subsequent dot collection display (see Fig. 1) added two collections (white 101-cd/m2 dots, each subtending 0.30°) scattered within imaginary circles (11° diameter) with center points 8.93° to the left and right of fixation. One collection always had 3 or 30 dots, and the other collection either 1, 2, 4, or 5 or 10, 20, 40, or 50 dots. The dots were randomized without overlap by choosing 198 random locations, with an additional random jitter ranging from 0° to 0.14°.

Fig. 1
figure 1

Four schematic dot displays used in Experiments 1 and 2. The ratios printed at the bottom right comer of each example display were not displayed during the experiments. A fixation was presented for 200 ms, with a 100-ms beep. Then, a dot display was presented until response. The size of the baselines and the location of the reference collection (always three or 30 dots) were blocked, and the block order was counterbalanced across participants

Full size image

Procedure

Participants reported whether the variably sized collection contained fewer or more dots than the reference (3 or 30). The baseline size order was blocked across participants with an ABAB or BABA counterbalancing, and the location of the reference collection was blocked as AABB or BBAA (Fig. 1). Each trial began with a 100-ms beep simultaneous with a 200-ms fixation display, and then the dot collection display was presented until response. Each variably sized collection (e.g., 1, 2, 4, or 5) was equally likely within a block. Participants pressed keys labeled “more” or “fewer” in order to make relative judgments, with the label mapping being counterbalanced to the “k” and “o” keys across participants. Errors resulted in feedback (the word INCORRECT presented for 2,500 ms). The intertrial interval (ITI) was 800 ms. The total number of trials was 288: 2 baseline sizes (3 or 30) × 2 ratio sizes (larger [1:3, 3:5] or smaller [2:3, 4:5]) × 2 comparison directions (fewer or more) × 2 reference collection locations (left or right) × 18 repetitions.Footnote 2 The experiment lasted approximately 30 min, including 16 practice trials and the subsequent number-naming task.

Results and discussion

For each participant, RTs higher than three SDs over the mean were discarded, as well as an equal number from the opposite side of the distribution (M = 4.3 %, SD = 1.3 %). The average accuracy was 94.6 % (SD = 2.6 %). The patterns of error rates qualitatively matched the RT data.

The RTs for correct trials were entered into a repeated measures ANOVA with three factors: Baseline Size (small vs. large), Comparison Direction (fewer vs. more), and Ratio Size (smaller vs. larger) (see Fig. 2a). The RT for small-baseline-size collections (M = 561 ms, SE = 17 ms) was not significantly faster than the one for large-baseline collections (M = 573 ms, SE = 20 ms), F(1, 23) = 2.9, p = .10, η 2 = .11. The RT was faster for the “fewer” (M = 551 ms, SE = 18 ms) than for the “more” (M = 583 ms, SE = 19 ms) comparison direction, F(1, 23) = 17.1, p < .001, η 2 = .43, and the RT was also faster for larger (M = 540 ms, SE = 17 ms) than for smaller (M = 594 ms, SE = 20 ms) ratio sizes, F(1, 23) = 134.9, p < .001, η 2 = .85. These results are both consistent with the idea that smaller target-to-reference ratios can increase the difficulty of number comparisons.

Fig. 2
figure 2

Average response times (RTs) and error rates for Experiments 1 and 2 for both the small-baseline (×1) and large-baseline (×10) collections. Filled circles connected by solid lines represent the small-baseline condition (one to five), and open circles connected by dashed lines represent the large-baseline condition (10–50). Average error rates are also shown with the RTs; black bars represent the small-baseline condition, and white bars represents the large-baseline condition. Error bars depict standard errors

Full size image

Critically, baseline size interacted significantly with each of the other two factors: Baseline Size × Comparison Direction, F(1, 23) = 5.9, p = .02, η 2 = .20; Baseline Size × Ratio Size, F(1, 23) = 15.6, p < .001, η 2 = .40; and most importantly, Baseline Size × Ratio Size × Comparison Direction, F(1, 23) = 8.7, p = .007, η 2 = .27. This predicted three-way interaction shows that 20:30 comparisons were slower than 10:30 comparisons by 91 ms (SE = 7 ms), but that such distance effects were smaller between the 1:3 and 2:3 comparisons, at 45 ms (SE = 6 ms). This three-way interaction also shows that the distance effect difference was not present outside of the subitizing range: The 30:40 comparisons were slower than the 30:50 comparisons by 44 ms (SE = 5 ms), and the difference in the distance effect was comparable between 3:4 and 3:5, at 36 ms (SE = 6 ms). Figure 3 depicts this three-way interaction in a more straightforward format, showing the large increase in precision for “fewer,” but not for “more,” judgments of small collections. These results suggest that small collections of one to three are superprecise, in contrast to Weber’s law.

Fig. 3
figure 3

Differences in the slopes between the small-baseline condition (solid lines) and the large-baseline condition (dashed lines) from Fig. 2 (a proxy for each of the two-way interactions visible in that figure), represented as bars showing single values. If enumeration is based on Weber’s law, these values should not deviate from zero, because distance effects should be equal for the large- and small-baseline judgments. In contrast, distance effects were far smaller in small-baseline judgments for “fewer” judgments, in both Experiments 1 and 2. These patterns plotted above together suggest a superprecise enumeration for collections of one to three objects, well beyond the precision predicted by Weber’s law

Full size image

Experiment 2

In Experiment 2, we replicated these effects using a second type of comparative judgment: Instead of reporting “more” or “fewer,” we asked participants to report “same” or “different.” The patterns of RTs and accuracy for the different trials reflected the same critical three-way interaction found in Experiment 1.

Method

Participants

A group of 28 Northwestern undergraduates (14 females, 14 males) participated in Experiment 2. All participants reported normal or corrected-to-normal vision and were naive to the purpose of this experiment. The same number-naming control task was used, leading to the exclusion of four participants (two males, two females) who could not perform at 90 % at rapid number naming for small collections (one to three objects).

Stimuli and apparatus

These were identical to those aspects of Experiment 1.

Procedure

The procedure was identical to that of Experiment 1, except for the following changes. The task was to judge whether the two collections had either the same or different numbers of dots. In addition to the displays with different numbers of dots, an equal frequency of same trials was added in which both collections had either three or 30 dots. The experiment consisted of 384 same trials [2 baseline sizes (3 vs. 30) × 192 repetitions] and 384 different trials [2 baseline sizes (3 vs. 30) × 2 comparison directions (more vs. fewer) × 2 ratio sizes (larger vs. smaller) × 2 reference collection locations (left vs. right) × 24 repetitions]. Experiment 2 lasted about 50 min, including 16 practice trials and the subsequent number-naming task.

Results and discussion

Using the same screening procedure as in Experiment 1, we discarded 3.1 % of the trials (SD = 1.0 %). The average accuracy of the remaining trials was 84.0 % (SD = 19.96 %). The patterns of error rates qualitatively matched the RT data.

For the different trials, the same ANOVA as in Experiment 1 again revealed that RTs were significantly faster in the “fewer” comparison direction (M = 696 ms, SE = 15 ms) than in the “more” comparison direction (M = 766 ms, SE = 18 ms), F(1, 23) = 17.1, p < .001, η 2 = .43. RTs were also faster for larger (M = 695 ms, SE = 15 ms) than for smaller (M = 768 ms, SE = 18 ms) ratios, F(1, 23) = 134.9, p < .001, η 2 = .85 (see Fig. 2b). Unlike in Experiment 1, we found a strong effect of baseline size, F(1, 23) = 72.2, p < .001, η 2 = .76 (small, M = 652 ms, SE = 15 ms; large, M = 811 ms, SE = 22 ms). A similar effect was present in the same trials, in which the average RT was slower for the large baseline (M = 823 ms, SE = 14 ms) than for the small baseline (M = 642 ms, SE = 11 ms), t(23) = 7.6, p  .001. The main effect of baseline size may have occurred because the same–different discrimination task in Experiment 2 entailed more fine-grained decision thresholds around the neighboring responses: “Same–different” decisions require discrimination between smaller ratios—for example, among 2:3/20:30, 3:3/30:30, and 3:4/30:40—than do “more–fewer” decisions—between 2:3/20:30 and 3:4/30:40. Most importantly, baseline size interacted with all of the other main factors: Baseline Size × Comparison Direction, F(1, 23) = 19.6, p < .001, η 2 = .46; and Baseline Size × Ratio Size, F(1, 23) = 29.8, p < .001, η 2 = .56. The three-way interaction of Baseline Size × Ratio Size × Comparison Direction was again significant, F(1, 23) = 24.0, p < .001, η 2 = .51, showing that the size of distance effects was reduced only for relative judgments on one to three objects, but not for relative judgments on three to five objects, as compared with their matched large collections (see Fig. 3).

General discussion

Our results suggest that number discrimination in small collections of one to three objects is visually more precise than is predicted by Weber’s law. If the precision of each collection’s number representation were indeed proportional to its value, number discriminations between small collections (e.g., 2:3) should have shown performance equal to that in larger discriminations with the same ratio (e.g., 20:30). Instead, RTs for decisions about the small collections were far faster than those for large collections, both for relative numerosity discrimination (Exp. 1) and for same–different numerosity discrimination (Exp. 2). To our knowledge, these results are the first demonstration that small-collection “superprecision” is indeed rooted in the visual stages of numerosity judgment, isolating this precision from later stages that associate those representations with symbolic or verbal codes.

Where does this superprecision come from? We know of two classes of explanation that remain if the Weber’s law explanation is ruled out. The first is that the diagnostic value of visual information across small collections is inherently higher than for large collections. Number perception may rely on correlations between number and other visual features, such as a collection’s covered area (e.g., the group’s circumference), textural density, spatial frequency profile, or other operations over primitive image segmentation (see Franconeri, Bemis & Alvarez, 2009, for a discussion). For example, a change from one dot to two dots causes powerful changes to the spatial frequency profile of a collection. Changing from two to three dots causes an equally powerful difference to the second spatial dimension of this spatial frequency profile (since the original two dots could only be arranged in a single spatial dimension).

Consistent with this idea, adding additional objects in a linear arrangement makes subitizing abilities vanish (Allen & McGeorge, 2008). Critically, for large collections, changes of the same ratio sizes, such as 10:20 or 20:30, create nowhere near the same magnitude of signal difference among these dimensions. A collection of 20 essentially fills an entire display or container, and a collection of 30 adds little more surface area or difference in the spatial frequency profile. Such cues may be the reason why participants rate individual numerosities as being similar to each other (e.g., three-object patterns all look similar), but different from flanking values (e.g., three-object patterns look dissimilar from four-object patterns). These patterns reverse for larger collections—the similarity among seven-object patterns disappears, so that seven starts to look similar to eight (Logan & Zbrodoff, 2003).

A second class of explanation is that something special about the architecture of the visual system outputs discrete value for each small collection of one to three objects. For example, the perception of small collections may tap a shape recognition system that treats dots or objects as the vertices of a polygon, yielding long-term memory associations between those shapes and the number or vertices (or sides) that they contain (Mandler & Shebo, 1982). A dot entails one object, a line two, a triangle three, and a square or diamond four. Larger numbers do not signal prototypical shapes, and therefore should not produce efficient performance. The disruption of subitizing by linear arrangement has been used to support this account, because shape is also disrupted (Allen & McGeorge, 2008). And subitizing limits can be raised when patterns signal familiar shapes (Peterson & Simon, 2000), such as dice patterns (Mandler & Shebo, 1982).

Another possibility is that the visual system may contain an object individuation mechanism that is limited to three to four objects (Trick & Pylyshyn, 1994), which could rise from limitations in the cortical spacing of objects (Franconeri, Alvarez & Cavanagh, 2013; Franconeri, Jonathan & Scimeca, 2010). The most compelling evidence for this possibility comes from a surprisingly clear trade-off between performance in a multiple-object tracking task and a concurrent subitizing task: While attentively tracking multiple moving objects, subitizing limits decreased by one for each additional object tracked (Chesney & Haladjian, 2011). A similar trade-off was also found between a visual memory task and a concurrent subitizing task, but not between the visual memory task and concurrent numerosity judgments on large collections (Piazza, Fumarolar, Chinello & Melcher, 2011). Similarly, subitizing was significantly compromised under attention-demanding concurrent tasks (Olivers & Watson, 2008; Railo, Koivisto, Revonsuo & Hannulae, 2008), in which some common processing resource may have been recruited for individuation (Intriligator & Cavanagh, 2001). Subitizing limits might also decrease if collections are cramped in a rather smaller cortical space—for example, within a visual quadrant—thus hindering efficient individuation (Delvenne, Castronovo, Demeyere & Humphreys, 2011).