The number line task is often used to assess children’s and adults’ underlying representations of integers (e.g., Berteletti, Lucangeli, Piazza, Dehaene, & Zorzi, 2010; Geary, Hoard, Nugent, & Byrd-Craven, 2008; Opfer & DeVries, 2007; Siegler & Booth, 2004; Siegler & Opfer, 2003). The traditional task consists of a bounded number line with labeled endpoints (e.g., 0–100) and a target number. On each trial, the participant is asked to indicate the position on the number line that the target number would occupy. Bounded number line tasks, however, have limitations (see, e.g., Barth & Paladino, 2011). Here, we (1) demonstrate that the bounded number line task is an invalid measure of integer representation, (2) present a new task, an unbounded number line task, that overcomes the limitations of the bounded number line and produces data consistent with integer representation, and (3) present a preliminary description of adults’ underlying representation of integers, using the unbounded number line data.

One’s intuitive understanding of an integer (also referred to as an analogue quantity representation or analogue magnitude) can be described as a distribution of quantities. For example, each time we see 15, we understand its quantity to be slightly different (sometimes greater than 15, sometimes less). The distribution of quantities one associates with an integer describes one’s psychological understanding of that integer. There is much debate in the literature concerning the placement and variance of these psychological distributions in relation to each other. The debate concerns whether integers are best described by a psychological representation in which (1) the mean distances between successive integers are logarithmically spaced and the perceptual errors associated with successive integers have a fixed variance (logarithmic models; e.g., Banks & Hill, 1974; Dehaene, 2003; Dehaene, Dupoux, & Mehler, 1990; Nieder & Miller, 2003), or (2) the mean distances between successive integers are linearly spaced and the perceptual errors associated with successive integers have scalar variance (i.e., linear models, with variance increasing with successive integers; e.g., Gibbon, 1977; Gibbon & Church, 1981; Meck & Church, 1983; Whalen, Gallistel, & Gelman, 1999).

Using the number line task, Siegler and Opfer (2003) showed that younger children produced a negatively accelerating error pattern (e.g., logarithmic). Older children and adults, in contrast, produced more linear estimates. The authors concluded that there was a gradual shift from logarithmic to linear representations of integers. This effect has been well replicated and generalized to include both more age groups and participants with varying mathematical abilities (e.g., Berteletti et al., 2010; Booth & Siegler, 2006; Geary et al., 2008; Laski & Siegler, 2007; Siegler & Booth, 2004; Thompson & Opfer, 2008).

Barth and Paladino (2011) have reinterpreted the number line data, suggesting that the apparent linearity in children’s number line data is actually the ogival pattern typical of a proportion estimation strategy (for a review of proportion estimation, see Cohen, Ferrell, & Johnson, 2002).Footnote 1 Specifically, stimulus bias often follows Stevens’s power law,

$$ \psi (I) = k{I^a}, $$
(1)

where I represents the stimulus intensity, k is a constant, and a is the characteristic exponent, which describes the observer’s stimulus bias. Exponents greater than 1 indicate a positively accelerating bias (e.g., exponential), and exponents less than 1 indicate a negatively accelerating bias (e.g., logarithmic). Data from traditional number line tasks are typically interpreted within the framework of Stevens’s power law. However, when viewed closely, number line data appear more ogival than linear or accelerating. The ogival error pattern is emblematic of proportion estimation tasks, in which observers are presented with a whole and asked to estimate a fraction of that whole, say 20%. Spence (1990) discovered that observers tend to estimate a target proportion in relation to the whole. Spence adapted Stevens’s power law to model this process (termed the power model). Spence’s power model predicts that observers will be accurate at both the boundaries and the halfway point, with perceptual bias manifesting as the signature ogival pattern. Hollands and Dyre (2000) expanded Spence’s power model to describe the use of multiple reference points (termed the cyclic power model, here abbreviated CPM). CPM predicts multiple cycles of the ogival pattern, depending on the number of reference points the observer adopts.

The number line task can be conceptualized as a proportion estimation task because the labeled endpoints reveal the value of the whole. To accurately complete the task, integers smaller than the whole must be converted to proportions of that whole (e.g., 50 is halfway between 0 and 100), rather than directly estimated as integers (e.g., 50 is 50 units to the right). Barth and Paladino (2011) showed that the CPM accurately predicts 7-year-olds’ bias in the bounded number line task and concluded that children conceptualize the bounded number line task as a proportion estimation task. Because the relation between the cognitive processes underpinning one’s understanding of proportions and integers is unclear (e.g., Cohen, 2010), one cannot assume that the data from the bounded number line task adequately describe integer representation.

The limitations of the bounded number line task extend beyond its similarity to a proportion estimation task. Specifically, the lower and upper bounds limit the degree and direction of possible error in the task. The lower bound limits one’s ability to underestimate small values, and the upper bound limits one’s ability to overestimate large values. Thus, the bounded number line task is likely an invalid measure of estimation variability. Estimation variability is of central importance to theories of numerical cognition (e.g., as discussed above, logarithmic models often posit fixed variance, and linear models often posit scalar variance).

Here, we present a new task, an “unbounded number line” task, which does not have the limitations of the bounded number line task. Experiment 1 assessed adults’ bias on a bounded number line task. To assess whether the adults treated the bounded number line task as a proportion estimation task or as an integer estimation task, we fit both a linear model and the CPM to each participant’s data, as well as analyzed the error data. Experiment 2 assessed adults’ bias on our new, unbounded number line task, in which we displayed the distance between 0 and 1 and asked participants to indicate the location of their estimate to the right of the presented unit. To assess the adults’ strategy, we fit both a linear model and a new, nonlinear “scalloped power model” to each participant’s data, as well as analyzing error data.

Experiment 1

Method

Participants

Fifty-two undergraduates from an introductory psychology class volunteered in exchange for course credit.

Apparatus and stimuli

All stimuli were presented on 24-in. LED color monitors with 72-Hz refresh rates controlled by a Mac mini. The resolution of the monitor was 1,920 × 1,200 pixels. Participants sat approximately 30 in. away from the screen.

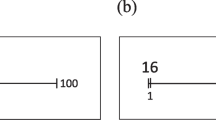
On each trial, participants were presented with a number line and target number (see Fig. 1). The number line was centered on the y-axis of the screen. The target number was placed half an inch below the left boundary of the number line. The number line was constructed from 1-pixel-thick red lines, with a 10-pixel-high vertical line marking the start of the number line. This left boundary was labeled with the number “0.” A similar vertical line indicated the right end of the number line and was labeled with the number “26.” The two vertical lines were connected at the bottom by a red horizontal line (i.e., the number line). The target numbers ranged from 2 to 25 and were chosen randomly from a uniform distribution from trial to trial.

Fig. 1
figure 1

Methods and results of Experiment 1, using the bounded number line task. The image at the top represents the means by which participants estimated the location of the target number (shown here as X) on the bounded number line. The black lines in this top panel indicate the stimulus presented, and the gray solid line indicates the line revealed on the “click and drag.” The hand represents the cursor, and the gray dashed arrow indicates movement. Below the number line are examples of participants who were best fit by the linear model, the one-cycle CPM, and the two-cycle CPM. The bottom graph represents the relationship between the standard deviations of the estimates and the target number. The standard deviation is lower for target numbers near reference points and higher for target numbers between reference points

Full size image

To prevent participants from using reference points external to the number line (e.g., the position of the left edge of the monitor or the center of the monitor), we varied the location and physical length of the number line. For each trial, the number line was randomly placed between 100 and 200 pixels from the left side of the screen. The length of the number line was also randomly varied from 52 to 832 pixels. In addition, we placed a strip of black tape across the bottom of the monitor to conceal the reflective Apple symbol.

Procedure

The experiment took place in individual dark rooms. The participants were instructed to estimate the appropriate position of the quantity indicated by a target number on the number line. To do this, participants used a mouse to “click and drag” the left boundary line to the estimated target location. To click and drag, the participant moved the cursor over the left boundary line. At that point, a gray line appeared covering the left red boundary line. The participant then pressed the left mouse button and dragged the gray line to the estimated target location. As the gray line was dragged, the left red boundary line remained in place. Participants could freely move the gray line, dragging and releasing without submitting a response. When the participant determined that the placement of the target line was accurate, he or she pressed the space bar to submit the response. The next trial appeared 1 s after the submission of the response. Participants’ accuracy, to the pixel, and reaction time (RT) were recorded.

Each participant was presented with 3 practice trials and 400 experimental trials. The participants had a self-timed break every 101 trials. The experiment typically lasted under 1 h.

Results

We removed all estimates in which the participants’ RTs were greater than 45 s or less than 500 ms. Estimates over three standard deviations from the mean error for each target number (i.e., under 25% or over 150% of the target number) were also removed. These constraints eliminated 2.6% of the data.

We calculated the mean estimate of each target number from all trials for each participant. We then tested the fit of three models using generalized nonlinear least squares (gnls) methods. The models used were linear,Footnote 2 CPM with two reference points (i.e., the bounds of the number line), and CPM with three reference points (i.e., the bounds and the midpoint of the number line)Footnote 3 (see Hollands & Dyre, 2000).

Each participant was categorized as being linear, two-point CPM, or three-point CPM on the basis of the Akaike information criterion (AIC) goodness-of-fit measure. We assessed the global appropriateness of the models by the model that fit the majority of participants. Seven participants were determined to be linear, 32 fit the two-point CPM, and 13 fit the three-point CPM. Thus, 87% of the participants were best classified by the CPM. The critical exponent, describing the numerical bias, for the CPM (M = 1.13, SD = 0.14) was significantly different from 1, t(44) = 6.3, p < .01. The intercept of the linear model was –1.1 and significantly different from 0, t(6) = –7.46, p < .01. The slope was 1.03 and approached being a significant difference from 1, t(6) = 2.17, p = .06. The r 2 of all models was over .99. Figure 1 shows data for some of the participants whose data were best predicted by each of the three models.

The bottom panel of Fig. 1 plots the participants’ average standard deviations as a function of target number. The average standard deviation is lower at the reference points and increases between the reference points. This pattern is consistent with a proportion estimation strategy, rather than an integer estimation strategy.

Discussion

We applied the CPM to the number line task in order to assess numerical bias. The majority (87%) of the participants’ data were better fit by the CPM than by the linear model. This indicates that adults treat the bounded number line task as a proportion estimation task. Adults’ estimates are described by a positively accelerating bias, revealing that the subjective distance between successive numbers increases as the target number increases. We will discuss this finding in detail in the General Discussion.

In an attempt to remove the proportion estimation strategy used by most participants in Experiment 1, we conducted Experiment 2.

Experiment 2

Method

Participants

Fifty-two naïve undergraduates from an introductory psychology class volunteered in exchange for course credit.

Apparatus and stimuli

The unbounded number line differs from the bounded number line in two ways. First, the unbounded number line only represents a single, unit distance; here, we used 0 to 1. Second, estimations are made external to the bounds rather than within them.

For each trial, participants were presented with the unbounded number line and a target number (see Fig. 2). The left and right boundaries were unlabeled vertical lines.Footnote 4 The vertical lines were connected at the bottom by a horizontal line, the length of which represented the distance of one unit. Centered directly below the unit was the label “1.” The target number was presented below the label.

Fig. 2
figure 2

Methods and results of Experiment 2, using the unbounded number line task. The image at the top represents the means by which participants estimated the location of the target number (shown here as X) beyond the presented unit. The black lines in this top panel indicate the stimulus presented, and the gray solid lines indicate the lines revealed on the “click and drag.” The hand represents the cursor, and the gray dashed arrow indicates movement. Below the number line are examples of participants who were best fit by the linear, dual-scallop, and multi-scallop models. The bottom left graph represents the increase in the standard deviations of estimates with the target number. The bottom right graph shows standard deviation as a constant proportion of target numbers greater than 5

Full size image

The location of the number line varied just as in Experiment 1. However, the length of the number line was randomly varied from 2 to 32 pixels long. These distances match the smallest and largest single-unit sizes from Experiment 1. Although estimates were not limited by the boundaries of the number line, estimates could not be closer than 100 pixels to the right edge of the screen. This provided sufficient room for participants to overestimate the largest target number with the largest unit size by 200%.

Procedure

The same rooms and computers were used as in Experiment 1. Participants were informed that the presented lines were the start of a number line and represented one unit. Their task was to estimate the position of a target number to the right of the number line for each trial. To do this, they clicked and dragged the right boundary line to the estimated target location. The same click-and-drag method used in Experiment 1 was used here. So, if the target number was 10, participants were to drag the line nine units to the right, so that the rightmost boundary would be located ten units to the right of the leftmost boundary of the number line. In all other respects, the procedure of Experiment 2 was identical to that of Experiment 1.

Results

As in Experiment 1, trials with RTs of more than 45 s or less than 500 ms were removed. Estimates over three standard deviations from the mean error for each target number (i.e., under 25% or over 480% of the target number) were also removed. These constraints eliminated 3.5% of the data. Finally, we removed the participants’ responses to the target numbers 23–25 because the computer screen boundary acted as an artificial endpoint and skewed these data low. That is, the error associated with participants’ average responses was greater than we anticipated, and the edge of the computer screen interfered with the participants’ estimates of the larger target numbers.

Because the unbounded number line task was designed to inhibit the participants’ proportion estimation strategy and because there was little evidence of an ogival pattern in these new participants’ data, we believe that we successfully inhibited the participants’ use of a proportion estimation strategy. Nevertheless, participants instead tended to adopt a dead-reckoning strategy. We identified the dead-reckoning strategy on the basis of verbal reports by pilot participants and tested the validity of this hypothesized strategy by developing a model and assessing its fit. In this dead-reckoning strategy, participants first moved a unit on the number line, then estimated the position of the next unit based on their current position, and so on. This dead-reckoning strategy is often revealed by a repetitive scalloped pattern of errors in the data (see Fig. 3). This scalloped pattern results when participants use multiples of a small quantity (about ten) to estimate their position on the number line. We term this range the participants’ working window of numbers. When participants are asked to estimate numbers above this range, they count to the last number in their working window, say ten, and from that endpoint they start counting from one again. For example, if the target number was 12, a participant might estimate the location of ten, then estimate two more units. This creates a scalloped pattern in the data, revealing a repeating bias. We had three classes of participants: (1) those who estimated numbers directly (single scallop), (2) those who repeated their bias twice (dual scallop), and (3) those who repeated their bias multiple times (multiscallop). The mathematical formulas for this scallop power model (SPM) are below:

$$ \begin{array}{*{20}{c}} {Y = {X^b},} & {\hbox{Single Scallop}} \\\end{array} $$
(2)
$$ \begin{array}{*{20}{c}} {{\hbox{if}}\left( {X < d} \right){\hbox{then}}\left( {Y = {X^b}} \right){\hbox{else}}\left( {Y = {d^b} + {{\left( {X - d} \right)}^b}} \right),} & {\hbox{Dual Scallop}} \\\end{array} $$
(3)
$$ \begin{array}{*{20}{c}} {Y = {\hbox{truncate}}\left( {X/d,0} \right) \cdot {d^b} + {{\left( {X\,{\hbox{modulo}}\,d} \right)}^b},} & {\hbox{Multiscallop}} \\\end{array} $$
(4)

where X is the target number, b is the characteristic exponent, and d is the size of the working window.

Fig. 3
figure 3

Example of the dead-reckoning strategy used by most participants in the unbounded number line task. The points represent average estimates of the location of the target number for a single participant. The gray lines represent the repeated pattern of error. The curvature of the error is described by b, the bias, and the extent of the biased segment is described by d, the size of the working window of numbers. In this example, the working window is about five units wide, and the bias is a characteristic exponent greater than 1

Full size image

For each participant, we calculated the mean estimate of each target number from all trials. We then tested the fit of the four models using gnls methods. The models used were linear, single-scallop, dual-scallop, and multiscallop models. Each participant was categorized into a best-fit model on the basis of the AIC goodness-of-fit measure. We assessed the global appropriateness of the models by identifying the model that fit the majority of participants. Four of the participants were determined to be linear, 20 fit the single-scallop model, 16 fit the dual-scallop model, and 12 fit the multiscallop model. Thus, 92% of the participants were best classified by the SPM. The critical exponent, describing the numerical bias, of the SPM (M = 1.11, SD = 0.2) was significantly different from 1, t(47) = 3.4, p < .01. The working window averaged 10.6 for the SPMs that included that parameter (dual and multi). The average intercept of the linear model was –1.21, and the average slope was 1.56. Because there were only four linear observations, we did not assess significance. The r 2 averaged .95 for the SPM and .975 for the linear model. Figure 2 shows data for some of the participants whose data were best predicted by each of the models.

The bottom panels of Fig. 2 plot participants’ average standard deviations as a function of target number. The average standard deviation increased with target number, such that error variance was a constant proportion of the target number for all numbers greater than five. This pattern is consistent with scalar variance (Gibbon, 1977).

Discussion

As in Experiment 1, participants showed a positively accelerating numerical bias. Unlike Experiment 1, however, participants’ errors increased to scalar variance for quantities from 2 to 5 and remained stable at scalar variance for quantities greater than five. We discuss these results below.

General discussion

In Experiment 1, we presented participants with a bounded number line task similar to that used by Siegler and Opfer (2003) and their colleagues. Our results showed that adults use a proportion estimation strategy that makes their biased estimates appear linear. In Experiment 2, we presented participants with an unbounded number line task that successfully eliminated the use of a proportion estimation strategy. Both Experiment 1 and 2 revealed an accelerating power function of numerical bias. Furthermore, whereas the error variance in the bounded number line task was suppressed by the bounds, a scalar variance error pattern was present in the unbounded number line task. The present data suggest that both tasks are tapping into the same underlying numerical cognition structure, but the error data suggest that the unbounded number line task is a more pure measure of integer representation.

The number line task is often used to assess the psychological representation of integers. The psychological representation of each integer (ψ i ) can be described by the relative placement (m i ) and variance (σ i ) of the psychological distribution describing our understanding of that integer’s quantity:

$$ {\psi_i}\left( {{m_i},{s_i}} \right). $$
(5)

Perceived mean distance is the psychological construct associated with the mean distance between the psychological distributions representing successive integers on a psychological number line:

$$ \left( {{m_i} - {m_i}_{{ - {1}}}} \right). $$
(6)

Perceived mean distance provides an understanding of the layout of our psychological number line, but alone it provides no information about how well people can distinguish two successive integers. Both the bounded and unbounded number line tasks reveal a positively accelerating power function describing the perceived mean distance between successive integers. This result was unexpected, because no major theory makes such a prediction. Nevertheless, very few empirical studies have assessed perceived mean distance without using the bounded number line.Footnote 5 As a result, little is known about the perceived mean distance between integers. Our data provide a striking new piece of evidence that can help further our understanding of the placement of integers on the psychological number line.

Most empirical studies addressing numerical bias have assessed perceived difference, which can be conceptualized as the amount of overlap of the psychological distributions associated with two successive integers and can be formalized by the following formula:

$$ \frac{{\left( {{\mu_i} - {\mu_{{i - 1}}}} \right)}}{{\frac{{\left( {{\sigma_i} + {\sigma_{{i - 1}}}} \right)}}{2}}} $$
(7)

Perceived difference provides an understanding of how well people can distinguish two successive integers. Two integers with distributions that greatly overlap (a small perceived difference) are more difficult to distinguish than two integers with distributions that have little overlap (a large perceived difference). Most numerical cognition research has identified a negatively accelerating perceived difference function (e.g., Campbell, 2005).

Error variance is a critical component of the perceived difference formula. The bounded and unbounded number line tasks reveal different patterns of perceptual errors. The error pattern associated with the bounded number line task was a function of the proportion estimation strategy. We therefore do not consider it an accurate mapping of the psychological representation of integers. In contrast, the error pattern associated with the unbounded number line task was scalar, which is consistent with current theories of integer representation. The scalar variance associated with the error distributions seen in Experiment 2 has important consequences for the perceived difference between integers. The scalar variance (the denominator of Eq. 7) overwhelms the positively accelerating perceived mean distance function (the numerator in Eq. 7), resulting in a negatively accelerating perceived difference function. So, as target number increases, the perceived difference between successive integers decreases. This finding is consistent with both the linear and logarithmic models of integer representation (and most published data on the topic). Figure 4 presents a description of the psychological representation of integers based on our unbounded number line data.

Fig. 4
figure 4

Graph of perceived difference and distance between numbers. The x-axis represents the estimates of target numbers, and the y-axis represents density. Each curve represents the psychological construct of the labeled target number. There are larger perceived distances between the means of larger numbers than between the means of smaller numbers. Nevertheless, the perceived difference between numbers decreases as target number increases, because there is more distributional overlap as target number increases

Full size image

If one accepts that the bounded number line task is a valid measure of proportion estimation and the unbounded task is a valid measure of integer estimation, the relation between the results of these two tasks provides some clues about the cognitive structures underlying our understanding of proportions and integers. The similarity of the perceived mean distance estimates extracted from the bounded and unbounded tasks suggests that our understanding of proportions is predicated on our understanding of integers. The difference in error patterns supports the supposition that, although our understanding of proportions is predicated on our understanding of integers, the psychological construct of proportion is likely different from that of integers (Cohen, 2010). Additional exploration of this issue will be required to further disentangle these two constructs.

In summary, we found that the numerical bias in estimations is best described by an accelerating power function in both the bounded and unbounded number line tasks. This suggests that both tasks tap into similar psychological constructs. However, the proportion estimation strategy used in the bounded number line task produced measures of error variance related to the proportion estimation. In contrast, the unbounded number line task revealed a scalar variance pattern of error, which is consistent with integer estimation. This pattern, together with the accelerating perceived distance function, resulted in the negatively accelerating perceived difference function ubiquitous in the numerical cognition literature. We conclude that the unbounded number line task is a purer measure of the numerical bias of integers than is the bounded number line task.