Task preparation and task inhibition: a comment on Koch, Gade, Schuch, & Philipp (2010)

Abstract

In their recent review article, Koch, Gade, Schuch, & Philipp, (Psychonomic Bulletin & Review, 17, 1–14, 2010) present compelling evidence for the role of inhibition in task switching, as measured by n-2 repetition costs. They promote the view that inhibition targets response-related processes of task performance rather than cue-based preparatory stages. In support of this distinction, they cite the finding in the literature that n-2 repetition costs are not reduced given longer preparation intervals. In this article, we advocate the analysis of whole reaction time distributions for investigating the influence of task preparation on task inhibition. We present such analyses from two of our published experiments that support the view that n-2 repetition costs can be reduced given sufficient preparation. The results suggest that cue-based processes do contribute to inhibition in task switching.

Koch, Gade, Schuch, and Philipp (2010) provided a comprehensive review of the evidence for inhibitory mechanisms in task-switching designs. Inhibition can be inferred from slower reaction times (RTs) returning to a task recently performed (i.e., ABA sequences) than to a task not recently performed (i.e., CBA sequences). These n-2 repetition costs are believed to reflect the persisting inhibition of task A when it is switched away from at n–1.

Although the evidence that n-2 repetition costs reflect inhibition is compelling, the question as to what exactly is inhibited has become more contentious. In their article, Koch et al. (2010) review evidence from their laboratory that suggests inhibition targets response stages of task performance (e.g., response preparation/execution). They also review evidence that suggests inhibition may be more flexible, targeting those aspects of the task structure that generate the greatest inter-trial conflict when a task switches (Houghton, Pritchard, & Grange, 2009); indeed, research has shown that cue-based preparatory stages of task performance can be the target of inhibition (Grange & Houghton, 2009, 2010b; Houghton et al., 2009). Specifically, using a target detection paradigm, Houghton et al. proposed that on the basis of the task cue, a relevant target representation must be activated in working memory (WM), a process they called cue-target translation. When the relevant target switches, a new representation must be activated in WM; in order to reduce conflict, the previously relevant WM representation must become inhibited, leading to n-2 repetition costs. The process of cue-target translation can be aided by more informative cues (called “transparent” cues), such as a shape that provides a sample of the relevant target property (e.g., if the target is an oval with a thick border, a transparent cue would be a rectangle with a thick border, whereas a less transparent cue would be a plain square; see Grange & Houghton, 2010a). As the environment provides the necessary representation to perform the task with transparent cues, less cue-target translation is required in WM. Thus, when a task switches, there is less conflicting information in WM that requires inhibition. In this instance, no n-2 repetition cost is predicted, as no inhibition of WM representations has occurred. Across several studies, reduced n-2 repetition costs with relatively transparent cues compared to relatively less transparent cues have been reported (Grange & Houghton, 2009, 2010b; Houghton et al., 2009).

Inhibition and preparation in task-switching

In their review, Koch et al. (2010, p. 9) highlight that the account of cue-based stages of task performance being the target of inhibition is inconsistent with the reported finding that n-2 repetition costs are not reduced with greater preparation intervals, as measured by the time between the onset of the task cue and the onset of the task stimulus (cue-stimulus interval, CSI). Koch et al. are correct in their assertion that the hypothesis of Houghton and colleagues would predict such a reduction: given more preparation time, participants should be able to engage in any cue-target translation processes ahead of the stimulus, which would include overcoming residual inhibition of a recently performed task.

In this commentary we argue that an alternative method of investigation—analysing whole reaction time distributions by constructing cumulative distribution frequency (CDF) plots—may provide novel insight as to the influence of preparation on n-2 repetition costs. CDFs are constructed by rank ordering all RTs from fastest to slowest for each individual subject for each condition. Quantiles are calculated for each participant and condition; the quantiles are averaged across participant and plotted. The CDFs provide more detail than average RT alone, as differences between conditions can be examined across the whole RT distribution (from fastest responses to slowest). In task switching, it is assumed that the fastest RTs in the distribution are those in which participants were suitably ready for the upcoming trial (DeJong, 2000), whereas the slowest RTs reflect that proportion of trials in which participants were not prepared. Thus, one can investigate the dynamics of n-2 repetition costs between prepared trials (fast RTs) and unprepared trials (slow RTs): if the n-2 repetition cost can be reduced given greater preparation, such costs should be smaller at the faster end of the RT distribution than at the slower end. This alternative analysis is specifically advantageous because preparation effects can be investigated within one experimental condition—i.e., CSI need not be manipulated.

The current study

CDF construction was employed to investigate the effects of preparation on n-2 repetition costs using data from Grange and Houghton (2010b) where participants were required to search for a relevant oval target on a screen co-present with three other ovals. Each oval differed on a visual property (i.e., one had a thick border, one was shaded in, one was angled, and one was neutral); three of the ovals served as potential targets, whereas the neutral oval was always present as a distractor. The four ovals were positioned with one to each quadrant of the screen. On each trial the participant had to indicate the location of a target oval, as indicated by a preceding cue, by making a spatially compatible finger response (e.g., if the target was in the top left quadrant, the “upper left” finger was used). The target’s location varied randomly on every trial. Crucially, in this paradigm there is no response conflict during a switch as the same response set is maintained throughout, regardless of the identity of the target stimulus.

In Experiment 1 of Grange and Houghton (2010b) arbitrary, non-transparent, cue-target pairings were used, and the pairings used in the first half of the experiment were re-assigned (“re-paired”) in the second half. Thus, three arbitrary cues—an octagon, square, and triangle—were each paired with an oval (e.g., square-shaded oval; triangle-bordered oval; octagon-angled oval). In the second half of the experiment, the same cue and target sets were used, but the pairings were changed (e.g., square-angled oval; triangle-shaded oval; octagon-bordered oval). Cue types in the first half of the experiment are referred to as “standard cues” and the cue type in the second half of the experiment as “switched cues”. In both conditions, the cue was presented centrally for 500 ms followed by a blank screen for 250 ms; after this, the four potential targets appeared, and remained visible until a response was made by the participant. After a response, the screen was blank for an RCI of 500 ms.

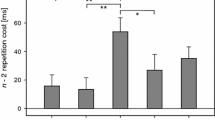
Grange and Houghton (2010b) proposed that the re-assignment of cue-target pairings would increase conflict in WM during cue-target translation. As this should result in increased inhibitory control to reduce this conflict, greater n-2 repetition costs were predicted following the re-assignment. This prediction was confirmed, with an n-2 repetition cost of 20 ms for standard cues and 55 ms for switched cues, indicative of greater inhibition during the second half of the experiment.

Experiment 1 distribution analysis

CDFs were constructed from the data of both conditions in Grange and Houghton (2010b), Experiment 1. The CDFs were constructed from the quantiles 0.05, 0.15, 0.25, 0.35, 0.45, 0.55, 0.65, 0.75, 0.85, and 0.95. Only correct RTs preceded by two correct responses were analysed; RTs slower than 2.5 standard deviations of each participant’s mean were excluded. The trimmed data were analysed in a 2 (cue type: standard vs. switched)  ×  2 (sequence: ABA vs. CBA)  ×  10 (quantile) repeated measures ANOVA. The CDFs of ABA and CBA sequence reaction times for standard and switched cues are shown in Fig. 1a and b.

Fig. 1

Cumulative distribution functions of ABA and CBA sequence reaction times from the standard (a) and the switched cue (b) conditions of Experiment 1 in Grange and Houghton (2010b). N-2 repetition costs are calculated by subtracting CBA RTs from ABA RTs

N-2 repetition costs for both cue types at the fast (prepared) end of the distribution were very small and consistently increased throughout the distribution. For the standard cues, n-2 repetition cost was 6 ms at the 0.05 quantile, consistently increasing to 40 ms at the 0.85 quantile; the n-2 repetition cost reduced to -1 ms at the final quantile. For switched cues, n-2 repetition cost consistently increased from 5 ms at the 0.05 quantile to 123 ms at the 0.95 quantile.

These observations were confirmed in a significant interaction of quantile on sequence [F(9,279) = 6.75, p<.001, η_p ²= .18] due to a significant linear trend [F(1,31) = 16.12, p<.001, η_p ²= .34], confirming the increase in n-2 repetition cost towards the slower end of the distributions.

The three-way interaction was significant [F(9,279) = 5.68, p<.001, η_p ²= .16] due to a difference of the linear trends between cue types [F(1,31) = 11.07, p<.01, η_p ² = .26]. The three-way interaction was investigated by performing separate two-way ANOVAs—one for each cue type—with the factors sequence and quantile. For the standard cues, the quantile by sequence interaction did not reach significance [F(2.44, 75.75)=1.91, p=.15, Greenhouse-Geisser correction]; it reached significance for the switched cues [F(9,279) = 9.67, p<.001, η_p ² = .24] due to a significant linear trend [F(1,31) = 20.28, p<.001, η_p ² = .40].

The lack of an interaction of quantile on sequence for standard cues appeared to be driven by the lack of n-2 repetition cost at the final quantile. Removal of this quantile from the analysis introduced a significant quantile-by-sequence interaction [F(2.68, 83.03) = 3.48, p<.05, η_p ² = .10] due to a significant linear trend [F(1,31) = 7.09, p<.05, η_p ² = .19]. The reason for this reduction of n-2 repetition cost at the final quantile is unclear; it is possible that at the tail end of the distribution measurements become noisier due to increased variance associated with slower responding. For the purposes of the present exposition, we are more interested in the dynamics of n-2 repetition cost at the faster end of the distribution, which were vastly reduced.

Discussion

Distributional analysis of Experiment 1 from Grange and Houghton (2010b) suggests that n-2 repetition costs can be reduced given sufficient preparation time (i.e., at the faster end of the RT distribution). However, the increase in n-2 repetition cost throughout the RT distribution could be due to a peculiarity of slow responding per se, independent of the degree of preparation. To address this, distributional analysis of Experiment 2 from Grange and Houghton (2010b) was performed. This experiment included a condition with non-transparent cue-target pairings (the cues and targets were identical to that in the standard cues from Experiment 1) and one condition where the cue-target pairings were maximally transparent. The maximally transparent condition used the cues from Experiment 1, but now the target display consisted of a square, triangle, and octagon (still with the neutral oval distractor); participants in this condition merely had to find the same shape that was presented as the cue. The matching cues and target condition are referred to as the “related-cue” condition, and the cues and targets used in Experiment 1 as the “unrelated-cue” condition.

In the related-cue condition, little cue-target translation has to be performed in WM as the cue provides the necessary representation directly. Thus Grange and Houghton (2010b) predicted no n-2 repetition cost for this condition. The results revealed a significant 26-ms cost for the unrelated cues and a non-significant cost of 3 ms for the related cues.

Analysis of the RT distributions from this experiment provides additional evidence in support of the current proposal: if the increasing n-2 repetition costs found at the slower ends of the RT distribution from Experiment 1 were due to a peculiarity of slow responses per se, such a pattern should be present even in a condition that produces no n-2 repetition cost in mean RT (i.e., related cues). However, if the pattern found for Experiment 1 was due to a reduction of n-2 repetition cost given greater preparation, no n-2 repetition cost should be evident throughout the entire distribution for the related cues.

This analysis also allows us to compare statistically the interaction of quantile on n-2 repetition cost between a condition that produces an n-2 repetition cost (unrelated cues) and a condition that does not (related cues).

Experiment 2 distribution analysis

The data trimming was identical to that of Experiment 1. The trimmed data for this experiment were analysed in a 2 (cue type: unrelated vs. related)×2 (sequence: ABA vs. CBA)×10 (quantile) repeated measures ANOVA. The CDFs of ABA and CBA sequence reaction times unrelated and related cues are shown in Fig. 2a and b.

Fig. 2

Cumulative distribution functions of ABA and CBA sequence reaction times from the unrelated (a) and the related cue (b) conditions of Experiment 2 in Grange and Houghton (2010a, b)

For the unrelated cues, there was no n-2 repetition cost at the 0.05 quantile (-1.7 ms), but the cost consistently increased up to 59 ms at the 0.85 quantile; similar to the standard cues in the Experiment 1 analysis, the n-2 repetition cost for the unrelated cues was reduced to 16 ms at the final quantile. For the related cues, the n-2 repetition cost was absent throughout the distribution; the maximum value was at the 0.85 quantile (6 ms).

These observations were supported by a significant three-way interaction [F(9,279) = 3.84, p<.05, η_p ² = .11] due to a difference of the linear trends between cue types [F(1,31) = 4.83, p<.05, η_p ²=.14]; the cubic trend was also significant for this interaction [F(1,31) = 7.59, p<.05, η_p ² = .20]

The three-way interaction was investigated by performing separate two-way ANOVAs—one for each cue type—with the factors sequence and quantile. For the unrelated cues, the interaction of quantile on sequence was significant [F(9,279) = 4.38, p<.01, η_p ² = .12] due to a significant linear [F(1,31) = 6.29, p<.05, η_p ² = .17] and cubic trend [F(1,31) = 6.57, p<.05, η_p ² = .18]. The linear trend was driven by an increase in n-2 repetition cost toward the slower end of the distribution; the cubic trend was driven by a reduction of the n-2 repetition cost at the final quantile (see Fig. 2a).

The interaction of quantile on sequence for the related cues was not significant [F(9,279)<1]; n-2 repetition costs were absent throughout the entire distribution.

Discussion

The results from the distributional analysis of Experiment 2 from Grange and Houghton (2010b) were clear: no n-2 repetition cost was apparent throughout the RT distribution for the related cues. Therefore, the increase of the n-2 repetition cost throughout the distribution found in Experiment 1 cannot be due to a peculiarity of slow responding per se. For the unrelated cues, the finding from Experiment 1 was replicated, with no n-2 repetition cost toward the faster end of the RT distribution.

General discussion

By analysing RT distributions from two experiments that produce varied sizes of n-2 repetition costs, novel evidence that inhibition can be overcome given sufficient preparation has been provided. N-2 repetition cost at the faster end of the distribution was consistently smaller than at the slower end; this pattern of results cannot be explained by an effect of general slowing (see the related cues from Experiment 2), and the effect varies with the mean magnitude of the n-2 repetition cost (i.e., the three-way interaction in Experiment 1).

The finding of variation in the n-2 repetition cost across the RT distribution reported here stands against the finding of Schneider and Verbruggen (2008) who reported consistent n-2 repetition costs across the whole distribution in their multiple-mapping condition (triangular data points in their Fig. 1). Unlike the results reported here, the linear trend for the interaction of quantile on sequence was not significant in their study.¹ However, differences between paradigms may explain the discrepant results. For example, their paradigm has considerable inter-trial conflict centred on response processes, raising the possibility that n-2 repetition costs in such paradigms are—despite the arguments presented in this commentary—impervious to cue-based preparation effects (but see Karayanidis, Jamadar, Ruge, Phillips, Heathcote, & Forstmann, 2010). This possibility predicts that CDFs of the data from Koch’s laboratory may also show no effect of preparation, as inter-trial conflict in their studies is consistently centred on response processes. Conversely, any paradigm where conflict is centred on cue processing may produce the same CDF results as reported in this article. Further work comparing RT distributions between different paradigms will be an important step forward in addressing this issue.

Are faster RTs due to preparation?

Not all authors agree with the assertion that fast responses are indicative of full task preparation. Originally, DeJong (2000) argued that participants fail to prepare for a task on some trials leading to slower RTs; however, when they responded quickly, their preparation was full. In contrast, Lien, Ruthruff, Remington, and Johnston (2005) argued that task preparation always occurs, but is only partial, or as they put it, participants prepare some of the task all of the time, rather than all of the task some of the time.

In particular, Lien et al. (2005) suggest that this partial preparation involves the activation of a component of the stimulus response (SR) mapping. For example, if the task on a given trial is to judge whether a presented shape is red or green, and the SR mapping is a left key press for “Red” and a right key press for “Green”, participants can prepare for the left key press “Red” when presented with the cue for the colour task. On those proportion of trials in which the stimulus is indeed red, the participants response will be speeded compared to when the stimulus is actually green. This partial preparation thus pays off on a proportion of trials leading to faster responding when the stimulus is congruent with the partially prepared response.

By this notion, the RT differences reported here could reflect partial—but consistent—preparation of a component of the task. The present data can neither support nor refute this idea, but we would argue that such “pre-emptive guessing” is unlikely to be employed in these studies. In the target-detection paradigm (employed here), participants cannot prepare a partial SR mapping, as the mappings are not fixed (target location is random). Furthermore, when four responses are used (as opposed to two), preparing to make one of the possible responses is counterproductive, as on most trials the wrong response will be selected. However, even if the present results were to reflect such strategies, this does not contradict the idea that preparation can affect n-2 repetition costs. Rather, it supports the view that some aspect of the preparatory process affects these costs, an effect not anticipated by extant null interactions of CSI with task sequence. Even if participants prepare some of the task all of the time, when the partial preparation is congruent with the correct response, no n-2 repetition costs are evident, thus suggesting preparation can overcome inhibition.

All that can be prepared during the CSI in the paradigm of Grange and Houghton (2010b) is a WM representation of the relevant target (i.e., cue-target translation). Therefore, trial-to-trial variation in the speed of this formation might account for the data reported. What drives this variation in WM representation formation is an open question for future investigation. An alternative possibility is that RT variability—and with it variation in the n-2 repetition cost— is affected by a participant’s alertness on a given trial, which could explain the variability without resorting to notions of task-specific preparation. Indeed, manipulation of phasic alertness has been shown to reduce residual switch costs in task switching designs (Meiran & Chorev, 2005). To aid these future investigations, the backward inhibition literature would benefit from an explicit computational model of all processing stages. Such a model would help formalise the growing number of effects of inhibition in task switching reviewed by Koch et al. (2010).

Other possible explanations of the present results are that n-2 repetition costs are absent at the faster end of the RT distribution as these responses may reflect fast guesses or may be due to response repetitions.² Regarding response repetitions (which in the present paradigm are defined by identical stimulus location from trial n-1 to n), it should be noted that the pattern of results for Experiment 1 was qualitatively identical with response repetitions removed: for standard cues, n-2 repetition cost increased from 4 ms at the .05 quantile to 69 ms at the .85 quantile, then reduced to 41 ms at the final quantile. For the switched cues, n-2 repetition cost was 7 ms at the first quantile and consistently increased to 109 ms at the final quantile.

Regarding fast guesses, this idea is undermined by two observations: first, with four possible responses, a guessing strategy would lead to relatively large error rates; however, error rates for Experiments 1 and 2 of Grange and Houghton (2010b) were low (see Table 1). Secondly, mean error RTs are consistently slower than correct RTs (Table 1); if the lack of an n-2 repetition cost at the faster end of the RT distribution were due to fast guesses, one would anticipate faster error RTs than correct RTs; this is clearly not the case.

Table 1 Error rates (%) and mean (M) reaction time in milliseconds (ms) for error and correct responses across n-2 repetitions and n-2 switches for two experiments from Grange & Houghton (2010b). Standard errors are in parentheses

Conclusion

Koch et al. (2010) argue that the absence of an effect of CSI on n-2 repetition costs provides evidence against the proposal that inhibition can target cue-based preparatory stages of task performance (Houghton et al., 2009). In this article, we argue that analysis of RT distributions provides a novel insight into the effects of preparation on inhibition in task switching and supports the view that inhibition can target cue-based preparatory processes. It is hoped in addition that this commentary will help stimulate future studies to go beyond the analysis of mean RTs in the investigation of the mechanisms of task switching.