To quit or not to quit in dynamic search

Abstract

Searching for targets among similar distractors requires more time as the number of items increases, with search efficiency measured by the slope of the reaction-time (RT)/set-size function. Horowitz and Wolfe (Nature, 394(6693), 575–577, 1998) found that the target-present RT slopes were as similar for “dynamic” as for standard static search, even though the items were randomly reshuffled every 110 ms in dynamic search. Somewhat surprisingly, attempts to understand dynamic search have ignored that the target-absent RT slope was as low (or “flat”) as the target-present slope—so that the mechanisms driving search performance under dynamic conditions remain unclear. Here, we report three experiments that further explored search in dynamic versus static displays. Experiment 1 confirmed that the target-absent:target-present slope ratio was close to or smaller than 1 in dynamic search, as compared with being close to or above 2 in static search. This pattern did not change when reward was assigned to either correct target-absent or correct target-present responses (Experiment 2), or when the search difficulty was increased (Experiment 3). Combining analysis of search sensitivity and response criteria, we developed a multiple-decisions model that successfully accounts for the differential slope patterns in dynamic versus static search. Two factors in the model turned out to be critical for generating the 1:1 slope ratio in dynamic search: the “quit-the-search” decision variable accumulated based upon the likelihood of “target absence” within each individual sample in the multiple-decisions process, whilst the stopping threshold was a linear function of the set size and reward manipulation.

Significance

When to quit plays a critical role in visual search. Here we investigated search performance under dynamic and static search, and developed a multiple-decision model with a quitting strategy that successfully accounts for the 1:1 search slope ratios for target-absent and target-present trials in dynamic search, for which classic search models fail to provide a ready account.

The challenge of dynamic search

Anne Treisman’s feature integration theory (FIT; Treisman, 1986; Treisman & Gelade, 1980) is one of the early influential search models to draw a distinction between parallel and serial search. According to FIT, memory plays a critical role in serial search when a target is defined by a conjunction of features (such as when looking for a T amongst Ls). In this case, items are selected and processed serially by focal attention, with rechecking of already attended items prevented by some “inhibition of return (IOR)”-type tagging mechanism (Klein, 1988), yielding a linearly increasing function relating search time to the total number of items in the display (the set size). Assuming effective memory (i.e., item selection without replacement), FIT predicts the search slope for target-absent trials to be about double the slope for target-present trials (Treisman & Gelade, 1980) because, on average, only about half the items would need to be inspected to make a target-present decision, whereas all items need to be scanned (exhaustively) to make a target-absent decision.

Since Treisman’s initial proposal, a substantial body of research has investigated the mechanisms that determine search performance in static displays (for a review, see Hulleman & Olivers, 2015; Kristjánsson, 2015; Wolfe & Horowitz, 2017). Much less work has been devoted to search scenarios in which all display items are in motion—despite the fact that, in everyday life, we often look for a moving target amongst multiple other moving distractors, such as when trying to find a friend in a central railway station where there is a constant stream of people coming and going. Unlike static search, in which scanned items can be tagged for IOR, search of moving items is relatively hard, though still doable. In a recent study, Young and Hulleman (2013) investigated whether search (eye-movement) behavior would differ between static displays and displays with continuous random movement of the items. They found little difference between these two types of search; in fact, in both cases, search was mediated only by the “functional visual field” (FVF) within an eye fixation, the size of which depends on the difficulty of the target–distractor discrimination inherent in the task. Interestingly, in their study, the search slope was still twice as steep for target-absent trials as for target-present trials with randomly, but continuously moving items, suggesting that IOR-based search guidance – in Young and Hulleman’s (2013) terms, “the avoidance of parts of the display to which eye movements have already been made” (p. 186)—was similarly effective in both types of search.

To challenge the role of memory in search even further, Horowitz and Wolfe (1998, 2003) pushed dynamic visual search to the extreme: They designed a search display in which all search items were abruptly (rather than continuously) reshuffled to unpredictable locations every 110 ms, rendering even dynamic inhibitory tracking (Müller & von Mühlenen, 1996) of individual items and exhaustive search virtually impossible. Yet observers were still able to perform the task reasonably well, with relatively low error rates. Surprisingly, although search RTs were overall slower for dynamic as compared with static search, for target-present trials, the slope of the RT/set-size function was nearly the same with dynamic as with the static search displays. In a follow-up study (Horowitz & Wolfe, 2003), the target-present slopes remained similar for static and dynamic search displays when the set size was increased (from the original 16 to 60 items) and the reshuffling rate was decreased (from the original 9 to 2 Hz), or the target was constrained to be positioned or moving within a specific display region. These findings led Horowitz and Wolfe (1998, 2003) to reject the notion of serial search being aided by an IOR-type tagging mechanism. Instead, they advocated an “amnesic search” model according to which memory for already scanned locations or items plays little, if any, role in the guidance of serial search.

This proposal provided strong challenge to a core assumption of many search models (namely, of near-perfect memory for the guidance of serial search) and immediately instigated a vigorous debate (Kristjánsson, 2000; Müller & von Mühlenen, 2000; Peterson, Kramer, Wang, Irwin, & McCarley, 2001; Shore & Klein, 2000; von Mühlenen, Müller, & Müller, 2003). This upshot of this debate was that, although memory cannot have played a role in Horowitz and Wolfe’s (1998) dynamic search scenario, one cannot conclude from this that memory plays no role in standard static and moving scenarios. Concerning the latter, even Young and Hulleman (2013) concluded that “the number of fixations that can be used to avoid revisits . . . is probably smaller than 6” (p. 186), consistent with McCarley, Wang, Kramer, Irwin, and Peterson’s (2003) estimate of 3–4 fixations.

One issue, however, that was ignored in this debate is why the search slope ratios were not the same in Horowitz and Wolfe’s dynamic search condition relative to their static condition, even though the response times (RTs) were generally slower in dynamic search (Horowitz & Wolfe, 1998, 2003; Shore & Klein, 2000)—and, more generally, what we might learn from this extreme situation (as with other extreme scenarios, such as search under conditions of very low target prevalence; e.g., Wolfe, Horowitz, & Kenner, 2005) with respect to the decision mechanisms that govern search RT performance. Of note in this regard, to support their proposal of amnesic search, Horowitz and Wolfe (1998) relied on the target-present slopes because “their interpretation is more straightforward” (p. 575), and the subsequent debate followed suit. Strikingly, however, the target-absent versus target-present slope ratio was close to 1:1 for dynamic search (see Table 1 in Horowitz & Wolfe, 1998; Fig. 2 in Shore & Klein, 2000), which is substantially lower than the 2:1 ratio associated with standard serial search (Treisman & Gelade, 1980; Van Zandt & Townsend, 1993). As mentioned above, a target-absent:target-present slope ratio of 2:1 or above is the hallmark of memory-guided serial search: on target-present trials, search self-terminates as soon as the target is found, statistically after having scanned about half the display items; on target-absent trials, by contrast, all items need to be scanned exhaustively, (ideally) without revisiting any already inspected items, to establish target absence. On this standard model, the 1:1 search slope ratio repeatedly observed in Horowitz and Wolfe’s dynamic search condition is clearly “exceptional.” It should be stressed that search performance is generally slower in dynamic as compared with static search, but as such this fails to explain why the search slope for target-absent trials would be flatter in dynamic search. This raises the fundamental question of how target-absent and target-present decisions are actually made in dynamic search.

When to quit (dynamic) search?

We argue that the key to answering this question is understanding the process of search termination, and for this the challenge mainly comes from target-absent conditions—in Wolfe’s (2012) words, “what is the signal that allows you to quit if no target is found?” (p. 184). Similar to many everyday-life search tasks that do not involve a predetermined “set size” of items, or locations, to be inspected to find some target or a fixed number of targets, such as in foraging, exhaustive search would not be an optimal choice in the face of the constantly relocating search items in dynamic search. In fact, there are scenarios, including the dynamic target-absent condition, in which exhaustive search would even be impossible. In such situations, search must quit without scanning through all items or locations, as otherwise there may be a (potentially infinite) cost in terms of search time. For instance, in a foraging task, Wolfe (2013) found observers tended not to search exhaustively even when explicitly asked to stop searching only when all targets had been found. Looking for a target in Horowitz and Wolfe’s (artificial) dynamic search displays in some way resembles real-life foraging tasks or quality control on a production line, where the products to be inspected for a fault are presented to the human operator at either an externally determined (constant) or a self-paced rate. Regarding the latter task, the similarity is that each successively presented product/item can contain a to-be-detected fault (the item has to be removed from the production line upon detecting a fault) and the operator may know that statistically a certain percentage of products is faulty within a batch. In such scenarios, the “observer” repeatedly encounters a decision point: “Should I quit routine examination and move on to the next patch/item, or should I engage in an in-depth inspection?” or “Should I stop examining a given batch and move on to the next one?” Thus, understanding decision behavior in dynamic search can help us better understand quitting processes in real dynamic environments more generally.

Surveying multiple candidate models for the quitting process, Wolfe (2012) suggested that timing or counting models would be amongst the most promising candidates—that is, observers may use information of the mean search time based on prior history to set a quitting threshold; or, equivalently, they quit after sampling some threshold number of items. Of note, setting a threshold for quitting determines the overall speed–accuracy trade-off. To keep the response times and error rates at the desired levels, observers need to take into account a variety of factors, including the difficulty of the search, set size, target prevalence, and history of response errors (Chun & Wolfe, 1996; Wolfe et al., 2005). For instance, RTs have been shown to become faster on target-absent trials while target-miss rates greatly increased when target prevalence reduced from 50% to 1% (Wolfe et al., 2005). This pattern was driven by a lowering of the quitting threshold (i.e., faster “no” responses) to speed up the average search time while maintaining the overall error rates (including both miss and false alarm) at a certain level. Concerning the search scenarios at issue here, the error rates were generally higher in the dynamic, compared with the static, condition, indicative of a possible speed–accuracy trade-off. To rule out potential confounding, Horowitz and Wolfe (2013) examined median RTs and inverse-efficiency (RT/accuracy) scores in further analyses, with much the same results. However, which quitting process is actually adopted for dynamic search remains unknown to date.

A quitting process has been introduced in recent, multistage search models (Moran, Zehetleitner, Müller, & Usher, 2013; Wolfe, 2012; Wolfe & Van Wert, 2010), which assume that search involves multiple loops of focal-attentional item selection and (“target yes/no”) decision processes, with the exit from the loop controlled by a search termination process. Wolfe and Van Wert (2010) proposed that the quitting is driven by a diffusion process, with the quitting threshold being a linear function of target prevalence. Moran et al. (2013) assumed that the activation (of a unit) for quitting is relative to the “overall activation” on the search-guiding saliency map, with the quitting activation increasing linearly after each distractor rejection. Both models thus implement some kind of “urge to quit” over the time. An alternative to time-based quitting would be to terminate search after having processed a certain proportion of items (Chun & Wolfe, 1996). This has been implemented in the context of the guided search model (Wolfe, 1994; Wolfe & Gray, 2007): Attention is deployed from item to item in the order of decreasing activation strength, which is essentially a function of the likelihood of an item being a target. On target-absent trials, high (“noisy”) activation distractors will be rejected serially. Search is terminated when the activation of the remaining items is below a certain activation level. However, given that both time-based and activation-based models only consider static search scenarios, they both are silent about what would make any difference between Horowitz and Wolfe’s (1998) static and dynamic search conditions. In particular, they have no explanatory value as to the flat, 1:1, search slope ratio in dynamic search, leaving open the question of what factors drive this ratio in this scenario. In particular, would task difficulty alter the quitting process and so, in turn, affect the search slope ratio? And would the search slope ratio change when reward is applied asymmetrically to target-present and target-absent decisions? It has been shown that observers can optimize the accrued total reward by biasing their decision choice towards high-reward targets when the search array contains various possible targets with varying associated rewards (Eckstein, Schoonveld, & Zhang, 2010; Navalpakkam, Koch, Rangel, & Perona, 2010). Reward changes saccadic behavior, too—saccades are made more frequent towards high-reward as compared with low-reward targets (Navalpakkam et al., 2010), and saccade latencies are shorter towards locations associated with higher reward (Sohn & Lee, 2006). Note, however, that all those studies exclusively used static search conditions. So, to date, there is no work that has examined the relations between reward (as a factor potentially influencing quitting decisions) and search slope ratios in dynamic search.

The key characteristic of dynamic search is search with replacement, which resets the sampling probability of the target during the loop of item selection, like Zeus resetting the rolling rock for Sisyphus. Unlike Sisyphus, however, human observers are able to accumulate information across multiple selections (or fixations) to decide when to quit. If we assume that, in each selection (fixation), d items are selected from n items, the probability of the target not being selected for any unit time in dynamic search is given by (1 − d/n). Thus, the probability that the target has still not been selected after t steps is (1 − d/n)^t, which decreases exponentially over time t. This is useful information for gauging when to quit. The rate of decrease becomes slower as the set size n increases. For target-present trials, (1 − d/n)^t is the miss rate when observers quit after t times of selection and rejection. Thus, if an ideal, stubborn observer wished to keep the miss rate equal across the different set sizes, the time to quit would have to be doubled when the set size is doubled¹ (see also Horowitz, 2005, for theoretical analysis). Studies on dynamic search (e.g., Geyer, Von Mühlenen, & Müller, 2007; Horowitz & Wolfe, 1998; von Mühlenen et al., 2003), however, revealed RTs to increase only mildly with a doubling of the set size. This indicates that real observers leverage a trade-off between waiting to accumulate more information and the rate of error production (Shi & Elliott, 2005). A trade-off of this sort may play a critical role in determining RTs and search slopes (Fleck & Mitroff, 2007), although the underlying mechanism remains unclear.

On this background, we aimed to investigate how the quitting process influences the even 1:1 search slope ratio for target-absent and target-present trials in dynamic search, as well as the standard 2:1 ratio in static search. In addition, we developed a computational model, deriving from “conventional” assumptions about serial search, which can provide a coherent account of the complete pattern of behavioral indices (from target-absent as well as target-present trials) of how dynamic search is performed. Given that the quitting process directly influences the decision thresholds for target-present and target-absent responses, we systematically manipulated the response payoffs and task difficulty to influence the target-miss and the false-alarm rates, and we used signal-detection theory (SDT; Swets & Green, 1965) to analyze the trade-off function and determine the main factors that contribute to the quitting process. This was done in three experiments. Experiment 1 was designed to replicate Horowitz and Wolfe’s (1998) original study and compare the target-absent versus target-present search slope ratios between dynamic and static search. In Experiment 2, monetary reward was introduced to manipulate the response criteria, to examine how the quitting time would affect the search slopes. This involved two sessions: in one session, participants were rewarded for correctly discerning “target presence” and in the other for correctly establishing “target absence.” We hypothesized that reward payoffs would change response criteria, thus altering the quitting process. If the payoffs influence only the general “readiness to respond,” this would merely predict an additive shift in the RT levels, without altering the search slope ratios. In contrast, observing a change in the RT slopes would indicate that the payoffs have a differential effect (on the quitting process) across the set sizes. In standard static search, increasing search difficulty typically steepens the search slopes, but the slope ratio remains the same as that primarily determined by the serial search strategy. Yet it is not clear whether search difficulty would have similar effects in dynamic search. Thus, in Experiment 3, search difficulty was varied to manipulate decision sensitivity and examine whether task difficulty would influence the quitting process, thus determining the search slopes and overall RTs. In the modeling section, we integrated the multiple-decisions model (Wolfe & Van Wert, 2010) with SDT analysis to model the quitting process, thus expanding the multiple-decisions model to dynamic search.

Method

Participants

Thirty-five university students, recruited from Ludwig-Maximilians-Universität Munich, took part in three experiments (11 in Experiment 1 and 12 each in Experiments 2 and 3; 25 females; mean age = 26.2 years). All had normal or corrected-to-normal visual acuity. Sample size was determined based on previous studies (Geyer et al., 2007; Horowitz & Wolfe, 1998) and a classic search paradigm (search for a T amongst Ls), which usually yields a search slope of some 20 ms/item on target-present trials, and RT difference between target-present and target-absent trials is larger than the standard deviation of the mean RTs (i.e., effect size d > 1). Thus, based on a standard Cohen’s d = 1 and power of 0.85, the sample is 11. All participants gave written informed consent prior to the experiment and were paid €8 per hour for their participation. In Experiment 2, participants earned additional monetary reward (up to €4.20 maximally). The study was approved by the Ethics Board of the LMU Faculty of Pedagogics and Psychology.

Stimuli and apparatus

The experiments were carried out in a sound-reduced and moderately lit experimental cabin. Stimuli were generated by Psychophysics Toolbox (Version 3; Kleiner, Brainard, & Pelli, 2007) based upon MATLAB (The MathWorks, Inc). They were presented on a 21-inch LACIE CRT monitor with a screen resolution of 1,024×768 pixels and a refresh rate of 100 Hz.

The search displays (see Fig. 1 for an example display) were composed of a set of letters. Target-present displays consisted of one T target item and multiple distractor Ls (varying from 7–11 to 15 items); target-absent displays consisted of distractor Ls only (eight, 12, or 16 items). Each letter subtended 0.67 °  × 0.67°of visual angle and was randomly rotated in one of four orthogonal orientations (0 ° , 90 ° , 180 ° ,or 270°). In Experiment 3, the vertical line of the letters L was shifted 0.095°inward, increasing their similarity to the target T and thus making the search task more difficult compared with Experiments 1 and 2. In Experiments 1 and 2, all search items were randomly arranged within the central screen region subtending 14 °  × 14°. In Experiment 3, the density of the search items was kept constant (on average, 1.3 items per 1 °  × 1° area) across three different set sizes (eight, 12, and 16 items), and the maximum display region was 12 °  × 12°. To balance the possible regions within which the search display would occur in Experiment 3, the center of the small set-size display varied across trials, such that the possible item locations across the different set sizes remained the same.

Fig. 1

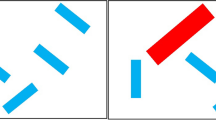
An example static display in which a T target is present (in the upper left quadrant). Stimuli were randomly rotated T (target) and L (distractor) items. In the static search condition, the search items remained at the same locations until a response was made. In the dynamic condition, the positions of the items were randomly shuffled every 110 ms

Procedure

Participants viewed the display from a distance of 60 cm, maintained with the support of a chin rest. A trial started with presentation of a fixation cross in the center of the display for 500 ms, followed by the search display. The number of search items was randomly selected from eight, 12, or 16. There were two types of search: static and dynamic. In static search, the search items remained at the same, fixed locations within the search display until the participant issued a (target-present/target-absent) response or for a maximum of 5 seconds without a response. In dynamic search, the positions of the search items were randomly regenerated every 110 ms; that is, search items changed their positions every 110 ms. Again, this continued until participant’s response or for 5 seconds maximum, at which time the trial terminated. Static and dynamic search displays were presented in separate trial blocks. There were seven blocks per (static, dynamic) search condition, and were presented randomly interleaved. Participants were instructed to discern the presence versus absence of a target T in the search display as rapidly and accurately as possible, by pressing the left (yes) or right (no) arrow key on the keyboard with their left or right index finger, respectively. In addition, they were informed that target-present and target-absent trials were equally likely. The next trial started after a random intertrial interval of 1.0 to 1.2 seconds with a blank screen. Prior to performing the search task, participants performed two unrecorded trial blocks (one for the static and one for the dynamic condition) to become familiar with the search displays. Participants were free to take a break between blocks.

Design

Experiment 1 consisted of 14 trial blocks (seven static and seven dynamic, 14 blocks randomly interleaved), each block with 30 (i.e., 15 target-present and 15 target-absent) trials. The order of blocks were randomized. Thus, a total of 420 trials were presented during the whole experiment.

Experiment 2 consisted of two sessions, each comprising 420 trials with the same stimulus configurations as in Experiment 1. In addition, participants were provided with reward feedback—the message “Correct! You earned 1 more cent”—after a certain type of correct response. In one session, they received the reward (feedback) whenever they correctly responded “target present”; in the other session, whenever they correctly responded “target absent.” Incorrect responses or correct responses to the opposite condition within were not rewarded, and no feedback was provided. At the end of each trial block, participants received information about how much they had earned additionally. The total additional earnings were then paid on top of the basic remuneration. The two reward conditions were administered counterbalanced across participants.

Experiment 3 was essentially the same as Experiment 1, except that the vertical line of the distractor L was shifted inward by a small amount, making it more similar to the target T, thus increasing the difficulty of the search task. In addition, an auditory, 300-Hz warning signal was sounded for 500 ms when participants made an error. And the total number of trials was increased to 576.

Results and discussion

All correct RTs reported below exclude outliers, defined as trials on which RTs were outside of 2.5 sigma (about 1.2% of trials) or faster than 100 ms (“anticipations”), as well as trials on which participants made an incorrect response. For the analysis of response sensitivity and bias, target presence and absence were regarded as signal and noise, respectively. The sensitivity parameter d′ and the response bias C were calculated from the hit rate (i.e., rate of correct target-present responses) and the false-alarm rate (i.e., rate of incorrect target-present responses), following standard SDT (Wickens, 2002). Some observers made perfect responses in some easy conditions (e.g., in small set-size static search). For such extreme values (i.e., hit rates of 1 and false-alarm rates of 0), we made adjustments according to a commonly applied remedy (Macmillan & Kaplan, 1985; Stanislaw & Todorov, 1999): rates of 0 were replaced by 0.5/n, and rates of 1 by 1 − 0.5/n, where n is the number of target-absent and target-present trials, respectively. All statistical tests were conducted using repeated-measures ANOVAs, with additional Bayes factor analyses to comply with the more stringent criteria required for acceptance of the null hypothesis (Kass & Raftery, 1995; Rouder, Speckman, Sun, Morey, & Iverson, 2009).

Experiment 1

Figure 2 presents the mean correct RTs, along with the error rates, as a function of set size, separately for target-present and target-absent trials, and for the dynamic and static search conditions. RTs were examined using a repeated-measures ANOVA with three factors target (present, absent), search type (static, dynamic), and set size (eight, 12, 16). Consistent with previous findings (Horowitz & Wolfe, 1998; von Mühlenen et al., 2003), mean RTs were slower in the dynamic search (1,780 ms) compared with the static search (1,180 ms) condition, F(1, 10) = 15.25, p = .003, η_g = .23, and slower on target-absent (1,880 ms) compared with target-present trials (1,080 ms), F(1, 10) = 38.1, p < .001, η_g = .35. Moreover, RTs increased as set size increased, F(2, 20) = 44.7, p < .001, η_g = .05. In addition, all two-way and three-way interactions were significant (all ps < .031). The significantly slower RTs in dynamic search were likely caused by the abrupt reset of the search display every 110 ms. This may lead to extended “dwelling” at a given fixation location (Geyer et al., 2007; von Mühlenen et al., 2003). Also, selection time for each sampled patch (including one or more items) may vary and be out of sync with the 110-ms updating cycle. Thus, the random reshuffling of the search items every 110 ms would disturb/reset ongoing item selection processes, generally slowing information accumulation in dynamic search, to which observers would react by setting the quitting threshold relatively high. We will return to the issue of the quitting threshold in the Modeling section.

Fig. 2

Results for Experiment 1. Mean correct RTs (lines, upper panels) and mean error rates (bars, lower panels), with associated standard errors, as a function of set size, separately for target-present and target-absent trials. The left panels present the results for dynamic search; the right panels for static search. (Color figure online)

To understand the interactions, we further examined the search slopes, response sensitivities, and biases. The slopes were estimated from RT×set size function for each of the four two-factor combinations (target ×search type). Sensitivities and biases were estimated from the target-present and target-absent trials for each of the six two-factor combinations (set size×search type). Figure 3a presents the mean search slopes as a function of search type and target. A repeated-measures ANOVA revealed both main effects, target, F(1, 10) = 14.6, p = .003, η_g = .2; search type, F(1, 10) = 6.3, p = .03, η_g = .11, as well as the interaction to be significant, F(1, 10) = 16.27, p = .0023, η_g = .21. The interaction was mainly caused by the steep slope in the static target-absent condition. The ratio of the “absent” (73 ms/item) to the “present” (21.8 ms/item) slopes in static search exceeded 3. The “present” slopes were not significantly different between the dynamic and static search conditions, (29.5 vs. 21.8 ms/item), F(1, 10) = 0.9, p = .36, η_g = .037, BF = 0.56, replicating the previous studies (Geyer et al., 2007; Horowitz & Wolfe, 1998). Importantly, unlike the static display, the slope of the dynamic target-absent condition (28.7 ms/item) did not differ from that in the dynamic target-present condition (29.5 ms/item), F(1, 10) = 0.013, p = .91, BF=.39, which had been ignored previously. The differential slopes for the “absent” trials between the static and dynamic search conditions strongly suggest that participants applied different termination strategies in the two types of search. Based on eye-tracking evidence, previous studies (Geyer et al., 2007; von Mühlenen et al., 2003) have suggested that the two conditions induce qualitatively different search strategies (e.g., “sit-and-wait” for dynamic search), which affects mean RTs in general, resulting in overall slower responses for dynamic compared with static search (see Fig. 1). However, merely assuming a sit-and-wait strategy would not explain the differential slope ratios between dynamic and static search: Extended fixational dwelling on a limited number of (attentionally sampled) patches alone would only cause a delay in responding but would not tell the observer anything about when to quit search. Thus, it remains unclear from the eye-movement studies whether the two types of search involve similar or different processes of search termination.² Thus, it remains unclear from these studies whether the two types of search involve similar or different processes of search termination.

Fig. 3

a Mean search slopes (ms/item), with associated standard errors, in Experiment 1. b Target discrimination sensitivity d′, with associated standard errors, as a function of display size, separately for dynamic and static search. c Response criterion C, with associated standard error, as a function of display size, separately for dynamic and static search. (Color figure online)

To identify potential different termination processes and speed–accuracy trade-offs, we calculated target-present/target-absent discrimination sensitivity d′ and response bias C (see Fig. 3b–c). In general, finding a T amongst Ls is not that difficult: d′ was higher than 2.5 across all conditions. However, d′ was significantly lower in dynamic than in static search, F(1, 10) = 14.17, p = .004, η_g = .33, likely because search was terminated without having accumulated sufficient information in the dynamic condition: Terminating search with only partial information would yield increased error rates. Furthermore, d′ decreased significantly as set size increased, F(2, 20) = 7.13, p = .005, η_g = .07, indicating that participants became more ready to make a decision with uncertainty (i.e., ready to accept errors) when set size was larger. However, there was no interaction between search type and set size, F(2, 20) = 1.89, p = .17, η_g = .01, BF=0.30. The search slopes in the dynamic search were likely determined by terminating search earlier with high uncertainty (see Discussion for further consideration).

A further repeated-measures ANOVA on the response criteria C revealed a significant effect of search type, F(1, 10) = 14.9, p = .003, η_g = .2. Responses were generally relatively liberal (i.e., participants tended to respond “target present”) in dynamic search (as indicated by the negative C values); by contrast, they were significantly more conservative in static search (i.e., the tendency to respond “target present” significantly increased the false-alarm rates; see Fig. 3). There were no significant effects involving set size, main effect, F(2, 20) = 0.22, p = .80, η_g = .003, BF=0.14; Set Size ×Search Type interaction, F(2, 20) = 0.26, p = .77, η_g = 0.004, BF=0.24].

In summary, Experiment 1 replicated previous findings in showing that “target-present” RT slopes did not differ between static and dynamic searches, while the ratio of target-absent to target-present slopes exceeded 2 in static search. Importantly, there was no slope difference between target-absent and target-present trials in dynamic search. Response preference analysis showed that the shallow target-absent RT slope for dynamic search was likely due to terminating search earlier with high uncertainty (i.e., low response sensitivity) in this search condition.

Experiment 2

In Experiment 2, participants received reward for correct responses on either target-present or target-absent trials, in separate sessions. Figure 4 presents the mean correct RTs, along with the error rates, as a function of set size, separately for the target-present and target-absent trials, and for the dynamic and static search conditions. Inspection of Fig. 4 suggests that reward assigned to correct target-present decisions expedited mean RTs on target-present trials, while slowing responses on target-absent trials. By contrast, reward assigned to correct target-absent decisions sped up responses on target-absent trials but slowed RTs on target-present trials. A repeated-measures ANOVA with factors set size, target, search type, and reward revealed significant main effects of set size, F(2, 22) = 95.3, p < .001, η_g = .06, target, F(1, 11) = 53.9, p < .001, η_g = .43, and search type, F(1, 11) = 15.5, p = .002, η_g = .14, which corroborates the findings of Experiment 1. Interestingly, though, the main effect of reward was nonsignificant, F(1, 11) = 2.55, p = .14, η_g = .005, BF = 0.97. As can be seen from Fig. 5, this came about by participants trading the speed of one type of response against that of the other to gain reward (significant Target × Reward interaction, F(1, 11) = 27.9, p < .001,η_g = .08). Specifically, RTs on target-present trials became faster and miss rates decreased when correct target-present decisions were rewarded; conversely, RTs on target-absent trials became faster and false-alarm rates decreased when correct target-absent decisions were rewarded. On nonreward trials, by contrast, RTs and error rates were shifted in the opposite direction. These patterns suggest that when reward was assigned to the target-present trials, observers lowered their criteria for a target-present decision while increasing the (quitting) threshold for a target-absent decision in order to avoid missing the reward. The opposite strategy was adopted when reward was assigned to the target-absent trials. These findings are consistent with previous studies of static search under reward conditions (Eckstein et al., 2010; Navalpakkam et al., 2010; Sohn & Lee, 2006). Further, besides the Target × Reward interaction, the interactions Set Size × Target, Set Size × Search type, Set Size × Reward, and Set Size × Target × Search Type, Target × Display Type × Reward were all significant (all ps < 0.01). The mean RTs in both reward conditions show similar patterns to those in Experiment 1. To reduce the complexity of the analysis, we went on to focus on the search slopes and response sensitivities and biases (though we come back to the overall mean RTs and error rates in the Modeling section below).

Fig. 4

Results for Experiment 2. Mean correct RTs (lines) and mean error rates (bars), with associated standard errors, as a function of display size, separately for target-present (sold lines) and target-absent trials (dashed lines), and for the reward “absent” (circle symbols) and reward “present” sessions (square symbols). The left panels present the results for dynamic search, the right panels for static search. “RA” denotes reward for correct target-absent responses, and “RP” reward for correct target-present responses. (Color figure online)

Fig. 5

a Mean search slopes (ms/item) with associated standard errors in Experiment 2. b Target discrimination sensitivity d′, with associated standard errors, as a function of set size, separately for the dynamic and static search displays. c The response criterion C, with associated standard errors, as a function of set size, separately for the dynamic and static search conditions. “RA” denotes reward for correct target-absent responses, and “RP” reward for correct target-present responses. (Color figure online)

Search slopes are depicted in Fig. 5a as a function of search type and target. A repeated-measures ANOVA with factors search type, target, and reward revealed the main effects of search type, F(1, 11) = 24.3, p < .001, η_g = .26, and target presence, F(1, 11) = 10.45, p = .008, η_g = .13, to be significant. Slopes were steeper for static versus dynamic search, and for target-absent versus target-present trials. The Target × Search Type interaction also was significant, F(1, 11) = 47.5, p < .001, η_g = .39, owing to steep slopes in the static “absent” condition. Interestingly, the main effect of reward was significant, F(1, 11) = 9.23, p = .011, η_g = .127, but none of the interactions involving reward (all ps > 0.1). Reward associated with target-absent, compared with target-present, trials made the slopes shallower, indicative of a tendency to terminate search earlier with larger set sizes when reward was associated with correct “absent” responses rather than correct “present” responses. Further analysis of the slopes for dynamic search revealed a significant main effect of reward, F(1, 11) = 8.67, p = .013, η_g = .187, with shallower slopes in the “absent” as compared with the “present” reward condition. That is, the target-absent:target-present slope ratio was smaller than 1. Consistent with Experiment 1, the slope difference between target-present and target-absent trials failed to reach significance, F(1, 11) = 3.94, p = .072, η_g = .13, BF=6.0.

An ANOVA on d′ revealed the main effects of search type, F(1, 11) = 87.3, p < .001, η_g = 0.45, and set size, F(2, 22) = 13.05, p < .001, η_g = .08, to be significant, but not that of reward, F(1, 11) = 2.27, p = .16, η_g = .02, suggesting that search sensitivity was unaffected by reward. Similar to Experiment 1, on average, target-present/target-absent discrimination sensitivity was lower for dynamic than for static search, with sensitivity decreasing as set size increased. Unlike in Experiment 1, however, there was one significant interaction: Search Type×Set Size, F(2, 22) = 8.74, p = .002, η_g = .07; no other interactions were significant (all ps > 0.1. The Search Type×Set Size interaction was because d′ decreased dramatically with increasing set size in dynamic search, but not in static search (see Fig. 5b), suggesting observers were more ready to accept highly uncertain responses in dynamic (but not in static) search as set size became larger.

The ANOVA on the response-bias parameter C also revealed all main factors to be significant: search type, F(1, 11) = 12.7, p = .004, η_g = .09, set size, F(2, 22) = 7.02, p = .004, η_g = .06, and reward, F(1, 11) = 24.2, p < .001, η_g = .3. Participants adopted a more liberal criterion (i.e., a tendency to respond “target present”) for dynamic relative to static search, and for small set relative to large set sizes. Further, reward associated with correct “present” responses, compared with correct “absent” responses, shifted response criteria towards liberal. There were also two significant interactions: Search Type×Set Size, F(2, 22) = 6.55, p = .006, η_g = .04, and Search Type × Reward,F(1, 11) = 23.17, p < .001, η_g = 0.24, mainly attributable to the differential reward effects between static and dynamic search: Reward only slightly influenced response criteria in static search, but had a stronger effect on dynamic search (more liberal with reward to target presence and more conservative with reward to target absence; see Fig. 5c). The lesser influence of reward on response criteria in static search is likely owing to a strategy of exhaustive search through static displays with small set sizes (<16 items). Accordingly, false-positive and miss responses were relatively rare in static search.

In summary, reward had differential effects on dynamic versus static search. Reward of correct target-present responses greatly enhanced discrimination sensitivity in static, but not in the dynamic, search. This suggests that, in static displays, discrimination of (attentionally) selected items may be enhanced by reward-induced postselective processing (identity checking), while this enhancement cannot work in dynamic displays, in which postselective checking is interfered by the abrupt item displacements occurring every 110 ms. In addition, in dynamic search, d′ was reduced especially as set size increased, consistent with the pattern in Experiment 1. This caused the error (false-alarm and miss) rates to increase as set size increased and, associated with this, to flatten the search slopes.

Experiment 3

In Experiment 3, the task difficulty was increased by making the distractor L look more like a T. Figure 6 presents the mean correct RTs, along with the error rates, as a function of set size, separately for target-present and target-absent trials, and for the dynamic and static search conditions. Inspection of Fig. 6 suggests that the pattern of RTs resembles that in Experiment 1, though the mean RTs were generally slower in Experiment 3. The search slopes were similar in dynamic search, while the target-absent slope was steeper than target-present slope in static search. A three-way repeated-measures ANOVA revealed all three main effects to be significant: set size, F(2, 22) = 118.2, p < .001, η_g = .14, target, F(1, 11) = 102.8, p < .001, η_g = .36, and search type, F(1, 11) = 26.05, p < .001, η_g = .13. Further, except for the Target×Display Type interaction, F(1, 11) = 2.2, p = .16, η_g = .002, all other two-way and three-way interaction were significant (all ps < .001).

Fig. 6

Results for Experiment 3. Mean correct RTs (lines) and mean error rates (bars), with associated standard errors, as a function of display size, separately for target-present and target-absent trials, and for the dynamic and static search conditions. (Color figure online)

As with Experiment 2, further analysis was carried out on the search slope, discrimination sensitivity, and response bias measures. Figure 7a depicts the mean search slopes as a function of search type and target. Both main effects were significant, target, F(1, 11) = 77.2, p < .001, η_g = .42; search type, F(1, 11) = 52.2, p < .001, η_g = .45, as well as the interaction, F(1, 11) = 20.9, p < .001,η_g = .32. The latter was mainly caused by the greatly increased slope in the static-search target-absent condition. By contrast, there was no difference in slopes between the target-present and target-absent conditions in dynamic search, F(1, 11) = 0.65, p = .43, η_g = .035, BF=0.52, consistent with Experiments 1 and 2, and no difference in the target-present slopes between static and dynamic search, F(1, 11) = 2.61, p = .13, η_g = .069, BF=1.0, consistent with Experiment 1.

Fig. 7

a Mean search slopes (ms/item), with associated standard errors, in Experiment 3. b Target-present/absent discrimination sensitivity d′, with associated standard errors, and c response criterion C, with associated standard errors, as a function of display size, separately for the dynamic and static search conditions. (Color figure online)

Analysis of the sensitivity parameter d′ revealed discrimination sensitivity to be higher in static relative to dynamic search, F(1, 11) = 139.3, p < .001, η_g = 0.58, and there was a general decrease in sensitivity as the set size increased, F(2, 22) = 42.86, p < .001, η_g = 0.16. The interaction between search type and set size was also significant, F(2, 22) = 4.58, p = .022, η_g = 0.04, which is consistent with Experiment 2.

An ANOVA on the response-bias parameter C again revealed participants to respond more liberally in dynamic as compared with static search, F(1, 11) = 32.6, p < .001, η_g = .28. Unlike the strong liberal bias in Experiment 1, however, the response bias was relatively neutral (i.e., close to zero [set-size 8: BF = 0.30, set-size 12: BF = 0.40, set-size 16: BF = 0.37]) in the dynamic search condition of Experiment 3. This might be owing to the fact that participants received error feedback in Experiment 3 (but not in Experiment 1), permitting them to adjust their decision criteria to attain more balanced error rates between target-present and target-absent trials. Note, though, that the difference in response bias between Experiments 1 and 3 was not statistically significant, F(1, 21) = 3.46, p = .077, η_g= 0.10; and, overall, the relative bias in the dynamic versus the static search condition did not change. In summary, increasing the task difficulty did not change the overall pattern of sensitivity and response bias effects, nor did it alter the slope ratios. In absolute terms, though, the slope and response bias (C) parameters were numerically increased compared with Experiment 1.

The stopping rule and the dynamic search model

To further examine, in model terms, why the search RT slopes in the dynamic target-absent condition were close to those in dynamic target-present condition, we adopted the multiple-decisions model (Wolfe & Van Wert, 2010). This model envisages multiple loops of item selection and decision processes, with a quitting process that controls the exit from the loop (see Fig. 8a for an illustration). The original model assumes that each time, a single item is selected and processed. To be more general and “ecologically valid,” here we used fixation-based item selection, as advocated by Hulleman and colleagues and supported by eye-tracking data (Hulleman & Olivers, 2015; Young & Hulleman, 2013). That is, an observer samples one or a few (N_i) items within the visual span (also known as the functional viewing field [FVF]), and makes a two-alternative forced-choice (2AFC) decision about the sampled items. It should be noted that each step of decision-making has its own decision variable (from the sample) and response criterion. For simplicity, we assume the response criterion does not change within a trial but may vary across trials; and the final behavioral results we observed derive from these multistep decisions combined.

Fig. 8

a Schematic of the quitting process. b Accumulation of quitting variable T_qover each step of the selection-and-detection process. A decision variable d_v is sampled from a selected patch and compared with the decision criterion C. If d_v is above the criterion, a positive response is made; otherwise, the likelihood of target absence d_Δ(measured by the distance of the decision variable from the decision boundary) is accumulated to the quitting variable T_q. When this reaches the quitting threshold T_s, a negative response is made

Like the original multiple-decisions model (Wolfe & Van Wert, 2010), we assume that responses are made when the target is found or an accumulating quitting variable reaches a threshold level. As long as the quitting variable has not yet reached threshold, we assume participants sample a few items within each frame of the dynamic search display and make a decision about whether one of the sampled items is the target (see Fig. 8b). However, whereas the original model assumes that the quitting process is a pure diffusion process, independent of decisions about individual samples (i.e., the evidence accumulated in favor of quitting with a target-absent decision after each individual sample is independent of the decision evidence for that sample), our model version assumes that each individual decision adds a certain amount of information to the quitting variable, depending on the likelihood of “target absence.” This contrasts with the previous model (Wolfe & Van Wert, 2010), according to which the amount of search time (even though the decision variable is accumulated in a random-walk-type fashion) is the sole factor for quitting. In our model, when a given sample of items consists of distractors only, the decision variable favors “target absence” over “target presence,” with this balance of evidence contributing to the quitting variable. On the other hand, if the decision variable reaches the “target-present” decision boundary, a “target-present” response will be triggered and search will be terminated (see Fig. 8a). Using signal detection theory, we assume a noisy sample of evidence d_v ∼ N(μ, σ) is drawn from each step of item selection, where μ = 0 if the selected patch does not include the target, and μ = μ_P if it does contain the target. The decision boundary is the decision criterion C. If d_v is greater than C, a positive response is issued. Otherwise, the information about the likelihood of “target absence” contributes to the quitting variable. There are many ways to construct this likelihood. A simple and intuitive way is to use the distance to the decision boundary d_Δ = C − d_v as the information for the quitting variable (see Fig. 8b).

The quitting variable accumulates each step of likelihood of “target absence” until it reaches a quitting threshold T_s, that is:

$$ {T}_q=\underset{T}{\mathit{\min}}{\sum}_{t=1}^T{d}_{\varDelta}^{(t)}>{T}_s,\mathrm{for}\ \mathrm{all}\ {d}_v^{(t)}<C. $$

(1)

To better understand how the quitting threshold was set as a function of the set size and the reward manipulation, we selected the target-absent trials (including error trials) from Experiments 1 and 2 (recall that Experiment 3 had yielded similar results to Experiment 1) and estimated the RT distributions as a function of set size and reward. Figure 9a shows typical patterns from two observers, and Fig. 9b depicts a typical example of the reward effect on the RT distributions. As can be seen from Fig. 9, the RT distribution shifted rightward for some observers (but not for others) when the set size increased. This pattern suggests that some observers did indeed use timing or counting models (Wolfe, 2012; Wolfe & Van Wert, 2010) to set a quitting threshold. Moreover, reward assigned to correct target-absent responses greatly shifted the RT distribution leftward. Based on these observations, our model version assumes that the quitting threshold T_s is a linear function of the set size and a step function of the reward manipulation:

$$ {T}_s=a+b\cdotp N\pm {\varDelta}_r, $$

(2)

where N is the set size and Δ_r a shift based on the reward manipulation. Δ_r is subtracted if reward is assigned to correct target-absent responses and added if it is assigned to correct target-present responses.

Fig. 9

a RT distributions as a function of set size from the target absent condition in Experiment 1. The probability density functions of two typical observers (#7 and #11) are shown in solid and dashed lines, respectively, for three different set size. b RT distributions as a function of set size and reward manipulation (indicated solid and dashed lines) in the target-absent condition of Experiment 2, for a typical observer. (Color figure online)

In addition, based on the findings of Experiment 2, we assume that the reward manipulation also changes the decision criterion, that is:

$$ C={C}_0\pm {\varDelta}_{c,}, $$

(3)

where C₀ is the baseline decision criterion for the dynamic search and Δ_c the shift due to the reward manipulation. The decision becomes more liberal when the reward is applied to target-present trials, and more conservative when applied to target-absent trials.

The model has eight parameters. Four are used for selection and decision making: N_i, μ_p, C₀, and Δ_c. Parameter N_i specifies how many items are sampled at a given time (i.e., the size of FVF). Parameter μ_P is the average strength of the decision signal for decisions about a sample that includes the target. The standard deviation of the strength of the decision signal is assumed to be the same whether or not a target is sampled, and since one parameter could be set arbitrarily (i.e., for any change of this parameter, the other parameters could be scaled such that the model predictions are the same as before the parameter change), we fixed the standard deviation σ to 1. C₀ and Δ_c determine the decision criterion (see Equation 2). Three parameters (a, b, and Δ_r in Equation 1) determine the quitting threshold and the way it depends on set size and reward. Finally, a nondecision-time parameter τwas added to the reaction time for each condition.

We fitted the model parameters to the data aggregated across participants. For Experiments 1 and 3, we only use six parameters (i.e., we did not include the reward-related parameters Δ_r and Δ_c). Figure 10 shows, separately for Experiment 1 (a) and Experiment 3 (b), the empirical results (symbols) and the model predictions (lines) for the mean RTs, sensitivity d′, and response bias C. As can be seen, the model captured the experimental results very well, all within the 95% confidence intervals.

Fig. 10

The model predictions for Experiments 1 (a) and Experiment 3 (b). Left panel: Model predictions (lines) of the mean RTs (symbols) as a function of set size, separately for the target-present and target-absent conditions (denoted by circles and triangles, respectively). Middle panel: Model predictions of the discrimination sensitivity d′ as a function of set size. Right panel: Model predictions of the response criterion C as a function of set size. Error bars represent the 95% confidence intervals

The predictions from the model are also closely in line with the behavioral data from Experiment 2. As can be seen from Fig. 11, the model predicts the search slopes for the target-absent and target-present conditions, as well as the discrimination sensitivity d′ and the criterion C.

Fig. 11

a Mean reaction times (circles) and model predictions (lines) for reward assigned to correct target-absent (left) and correct target-present responses (right), respectively, in Experiment 2. b Discrimination sensitivity d′ and model predictions for the reward to target-present and reward to target-absent responses in Experiment 2. c Response criterion C and model predictions for the reward to target-present and reward to target-absent responses in Experiment 2. Error bars represent the 95% confidence intervals. “RA” denotes reward for correct target-absent responses, and “RP” reward for correct target-present responses

The fitted parameters are listed in Table 1. As can be seen from Table 1, the N_i estimates were the same across all experiments. A possible reason for the relatively stable N_i estimates in dynamic search is that the sample size was constrained by the same display reshuffling rate in all experiments, with a new sample of items being made available automatically every 110 ms, whether or not the participant was ready to process it. This may have made participants sample new items faster than they would otherwise have done; also, the constant reshuffling of the display might have blocked participants’ own (internal) regulation of the sampling rate, which they would have controlled otherwise (e.g., adjusting the sampling rate dependent on task difficulty). Note that the current N_i estimate in dynamic search (of N_i = 3 items) is consistent with previous studies (Geyer et al., 2007; von Mühlenen et al., 2003), in which performance on a dynamic search task did not differ between a condition in which only three items were shown at a time, compared with when all items were available.

Table 1 The parameters obtained from the best fits for Experiments 1–3

Task difficulty influenced nondecision time τ and the strength of each step decision variable (determined by μ_p). μ_p was the smallest in Experiment 3, reflecting the reduced difference, compared with Experiments 1 and 2, between the internal representation of the target (i.e., T) and distractor (L) shapes. μ_p was also somewhat higher in Experiment 2 compared with Experiment 1. This might reflect the effect of reward on perceptual learning: Reward assigned to correct responses may have led participants to sharpen the required target/distractor discrimination, compared with when there was no reward (see also Geng, Di Quattro, & Helm, 2017, for a report of target template sharpening in response to increasing competition from target-similar distractors). The extended “nondecision time” with increased task difficulty might reflect a slowed response decision after sampling a patch containing a target candidate (we come back to this point in the General Discussion). By contrast, the payoff manipulation shifted the decision criterion (C₀ ± Δ_c) and the quitting threshold (T_s = a + bN ± Δ_r). Comparing the quitting thresholds among the three experiments, the function relating the quitting threshold to set size was flattened as a result of the reward manipulation (the slope b of 0.5 in Experiment 2 was less steep than the slopes of 1.0 and 0.8 in Experiments 1 and 3, respectively): observers were more willing to quit search with larger set sizes under reward conditions. This might reflect the influence of an urgency signal. That is, participants may have been unwilling to spend more than a certain amount of time on any trial; so, under conditions in which a greater amount of time would need to be spent for accurate performance, they may become more willing to quit even without having accumulated sufficient evidence. This would predict target-absent slopes to become less steep when task difficulty increases and search takes longer, because the influence of the urgency signal increases and participants are more willing to quit early, in particular with larger set sizes. This could explain why parameter b was somewhat smaller with the more difficult task implemented in Experiment 3, compared with that in Experiment 1. Similarly, in Experiment 2, one of the effects of reward may have been to increase the sense of urgency, so as to maximize the average amount of reward gained per time unit.

More interestingly, the model suggests that two factors drive the target-present and target-absent slopes to be similar: The first is the dependence of the quitting threshold T_s on set size N: T_s increases slightly as N increases (though it was not doubled when set size increased from eight to 16 items). That is, observers follow an intuitive stopping rule: they wait somewhat longer when the set size is larger, but not for as long as would be required theoretically (see footnote 1) to keep the miss rate and false-alarm rate equal across the various set sizes. In other words, observers did trade the miss rate for an early search termination. The second major factor is that the information for quitting is accumulated based on the evidence of “target absence” from patches sampled in each step, which is different from previous quitting models based on static search (Moran et al., 2013; Wolfe & Van Wert, 2010). Both factors contribute to the even slope ratios we observed in dynamic search.

It should be noted that, as modeled here, the quitting process is also applicable to static search; in fact, it predicts the behavioral data quite well (see Supplementary 1). The only changes that needed to be introduced concern (i) the selection probability of the target over multiple selection and decision steps, which depends on the assumption of search being memory guided, and (ii) quitting upon exhaustive scanning. Given the very low error rates for static search, the model for this type of search comes close to an exhaustive-search model, as the quitting threshold is set high enough to yield near-error-free performance (see Supplementary 1). Bear in mind that parameter N_i for static search was estimated per (sampling) time units of 110 ms, to ensure comparability with dynamic search, so the estimate of N_i = 1 item in static search ought to be interpreted with caution: The true sample size may well be larger when the sampling interval is made longer (see details in Supplementary 1). It would be interesting in future studies to apply the present model to search scenarios with low target prevalence or foraging, when exhaustive search is not an available option.

General discussion

Flat slopes in dynamic search

The aim of the present study was to elucidate the causes of the (unexpectedly) flat search RT slopes in Horowitz and Wolfe’s (1998) dynamic search scenario. Indeed, their original finding proved highly replicable: for target-present trials, the slopes we observed for dynamic search were similar to those for static search. A novel finding was that, in a standard, nonrewarded T versus Ls search task, the slopes were not significantly different between target-present and target-absent trials in dynamic search, whereas the target-absent:target-present slope ratio remained above 2 in static search. The latter was predicted by classic FIT (Treisman, 1986; Treisman & Gelade, 1980) and the guided search model (Wolfe, 1994; Wolfe & Horowitz, 2017). However, these models fail to provide a ready account for the flat slopes in dynamic search, and, notably, the finding that the target-absent slope was even flatter (in dynamic search) when reward was assigned to correct target-absent responses.

The reason for the relatively flat search slopes on target-absent trials has largely been neglected in prior research, partly due to the fact that explaining how search is terminated on target-absent trials is, arguably, even harder for search scenarios with dynamic (as compared with standard, static) displays (Horowitz & Wolfe, 1998; Wolfe, Palmer, & Horowitz, 2010). If participants do not have prior knowledge of the target-present:target-absent ratio, they cannot acquire all the information necessary to make a decision when only distractors have been sampled. This is because from having encountered only distractors during scanning, one cannot infer the probability of target presence (e.g., the real target prevalence might be low). The only way for participants to infer the probability of target absence on a given trial is by combining some form of prior knowledge of the frequency of target absence in the experiment (across all experiments, participants were told that the target presence and absence were equally likely) and the probability of not having hit upon the target after t samples. Based on these two pieces of information, participants can gauge the uncertainty that the target is present but has not yet been sampled, which decreases over the time. That is, participants have to trade off between waiting to sample more items and making a decision with a degree of uncertainty. Observers often encounter such trade-off problems when exhaustive search cannot be applied, such as searching for an unknown number of targets among unknown numbers of distractors (e.g., looking for dangerous items at the airport checkpoint). Those searches do require a termination process.

The search termination process

Previous studies of search termination have focused mainly on the influence of target prevalence (Fleck & Mitroff, 2007; Wolfe et al., 2007; Wolfe & Van Wert, 2010). When targets are rare, participants shift their response criteria, speeding target-absent responses and increasing target miss rates (Fleck & Mitroff, 2007). Although target prevalence was equal by design for the dynamic and static search conditions (i.e., 50%) in the present and in Horowitz and Wolfe’s original experiments, the target being selected within a given time frame is effectively less likely in dynamic, as compared with static, displays, owing to the reshuffling of the display items in dynamic search and assuming memory plays a role in static search. This is one of the main factors that makes overall search time slower in dynamic than in static search. In addition, the probability of the target being selected becomes lower as set size increases. As a consequence, the subjective probability of target selection would be low, which brings about an increase of the quitting threshold—witness the increase in the stopping time with increasing set size (in the modeling section above). Of note, however, the stopping time was only slightly increased (rather than being doubled when the set size was doubled, from, say, eight to 16 items), which produced an increase of the miss rate with increasing set size. Interestingly, this behavior is very much like that observed in search for a low-prevalence target (Fleck & Mitroff, 2007; Wolfe et al., 2007), in which observers often stop earlier.

Search termination has been incorporated explicitly in recent multistage search models (Moran et al., 2013; Wolfe, 2012; Wolfe & Van Wert, 2010). For example, Wolfe and Van Wert (2010) assumed that search termination involves a drift-diffusion process, like a timer with random fluctuation gauging the tolerance of the maximum search time; Moran et al. (2013), by contrast, suggested that the weight of the quit unit, as compared with the other weights associated with the search items, increases over time. Both models implemented the cost of prolonged search time in their quitting process using different approaches. Similar implementations, such as a cost for delayed decisions or an urgency signal, have also been proposed in recent value-based decision-making (Tajima, Drugowitsch, & Pouget, 2016) and collapsing-boundary drift-diffusion models (Hawkins, Forstmann, Wagenmakers, Ratcliff, & Brown, 2015). Note, though, that these models only consider the dimension of time (in various forms of “urgency to quit”) in the quitting process. The model we have developed here considers not only the urgency to quit, but also decision information—the likelihood of a negative (i.e., “target-absent”) response—which is accumulated in the quitting decision variable.

That some kind of decision information is being accumulated, rather than merely an urgency signal, is in line with a study by Peltier and Becker (2017). They argued that high false-alarm rates in search tasks with high target prevalence are, at least in part, explained by participants sometimes responding “target present” as a guess, even though they have not perceived any item looking like the target (i.e., they did not mistake a distractor for the target). Peltier and Becker (2017) showed that false-alarm rates depended less on target prevalence when participants were able to gather as much information as they wished before making a response, compared with when the search was terminated early (automatically) if participants had not issued a response after a certain number of fixations. Importantly, false-alarm rates were lower under unrestricted display conditions compared with trials performed under time pressure (i.e., with a time limit), on which participants managed to terminate the search themselves (i.e., prior to the automatic termination). This pattern is consistent with the idea that participants accumulate evidence across multiple fixations and that the guessing rate depends on the amount of accumulated information. In our model, the accumulated information is used only for deciding when to stop (and respond “target absent”), rather than for occasionally making target-present guesses. However, the model could easily be made to stop early and guess “target-present/target-absent” based on the strength of the target-absent evidence accumulated thus far.

Further, just like Wolfe and Van Wert’s (2010) model, our model assumes that participants sample one or a few items at a time and, for each sample, make a decision about whether it contains a target, based on whether a noisy decision signal is above some criterion level, and they keep sampling until sufficient evidence has been accumulated for a target-absent or target-present decision. However, our model differs from Wolfe and Van Wert’s (2010) in that we assume that the speed with which evidence accumulates towards the target-absent criterion is related to the signal underlying the decisions of whether a target is absent in the individual samples (of limited patches of items): Our model assumes that, after each sample in which no target was detected, the amount of evidence accumulated towards a target-absent decision depends on how far below the criterion level the decision signal in the given sample was (see Fig. 8). That is, evidence towards a target-absent response accumulates faster when the decision signal in an individual sample is far below criterion (in which case the certainty that a target was absent in the sample is high) compared with when it is close to criterion (in which case the certainty a target was absent is low). Note also that, for reasons of simplicity, our model assumes that the evidence accumulates linearly with the distance of the decision signal to the criterion. A more realistic assumption would be that the evidence from each sampled subset saturates at a certain upper bound (in a sigmoid fashion), because a single sample consists of only one or a few items and processing of this can therefore at best provide near certainty that the target is not present in the sampled patch. Nevertheless, the linear approximation already provides a good fit. The key parameters for our model to successfully reproduce the similar search RT slopes for target-absent and target-present trials in dynamic search are the stopping time and the quitting evidence (Equations 1 and 3). The model simulation suggests that the stopping time slightly increased as the set size increased, without reaching the theoretical stopping time (for maintaining a constant low miss rate). That is, observers traded the miss rate for the stopping time, effectively flattening the search slope for target-absent trials.

Influences of reward and task difficulty on dynamic search

As expected based on other work (Eckstein et al., 2010; Navalpakkam et al., 2010; Sohn & Lee, 2006), reward manipulations shift the decision criteria towards the rewarded response. This has been confirmed in Experiment 2 by the overall shifts of the RTs (see also Fig. 9b), as well as the shift of the decision criteria. Interestingly, reward did not change the RTs averaged across target-present and target-absent trials, indicating that reward assigned to target-present and target-absent responses, respectively, is equally effective. This led us to model the multistage decision criterion to be shifted equally by the reward manipulation (Equation 3), which successfully predicted the mean RTs and error rates (Fig. 11). Previous studies have reported that rewards also shorten the latencies of saccades towards rewarded targets (Navalpakkam et al., 2010; Sohn & Lee, 2006). Given that dynamic search involves more “sit-and-wait” saccadic patterns compared to static search, it would be interesting to investigate, in future studies, whether rewards have a differential impact on saccadic latencies between static and dynamic search.

It should be noted that in Experiment 2, decision sensitivity was not changed by the rewards. This is different from previous findings suggesting that reward can change the bottom-up saliency of reward-associated stimuli (Anderson, Laurent, & Yantis, 2011, 2012). For example, visual search has been reported to be slowed by the presence of a task-irrelevant item that had previously been associated with monetary reward (Anderson et al., 2011), indicative of involuntary attentional capture by the rewarded item. The effect of reward on “saliency” may arise at a preselective stage (the rewarded item may summon focal attention faster) and/or a postselective stage (verification that the attended patch contains a target may be expedited). However, given that reward-based enhancement of saliency would affect only one decision (e.g., postselective target identification) amongst the multiple sequential decisions in the multistage decision process, it would have little impact on the general decision sensitivity, as we observed here.

It is important to note that neither reward nor search difficulty changed the target-absent:target-present slope ratio in dynamic search back to 2 or above, as found for static search. The ratio was still close to or even below 1. As shown by Young and Hulleman (2013), item movement alone is not a critical factor for changing eye-movement behavior and search slope ratios. Young and Hulleman (2013) introduced random, but trackable, movements of search items (rather than abrupt changes of item locations as in dynamic search). They found that, while task difficulty changed the slopes, the target-absent:target-present slope ratios remained above 2 (Figure 2, Young & Hulleman, 2013). Kristjánsson (2000) also showed that it is not the abrupt change of search display, but rather the relocation of the items that matters. In his study, the search slope ratio remained above 2 when the items randomly (and abruptly) changed their orientation frame to frame while remaining at the same locations given that the set size was relatively small. In contrast, the slope ratio became close to 1 when the items were relocated (even to previously occupied locations), or set size was increased up to 56 items. Kristjánsson (2000) argued that relocating items effectively abolishes a memory-aided search strategy, in line with the arguments put forward by Klein (1988). Relocating items frame by frame is a key property of dynamic search. In all three experiments reported here, the search slopes for dynamic target-absent trials were equal to or shallower than the slopes for dynamic target-present trials. Although reward shifted the decision criteria and the quitting threshold, the relation of the quitting threshold to set size (i.e., the slope) remained below 1 (see parameters in Table 1). In fact, reward allocated to correct target-absent responses, compared with reward allocated to correct target-present responses, rendered the search slope even flatter for target-absent trials. This is because reward associated with target absence encouraged observers to quit with a negative response (see Fig. 5c), which then flattened the slope.

Increasing the task difficulty in Experiment 3 slowed the mean RTs in general, yet the absolute slopes did not differ between the target-absent and target-present conditions. The overall slowed responses were captured by the model in the increased “nondecision time” (τ), which may reflect a slower response decision after sampling a potential target candidate. Sun and Landy (2016) proposed a two-stage perceptual decision-making model, based on the results of a “cued-response” task. Participants had to judge the direction of motion in random dot kinematograms (RDKs), which were displayed for a variable time and then removed at the onset of an auditory cue; participants had to respond as quickly as possible after the cue. The time to decision after the cue decreased with increasing coherence of the RDK and with the time for which the RDK had been displayed prior to the cue—even though the stimulus was no longer available after cue onset, so that no further sensory evidence accumulation was possible. Sun and Landy (2016) interpreted this as evidence of a second stage of perceptual decision-making, after first stage of sensory evidence accumulation “until estimation precision reaches a threshold value” (p. 11259), the duration of which depends on the signal-to-noise ratio achieved in the first stage. A similar two-stage process may also be at work in the difficult dynamic search task (in which each display was reset/masked by the subsequent display), explaining why the reduced μ_p in Experiment 3 would be associated with a longer “nondecision time” τ. The reshuffling in dynamic search displays makes it impossible to take a closer look to confirm whether a target candidate is a true target at the first stage of sampling, which in turn delays the decision in the second stage. It should be noted, though, that the change in task difficulty did not impact the relation to set size, which is critical for the search slope. A similar explanation for the overall longer reaction times in the dynamic condition was proposed by Horowitz and Wolfe (1998), who suggested that the longer mean RTs in the dynamic condition may “reflect subjects’ decreased confidence in their responses” because, unlike with static displays, the stimulus is not available for confirmation after the participant believes he or she has found it.

Of note, the model we developed here primarily focused on the search termination process involved. It predicts close to 1:1 search RT slopes for target-absent versus target-present trials in dynamic search, and 2:1 search slopes in static search (see Supplementary 1), but still falls short of explaining why the slopes for target-present trials were similar for the dynamic and static search conditions. Assuming (with Horowitz & Wolfe, 1998) that search was amnesic in dynamic search, but memory aided in static search would not help (given that observers may still use spatial memory even in dynamic search, harming performance; see, (e.g., Kristjánsson, 2000). Thus, one possible explanation remaining might be that observers use the stopping time from the static search as a reference for terminating the dynamic search, given that the static and dynamic search displays were essentially the same and both types of display were tested in randomly interleaved fashion within the same session. However, modeling both dynamic and static searches together would require assumptions about the sequential sampling probability (i.e., the size of the FVF and the probability of revisiting old locations) during the multistage selection-and-decision process, for which additional behavioral data, such as eye-movement records (Geyer et al., 2007; Young & Hulleman, 2013), would be needed. This must await further investigation.

Conclusion

In summary, we found that, unlike the search RT slopes in static search, the slopes in dynamic search were relatively equal for target-present and target-absent trials. Also, manipulation of reward or task difficulty did not change the slope ratio under conditions of dynamic search. The critical factors that cause the slopes to be similar in dynamic search are, first, that the stopping threshold increases slightly as the set size increases and, second, that the accumulating decision information for quitting is based on the likelihood of target absence in each “selection-and-decision” step.