How to estimate how well people estimate: Evaluating measures of individual differences in the approximate number system

Chesney, Dana; Bjalkebring, Par; Peters, Ellen

doi:10.3758/s13414-015-0974-6

How to estimate how well people estimate: Evaluating measures of individual differences in the approximate number system

Published: 03 September 2015

Volume 77, pages 2781–2802, (2015)
Cite this article

Download PDF

Attention, Perception, & Psychophysics Aims and scope Submit manuscript

How to estimate how well people estimate: Evaluating measures of individual differences in the approximate number system

Download PDF

Dana Chesney¹,
Par Bjalkebring^1,2 &
Ellen Peters¹

3867 Accesses
18 Citations
2 Altmetric
Explore all metrics

Abstract

At a glance, one can tell that there are more individual fruits in a pile of 100 apples than in a pile of 20 watermelons, even though the watermelons take up more space. People’s ability to distinguish between such nonsymbolic numerical magnitudes without counting is derived from the approximate number system (ANS). Individual differences in this ability (ANS acuity) are emerging as an important predictor in research areas ranging from children’s understanding of arithmetic to adults’ use of numbers in judgment and decision making. However, ANS acuity must be assessed through proxy tasks that might not show consistent relationships with this ability. Furthermore, practical limitations often confine researchers to using abbreviated measures of this ability, whose reliability is questionable. Here, we developed and tested several novel ANS acuity measures: a nonsymbolic discrimination task designed to account for participants’ lapses in attention; three estimation tasks, including one task in which participants estimated the number of dots in a briefly presented set, one in which they estimated the ratio between two sets of dots, and one in which they indicated the correct position of a set of dots on a “number-line” anchored by two sets of dots, as well as a similar number-line task using symbolic numbers. The results indicated that the discrimination task designed to account for lapses in participants’ attention holds promise as a reliable measure of ANS acuity, considered in terms of both internal and test–retest reliability. We urge researchers to use acuity measures whose reliability has been demonstrated.

Circling around number: People can accurately extract numeric values from circle area ratios

Article 16 March 2022

On the linear representation of numbers: evidence from a new two-numbers-to-two positions task

Article 02 August 2018

The log–linear response function of the bounded number-line task is unrelated to the psychological representation of quantity

Article 20 April 2017

Numeracy and individual differences

A growing body of literature has demonstrated that individual differences in numeric ability predict a diverse range of life outcomes. People who are better at math achieve higher educational attainment, better health, and greater economic success (Adelman, 2006; Blanton & Kaput, 2005; Bynner & Parson, 2009; National Council of Teachers of Mathematics, 2000; National Research Council, 2001, National Mathematics Advisory Panel, 2008; Peters, Meilleur, & Tompkins, 2013; Reyna, Nelson, Han, & Dieckmann, 2009; Smith, McArdle, & Willis, 2010). It has been estimated that numeracy issues in the United Kingdom cost £2.4 billion (about U.S. $4 billion) per year in lost productivity (Callaway, 2013). Moreover, people with greater numeric ability perform better on a diverse set of judgment and decision-making tasks (Peters, 2012; Peters, Hart, Tusler, & Fraenkel, 2014; Peters et al., 2006; Sinayev & Peters, 2015).

Numeric ability, however, is not limited to symbolic math ability (Peters & Bjalkebring, 2015; Peters, Slovic, Västfjäll, & Mertz, 2008; Schley & Peters, 2014). Rather, it is a collection of interrelated perceptual and cognitive skills that allow individuals to transform, evaluate, and use numeric information. These faculties not only include understanding of symbolic numbers and fluency with arithmetic and higher-order mathematics, but also include the ability to evaluate and compare nonsymbolic numerical magnitudes (e.g., [ ::: ] vs. [ :::: ]; Cordes, Gelman, Gallistel, & Whalen, 2001; Dehaene, Dehaene-Lambertz, & Cohen, 1998; Kaufman, Lord, Reese, & Volkmann, 1949; Taves, 1941; Whalen, Gallistel, & Gelman, 1999). In this article, we are primarily concerned with measures of this latter component of numeric ability: the ability to evaluate nonsymbolic numerical magnitudes—the approximate number system (ANS).

Nonsymbolic numerical magnitudes

Sets, such as this set of dots [ ::: ], have a particular numerical magnitude, in this case “6.” The numerical magnitudes of sets are nonsymbolic. As humans, we have the ability to represent these numerical magnitudes exactly using words (e.g., “six”) or symbols (e.g., “6”). However, similar to the way we can perceive the length of two lines and tell which is longer without considering their precise length in inches, we have the ability to perceive and compare the numerical magnitudes of sets using analog (continuous) representations of numerical magnitude, without assigning a verbal or symbolic label to those perceived magnitudes. People are able to compare and evaluate the nonsymbolic numerical magnitudes of sets ranging up to many hundreds of items without counting (Taves, 1941), and without necessarily linking these values to a symbolic number (Kaufman et al., 1949). For example, one can often tell at a glance which of two bunches of grapes has more fruit, without needing to establish exactly how many grapes are in each bunch. Humans are not alone in this skill (Dehaene et al., 1998). The ability to perceive nonsymbolic numerical magnitudes of such sets is ubiquitous in the animal kingdom, having been seen for such diverse creatures as rats (Meck & Church, 1983), chickens (Rugani, Regolin, & Vallortigara, 2007), monkeys (Cantlon & Brannon, 2006), and beluga whales (Abramson, Hernández-Lloreda, Call, & Colmenares, 2013).

It is well established that the perception of nonsymbolic numerical magnitudes obeys Weber’s law (Cordes et al., 2001; Dehaene et al., 1998; Mechner, 1958; Meck & Church, 1983; Whalen et al., 1999). As is typically the case for magnitude perception (see Kingdom & Prins, 2010), nonsymbolic numerical magnitudes are not perceived exactly. Rather, the numerical magnitudes perceived from a nonsymbolic numerical stimulus (e.g., a set of dots) are approximate, with a normal or quasi-normal distribution around a mean value, which may itself be biased. Consequently, the ability of the ANS to distinguish between the numbers of items in two sets is dependent on the amount of overlap between the distributions of the numerical magnitudes perceived from these sets. According to Weber’s law, discriminability (and thus the “width”—i.e., standard deviation—of the implicit perceived magnitude distributions) is proportional to the stimulus magnitude. Consistent with this, the overlap in the distributions of any two perceived numerical magnitudes is thought to depend on their ratio (or log distance), rather than on the arithmetic distance between them.

To illustrate, consider a common scenario in which a participant in a psychology study is shown two sets of dots and asked to say which is more numerous. The overlap of the numerical magnitudes that the participant would perceive from 13 and 10 dots is thought to be the same as the overlap of the numerical magnitudes that the participant would perceive from 130 and 100 dots, because the numbers have the same ratio. This leads to both size and distance effects in nonsymbolic numerical magnitude discrimination. Within the same range, it is easier to distinguish nonsymbolic numerical magnitudes that are more distant from each other than to distinguish those that are closer together (distance effect: it is easier to distinguish 13 from 10 dots than to distinguish 12 from 11 dots), because increasing the arithmetic distance also increases the ratio. Also, it is easier to distinguish smaller than to distinguish larger nonsymbolic numerical magnitudes at the same distance (size effect: it is easier to distinguish 13 from 10 dots than to distinguish 83 from 80 dots), because the ratio between the smaller-valued pair is bigger than the ratio between the larger-valued pair, despite having the same arithmetic distance. Consequently, numerical magnitude judgments conducted by the ANS yield standard psychophysical functions (Whalen et al., 1999; see Kingdom & Prins, 2010), such that the likelihood that an individual will successfully discriminate between two numerical magnitudes increases curvilinearly from chance to asymptote at or near 100 % accuracy as the ratio of the larger to the smaller numerical magnitude increases. Similarly, reaction times decrease with the comparison ratio. Neuro-activation patterns analogous to these analog numerical magnitudes have been detected in humans via neuroimaging (Piazza, Izard, Pinel, Le Bihan, & Dehaene, 2004) and in monkeys via single-cell recordings (Nieder & Miller, 2003, 2004).

We note that debate exists regarding the nature of the mechanism underlying nonsymbolic numerical magnitude judgments. Some researchers posit tally-like systems that, via various methods, essentially “count” the items in a perceived set (e.g., Dehaene & Changeux, 1993; Meck & Church, 1983). Others note that continuous-extent features such as individual item size, total area, and density are confounded with numerical magnitude, such that the total number of items in a set can be deduced from sufficient continuous-extent information (e.g., given that the total area of a set of items is 4 cm² and the average area of an item is 0.33 cm², there must be 12 items). These researchers posit that various perceptual quantity cues are integrated to yield numerical magnitude perception (Gebuis & Reynvoet, 2012). Whatever the mechanism, mounting evidence exists that numerical magnitude information is extracted from sets automatically and without conscious effort, and this perceived numerical quantity information can influence our actions separately from other quantity information (e.g., total area; for a review of the infant literature, see Cantrell & Smith, 2013). For example, nonsymbolic numerical magnitude has been shown to have a Stroop-like impact on people’s ability to respond to area information, facilitating area responses when the area quantity (total area) and numerical quantity (total number of dots) are congruent, and inhibiting area responses when the area and numerical quantities are incongruent (Hurewitz, Gelman, & Schnitzer, 2006). The present article is agnostic as to the process by which numerical magnitude assessments are made. We focus instead on the precision of these assessments. The precision with which one can perceive nonsymbolic numerical magnitudes will henceforth be referred to as ANS acuity.

Individual differences in ANS acuity

The ability of the ANS to make numerical magnitude discriminations is thought to vary among individuals, such that some individuals can make faster and more accurate judgments with smaller ratios than other individuals can (Halberda & Feigenson, 2008). Again, as is typically the case for perceived magnitudes, this ANS acuity is defined by an individual’s “Weber fraction.” The ANS obeys Weber’s law (Halberda, Mazzocco, & Feigenson, 2008; Whalen et al., 1999), which is often interpreted as implying that the ratio between the standard deviation and the mean of a magnitude estimate (SD/M, its “coefficient of variation,” or CV) is constant. Put simply, the standard deviation of the distribution around an estimated magnitude is proportional to that magnitude’s mean. That proportion is, by definition, the Weber fraction (w) of the perceiver’s ANS. After accounting for bias, this w (equivalent to the constant CV) determines the variability in the representation of a particular numerical magnitude, the amount of overlap between any two represented numerical magnitudes, and how likely it is and how quickly it is that an individual will be able to tell two nonsymbolic numerical magnitudes apart. There are competing accounts regarding the mechanism underlying these behavioral phenomena (e.g., logarithmically compressed numerical magnitude representations with constant variability: Dehaene, Izard, Spelke, & Pica, 2008; Siegler & Opfer, 2003; or linearly spaced numerical magnitude representations with proportionally increasing variability: Cordes et al., 2001; Cantlon, Cordes, Libertus, & Brannon 2009; Gallistel & Gelman, 2000; Whalen et al., 1999). However, in all accounts, the smaller an individual’s w, the better that individual is at discriminating between nonsymbolic numerical magnitudes, because the numerical magnitude perceptions overlap less.

ANS acuity, objective numeracy, and judgments

Evidence also exists that individual and group differences in ANS acuity predict performance on tasks that involve numbers. For example, ANS acuity has been found to increase throughout childhood. Ten-month-olds typically cannot discriminate between the numerical magnitudes of two sets whose ratio is lower than 2/1 (e.g., 30 vs. 15 dots; w = 1), but 12-month-olds are able to discriminate numerical magnitudes whose ratio is as low as 3/2 (e.g., 30 vs. 20 dots; w = .5; see Cantrell & Smith, 2013, for a review). This acuity continues to increase through grade school (Halberda & Feigenson, 2008). These acuity increases parallel improvements in symbolic and language-based numerical understanding, since older children have more acute representations and better skills at counting and arithmetic tasks than younger children.

This correlation between ANS acuity and numerical skill is also seen within age groups. Better ANS acuity has been linked to better math skills in kindergarten (Gilmore, McCarthy, & Spelke, 2010) and to better performance on standardized tests of mathematical ability from kindergarten through sixth grade (Halberda et al., 2008), although the results in the literature have been mixed. Some researchers have attributed these mixed results to methodological issues (Chen & Li, 2014; De Smedt, Noel, Gilmore, & Ansari, 2013), with a recent meta-analysis indicating that the true correlation between ANS acuity and symbolic mathematical ability may be small (r = .2) among children and adults who have received formal mathematical education (Chen & Li, 2014). As a result, a much larger sample size is required than is typical for such studies, and this lack of power may explain the mixed results. It has also been suggested that a critical period may exist in which a child’s ability to estimate nonsymbolic numerical magnitudes aids the development of early numeric abilities (e.g., learning the values of symbolic numbers), after which math skills may develop separately from the ANS (De Smedt et al., 2013). In this case, correlations between ANS acuity and math ability in adults would be the result of past, rather than current, cognitive interdependence. However, recent research has demonstrated that practicing arithmetic with estimated nonsymbolic numerical magnitudes (set of dots) transfers to gains in symbolic arithmetic in educated adults (Park & Brannon, 2013, 2014). This finding indicates that ANS acuity remains connected to adults’ higher-order numeric abilities, such as understanding of symbolic numbers and mathematics.

The connection between ANS acuity and other numerical skills can be explained by a mapping between analog numerical magnitudes based on ANS perceptions and symbolic numbers. Humans, unlike other animals, have resources beyond the ANS to help them evaluate number. People can represent numbers verbally (e.g., the word “ten”) and with other symbols (e.g., “10”), and do so with much greater precision than the ANS can achieve. Using symbols, we can, for example, accurately judge numbers’ ordinality with near 100 % success, irrespective of the ratios between them (e.g., we can determine that 9 > 8, 99 > 98, and 9,999 > 9,998). However, evidence also exists that people do not rely solely on learned algorithmic or look-up-table procedures when evaluating symbolic numbers. Rather, people map these symbolic numbers to analog numerical magnitudes like those perceived by the ANS, and thereby invoke the same sorts of comparison processes used for analog numerical magnitude evaluation when considering symbolic numbers (Dehaene, Bossini, & Pascal, 1993; Moyer & Landauer, 1967). For example, people show distance effects when making judgments about symbolic numbers, even though such effects would result from neither look-up-based nor sequential-count-based comparison processes (Moyer & Landauer, 1967). One could, therefore, predict that performance on tasks involving symbolic numbers might be influenced by multiple processes, including individual differences in ANS acuity and the accuracy of the mapping between symbolic numbers and numerical magnitudes. In addition, higher-order mathematical skills, like those taught in schools, build off an understanding of symbolic numbers, which (as we discussed above) is linked to analog numerical magnitude representations.

Motivation of the present study

Assessments of mathematical skill are well understood, since they are similar to math tests one might take at school. Indeed, multiple researchers have worked to create short questionnaires that capture the distribution of this skill in a population (e.g., Cokely, Galesic, Schulz, Ghazal, & Garcia-Retamero, 2012; Lipkus, Samsa, & Rimer, 2001; Weller et al., 2013). However, metrics of individual differences in ANS acuity are less well investigated. Some tasks used to assess individual differences in ANS acuity have used symbolic numbers as the stimuli, rather than nonsymbolic numerical magnitudes (e.g., Holloway & Ansari, 2009; Peters et al., 2008; Sekuler & Mierkiewicz, 1977), even though the ANS does not directly perceive the values of symbolic numbers from the world. Rather, people learn to map symbolic numbers to analog numerical magnitudes stored in or generated from memory (see Dehaene & Cohen, 1998). Thus, performance on tasks involving symbolic numbers is likely influenced by multiple processes, including those reviewed above (e.g., ANS acuity and the exactness of symbolic-number mapping). Furthermore, practical limitations may lead researchers to make trade-offs between speed, accuracy, and reliability when choosing ANS acuity measures, leading them to use brief or abbreviated measures, whose reliability is not well established. For example, although two-option forced choice discrimination tasks are well regarded by psychophysicists for their ability to assess acuity in magnitude perception (Kingdom & Prins, 2010), such tasks typically require hundreds if not thousands of trials in order to attain good reliability. In contrast, the two-option forced choice task used by Halberda et al. (2008) had only 80 test trials, which may severely limit its reliability (Lindskog, Winman, Juslin, & Poom, 2013). Moreover, that task did not account for the rates at which participants have lapses in attention during such highly repetitive tasks (traditionally called the lapse rate; see Kingdom & Prins, 2010), causing them to give a response that is not based on the stimuli. This inattention can severely bias w estimates (Prins, 2012).

Furthermore, a widely used metric of ANS acuity is the “size” of the numeric distance effect (NDE: the increase in reaction time or decrease in accuracy for distinguishing values that are close to each other relative to those more distant from each other; see Price, Palmer, Battista, & Ansari, 2012, for a discussion). The NDE size metric has recently come under fire, with several studies questioning both its reliability and its ability to distinguish individual differences in ANS acuity (Gilmore, Attridge, & Inglis, 2011; Holloway & Ansari, 2009; Inglis & Gilmore, 2014; Lindskog et al., 2013; Maloney, Risko, Preston, Ansari, & Fugelsang, 2010; Price et al., 2012; Sasanguie, Defever, Van den Bussche, & Reynvoet, 2011). The measure is further complicated by the common use of symbolic magnitudes in the task, which may explain, in part, why NDE size has not reliably been shown to assess ANS acuity (it remains unclear whether it is a reliable measure of people’s ability to discriminate symbolic numbers).

In light of these facts, we believe it necessary to establish reliable ANS acuity metrics. In this article, we present five potential assessments of individual differences in ANS acuity and, unlike prior studies, report these assessments’ reliability. One assessment is a nonsymbolic discrimination task similar to that introduced by Halberda et al. (2008; see also Lindskog et al., 2013). Relative to these previous studies, we expanded the number of trials in order to increase reliability and to include a specific mechanism to gauge participants’ attention to the task. Measuring the rate of participants’ lapses in attention should allow us to separate the effects of effort from those of performance. Specific measures of such inattention are a new addition to the ANS measurement literature. The next three assessments are based on individual differences in performance on nonsymbolic estimation tasks developed by Chesney and Matthews (2012). Prior work with these tasks had only considered them in terms of group-level performance rather than as tools to detect reliable individual differences in ANS acuity. The final measure concerns the mapping of symbolic numbers, based on a task originally developed by Siegler and Opfer (2003). Thus, in the two studies of the present article, we go beyond the prior literature by (1) developing a metric that separates the effects of attention from performance, (2) evaluating a variety of short (and thus, easy to implement) methods thought to gauge ANS acuity in terms of internal (split-half) reliability and intertask correlations, and (3) providing evidence of test–retest reliability for the more promising measures. Thus, our studies provide useful tools to aid researchers in selecting valid ANS acuity measures whose reliability has been established and that best balance measure reliability and participant time.

One task is a 5- to 10-min, two-option, forced choice dot-discrimination task, specifically designed to allow calculations of w that account for the participant's lapse rate (i.e., the rate at which a participant’s attention to the task lapses) and to maximize the discriminability of ws found for average adults (typically estimated at about .11 or .22; Cordes et al., 2001; Halberda & Feigenson, 2008; Inglis & Gilmore, 2014; Lindskog et al., 2013; Pica, Lemer, Izard, & Dehaene, 2004; Price et al., 2012; Whalen et al., 1999). The next three tasks are 2- to 5-min estimation tasks, in which participants are asked to explicitly estimate the numerical magnitudes of dot sets. In the dot-line task, participants indicate the correct positions of dot sets on a “number-line” anchored by one dot on the left and a large set of dots on the right. In the dot-ratio task, participants estimate the ratio of two dot sets (e.g., :/:: → “1/2”; see Matthews & Chesney, 2015, and Matthews, Chesney, & McNeil, 2014, for discussions of nonsymbolic ratio perception). In the dot-number task, participants estimate the number of dots with a symbolic number that they think equals the number of dots displayed (e.g., :: → “4”). We note that the dot-ratio and dot-number tasks involve a symbolic number component that has the potential to interfere with these tasks’ ability to assess ANS acuity, despite the stimuli being nonsymbolic (sets of dots).

The final task was a 1- to 3-min symbolic-mapping (SMAP) task originally developed by Siegler and Opfer (2003), in which symbolic numbers were placed on a line. Accuracy on such tasks has been related to how much one values numeric objects (identified with symbolic numbers; e.g., a gamble in which you have a 50 % chance to win $9; Schley & Peters, 2014). Similar to the dot-ratio and dot-number tasks, the SMAP task involves a symbolic number component. As a result, performance on this task is likely influenced by more complex mechanisms, including the accuracy of analog numerical magnitude representations (Siegler & Opfer, 2003)—which are based on analog numerical magnitude perceptions (Dehaene et al., 1993; Dehaene & Cohen, 1998)—and the exactness of the mapping between symbolic numbers and these analog magnitudes. In addition, SMAP responses may be influenced by higher-order math skills, since values can be placed relatively accurately using a repeated bisection process. For example, one can place 80 on a 0–300 line by dividing both the upper anchor value (300) and the line by 2 twice, first to find the location of 150 and then to find 75, and finally by placing 80 slightly to the right of this location. Indeed, such bisection methods are used by grade school children (Barth & Paladino, 2011), and educated adults should be able to place such symbolic numbers relatively linearly on a number line (Siegler & Opfer, 2003). The correlation of SMAP performance with ANS acuity, therefore, may be attenuated by the use of these additional mechanisms.

In summary, four of the five tasks evaluated here use nonsymbolic stimuli, and as such participants must employ their ANS in order to perceive the stimulus magnitudes from the world. However, the responses for two of these four tasks involve symbolic numbers, and thus invoke the mapping between symbolic numbers and analog numerical magnitudes. The fifth task employs symbolic numbers as the stimuli. Thus, responses may be influenced by ANS acuity through these symbolic numbers’ mappings to analog magnitudes, but other mechanisms, such as line bisection, may interfere with this connection. In Study 1 (N = 247), we examined the split-half reliability of these measures and the correlations between them. In Study 2 (N = 39), we investigated the test–retest reliability of the dot-discrimination and SMAP tasks and the most reliable of the nonsymbolic dot-estimation tasks (dot-line) after a one-week delay. In addition to these potential assessments of ANS acuity, we included tasks to evaluate participants’ self-perceptions of their numeric skill (the Subjective Numeracy Scale [SNS]; Fagerlin, Zikmund-Fisher, Ubel, Jankovic, Derry, & Smith, 2007; Zikmund-Fisher, Smith, Ubel, & Fagerlin, 2007) and their abilities with traditional mathematics (the Objective Numeracy Scale [ONS]; Weller et al., 2013). To our knowledge, this study is the first to assess the correlations of individual differences in performance on multiple nonsymbolic estimation tasks with Weber fraction estimates as well as with symbolic number-line placement in educated adults. To foreshadow our results, the dot-discrimination task had both good internal reliability and good test–retest reliability, with no detected practice effects. It also provides an assessment of ability separate from that of effort.

Study 1

Method

Participants

The participants were 247 students at The Ohio State University (146 male, 101 female; mean age 19.0 years). They received course credit and a small snack as token compensation. One additional participant was excluded due to atypical behavior (e.g., distracted behavior, taking multiple snack breaks midsession) and a belief that the focus of the study was participants’ choice of snack.

Procedure

Each participant completed a set of computer-based tasks in a single 1-h session. All tasks were completed at desktop computers with mouse and keyboard inputs and a 56-cm monitor at a 16:9 aspect ratio. Participants were free to move their heads and eyes throughout the study and typically sat 60 cm from the monitor. Thus, the monitor typically subtended 44 deg of the participants’ visual field. They first completed two numeracy measures: the SNS, then the ONS. Next, they completed nonsymbolic estimation tasks developed by Chesney and Matthews (2012)—specifically, the dot-line, dot-ratio, and dot-number tasks described below. They then completed a SMAP task using the symbolic numbers corresponding to the numerical magnitudes of the stimuli used in the dot-line, dot-ratio, and dot-number tasks). Finally, after a short break, participants completed our dot-discrimination task—a modified version of the task developed by Halberda et al. (2008). They also completed several tasks unrelated to the present article, described in the online supplement. The tasks were ordered to minimize intertask interference. Demographic data, including self-reported SAT and ACT scores, were collected.

Measures

Subjective numeracy scale

Participants completed a self-assessment of numeric ability (Fagerlin et al., 2007). In this SNS, participants rated their self-perceived mathematical ability and preference for numbers on eight questions using six-point scales. Scores reflect the mean of these responses, with higher scores reflecting greater perceived ability. Scores on this task typically have medium to large correlations with objective tests of mathematical ability.

Objective numeracy scale

Participants completed an ONS (Weller et al., 2013; see Appendix 1). Scores reflect the total number correct out of seven recorded responses. We note that an eighth question was asked but not included in the score as responses on it failed to record.

Dot-discrimination task

We constructed the dot-discrimination task using the custom options available for the Panamath (2013) software (see Appendix 2 for the text of the custom values file). This task included substantially more trials than the version described by Halberda et al. (2008): 312 trials rather than 80. However, more subtle changes were also made, to enhance the task’s ability to assess individuals’ ws. In particular, we increased the number of different ratio levels presented from 4 to 13, and increased the number of trials per ratio from 20 to 24. We also increased controls on the size of the dots, to prevent participants from successfully using dot size, area, or density to guess the correct answer, as detailed below. We also displayed the yellow and blue dot sets on the left and right sides of the screen, respectively, rather than intermingling them, to reduce the likelihood that participants would give the wrong response because they confused the response keys. Additionally, one of the ratio levels—ratios of about 2.5 (e.g., 25 vs. 10, 30 vs. 12)—was large enough that adults should always be able to respond correctly on these trials if they are paying attention: Even 6-month-old infants are able to discriminate numerical magnitudes at ratios of 2 (Xu & Spelke, 2000). Thus, these large-ratio stimuli yielded “catch” trials, which allowed us to estimate individual participants’ lapse rates (i.e., inattention rates), on the basis of their proportions of errors on these trials.

Participants sat at a computer displaying a gray background, on which the experimental stimuli were presented: a set of yellow dots on the left, and a set of blue dots on the right. Both dot sets were contained within a 32 × 18 cm rectangular space in the center of the screen, with a 3-cm gap between the two sets. The participants’ task was to press a key to indicate which set of dots was more numerous, “F” for yellow on the left and “J” for blue on the right. Yellow and blue stickers labeled with the appropriate letters were placed beneath the screen on the left and right to serve as reminders of these instructions.

Each yellow or blue set was composed of 10 to 30 dots. The ratio between the numbers of dots in the paired sets was drawn from one of 13 ratio “bins.” Each bin was a small range of set ratios that allowed for exactly six possible instantiations of the bin’s magnitude within the limits of 10–30 dots per set (see Appendix 3). Thus, the numerical ratio between the two dot sets was not well correlated to the total number of dots presented (r = –.17) or the total area of the dots on the screen (r = –.14). For example, Bin 12 had a mean ratio of 2 (larger/smaller) and possible instantiations of 20 versus 10, 22 versus 11, 24 versus 12, 26 versus 13, 28 versus 14, and 30 versus 15 dots. The mean ratios of the first 12 bins were exponentially spaced between 1.05 and 2, to maximize the task’s ability to detect differences in performance functions within the expected w range. Additionally, the easy “catch” bin with a mean of 2.5 was included to detect lapse rates. In half the trials, the side with more dots also had larger dots and a greater total area than the other side (size congruent). For the other half of the trials, the side with more dots had smaller dots with a smaller total area (size incongruent). Also, there were six possible “average dot sizes,” which limited the range of the diameter of the dots in the more numerous set: 25, 30, 35, 40, 45, and 50 units. Average dot sizes of the less numerous set were adjusted up or down from this to control for size and area congruency, as noted above. Areas of individual dots were allowed to vary randomly by up to 42 % of the average dot area, with the average being maintained across the set. This maximum 42 % area variability corresponds to a maximum 19 % increase in dot diameter. There were two trials per ratio bin, per size, per size congruency. This yielded 24 trials per ratio bin, for a total of 312 trials. Trial order, ratio instantiation used, and which side had more dots were randomly determined by the program, but were based on the same default random seed so that the same set was used for each participant.

Each trial was preceded by a white fixation cross in the center of the screen. Participants then self-initiated each trial by pressing the space bar. The fixation cross then disappeared, and the two sets of dots appeared on the gray background for 200 ms, as is typical of this paradigm (Halberda et al., 2008). The dots then vanished and were replaced by a 200-ms presentation of a single yellow-and-blue snow mask that covered the rectangular area circumscribing the previous locations of the two dot displays. The gray screen then remained empty until the participant responded, at which point the pretrial fixation cross would reappear, awaiting the participant’s command to start the next trial. Each participant completed ten practice trials and then 312 test trials. No feedback was given at any point during testing. Participants could respond immediately after the yellow and blue dots were presented. Reaction times were measured from this time point.

Dot-line task

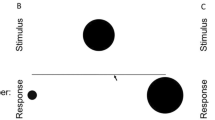
Participants completed a line placement task using nonsymbolic stimuli (sets of dots). In this task, a set of dots flashed on the screen, and participants estimated the placement of its numerical magnitude on a line. For example, if they saw a line anchored by one dot on the left and by three dots on the right, a set of two dots should be placed in the middle. Participants completed two practice trials, with feedback, in which they placed first three and then six dots on a line anchored by one dot on the left and ten dots on the right. After the participants indicated that they understood the task, testing began. Participants were shown a 27.5-cm line anchored by one large dot on the left and 300 small dots on the right (see Fig. 1). The total area of the one large dot was equal to the total area of the 300 small dots. Participants self-initiated each trial by pressing the space bar. After pressing this bar, a fixation cross would appear for 500 ms; it was immediately followed by a 501-ms presentation of a set of dots, and then a 100-ms presentation of a mask composed of unevenly spaced 1- to 3-mm thick black and white diagonal stripes. We note that the speed of the stimulus presentation prevented counting. Thus, participants needed to use their ANS to estimate the numerical magnitudes of the stimuli. Participants then clicked on the line where they thought the dots should go. The line and its anchors remained on the screen throughout each trial.

The dot sets were composed of 20, 40, 60, 80, 100, 120, 150, 180, 200, 220, 240, 260, 280, or 300 dots, for a total of 14 possible nonsymbolic numerical magnitudes. The continuous extent of the dot sets was controlled in two different ways. On half of the trials, the total area was allowed to vary, increasing with the number of dots shown, but the average size of each dot was held constant, equal to the average size of the dots in the 300-dot anchor (area varied, dots constant: AVDC). On the other half of the trials, the total area of the dots was held constant, equal to the total area of the 300-dot anchor, but the size of the dots varied, decreasing as set size increased (area constant, dots varied: ACDV). Thus, continuous extent did not consistently vary with numerical magnitude. Participants completed one trial per nonsymbolic numerical magnitude per continuous-extent control types, for a total of 28 trials. No feedback was given during testing. The small number of trials combined with this lack of feedback limited the possibility that participants could learn which continuous-extent strategy was viable for placing the stimuli. Moreover, the lack of feedback meant that assessing whether a continuous extent strategy could be used successfully to place a particular dot set would require that the participant assess the numerical magnitude of the set. Thus, participants had to base their responses on the perceived numerical magnitude of a set if they were to be successful. Trials were presented in random order. This task was typically completed in 2–5 min.

Dot-ratio task

The dot-ratio task was similar to the dot-line task, except that participants were asked to give an explicit symbolic ratio rather than to place dots on a line. We constructed 28 nonsymbolic ratios with the 28 dot stimuli described for the dot-line task, displayed in a fractional relationship to a 300-dot denominator (see Fig. 2). Participants initiated each trial by pressing the space bar. After they pressed this bar, a fixation cross appeared for 500 ms and was immediately followed by a 501-ms presentation of a dot ratio, then a 100-ms presentation of a striped mask, like that described above. Participants then needed to type in the ratio they saw (e.g., 1/3). The 28 trials were presented in random order, one trial for each possible nonsymbolic ratio stimulus. Prior to testing, to ensure understanding of the task, feedback was given on two practice trials for which participants were to give ratios for three versus ten dots and six versus ten dots. No feedback was given during testing. This task was typically completed in 2–5 min.

Dot-number task

The dot-number task was similar to the dot-line and dot-ratio tasks, except that participants were asked to provide an explicit symbolic estimate of the number of dots in each set. The stimuli were the same 28 dot stimuli described for the dot-line task. Participants initiated each trial by pressing the space bar. After pressing this bar, a fixation cross appeared for 500 ms, which was immediately followed by a 501-ms presentation of a dot set, then a 100-ms presentation of a striped mask. Participants then typed in the number of dots that they saw (e.g., 100). The 28 trials were presented in random order, one trial for each dot set. Prior to testing, to ensure understanding of the task, feedback was given on two practice trials in which participants were to estimate three and six dots. No feedback was given during testing. This task was typically completed in 2–5 min.

SMAP task

Participants completed a SMAP task in which they placed the symbolic numbers 0, 20, 40, 60, 80, 100, 120, 150, 180, 200, 220, 240, 260, 280, and 300 on a 27.5-cm line anchored by the symbolic numbers 0 and 300. Participants initiated each trial by pressing the space bar, which caused a digit to appear above the center of the line, where it remained until a response was given via a mouse-click on the line. A total of 15 trials, one for each value, were presented in random order. No feedback was given during testing. However, to ensure understanding of the task, feedback was given on two practice trials in which participants placed the numbers 33 and 14 on a line anchored by 0 and 100. This task was typically completed in 1–3 min.

Results

Among the 247 participants, six (2 %) did not complete all of the tasks due to early withdrawal or equipment failure: One did not complete the three dot-estimation tasks or the SMAP task, three did not complete the dot-discrimination task, and two completed none of these tasks. An additional 22 participants (9 %) were found to be noncompliant on the dot-discrimination task and/or the SMAP task. We described how we identified noncompliant participants in detail below. To better allow for comparisons of the effects, the analyses in the text below refer to the subset of 219 participants (89 %; 128 male, 91 female, mean age = 18.9) who completed and were compliant on all tasks, unless otherwise noted. However, we also conducted parallel analyses that included data from all of the participants who were compliant on the tasks relevant to the analysis in question, with similar results. These data are available from the first author.

Data coding

Dot-discrimination task

We used a maximum likelihood model described by Halberda and Feigenson (2008) to estimate the ws for each participant (see Appendix 4). Estimates were found (a) using the full data set, (b) separately for the subsets of size-congruent trials and size-incongruent trials, and (c) separately for subsets found via a random split including half of the trials in each bin for each size congruency type (the same split was used for each participant). We estimated these ws for each participant in two ways: assuming a lapse rate of 0 (w ₀) and using an estimated lapse rate for each participant (w _L). Lapse rates were estimated from the participants’ error rates on the “catch” trials, the trials with ratios between 2.4 and 2.6. As we discussed above, adults should always get these trials correct if they were paying attention. Thus, all errors on these trials could be attributed to random answering resulting from a lapse in attention. Because inattentive participants should choose by chance the correct answer on half of these randomly answered lapsed trials, we estimated each participant’s lapse rate as two times the proportion of incorrect trials. Catch trials were only used once in the w _L calculation—to estimate the lapse rate—and not used again with the rest of the trials in the subsequent maximum likelihood calculation that corrected for that estimated lapse rate. Otherwise, all data points were included in the analyses.

Dot-line, dot-number, dot-ratio, and SMAP tasks

Responses on the dot-line and SMAP trials were converted to the numerical value referenced by that position on the line. No responses were missing or uncodeable. Responses to the dot-number and dot-ratio tasks were converted to decimal numbers (e.g., “four” → 4; “1/4” → .25). For these two tasks, 0.4 % of responses were missing or uncodeable (e.g., “e30”). Task performance was scored on the basis of the codeable responses. We calculated the R ² of the fit of the responses to a linear function and the mean absolute distance of the responses from the correct value (ADC) for each participant on each of the dot-estimation tasks (dot-line, dot-number, and dot-ratio), for each of the two subsets of area controlled trials (the subset of trials in which the total area varied with the number of dots and dot size was constant [AVDC] and the subset of trials in which the total area was held constant and dot size varied [ACDV]). For each task, the R ² for the two subsets were averaged to yield each participant’s mean R ². The same was done for the ADCs. We also found the R ² and ADC of the responses to the 14 SMAP trials with stimulus values ranging from 20 to 300. The trials in which the stimulus was 0 were excluded, so that the stimulus values analyzed would match those of the dot-estimation tasks.

Identifying noncompliant participants

Dot-discrimination task

We identified 19 participants (8 %) with lapse rates of 0.5 or greater to be noncompliant. A lapse rate over 0.5 would indicate that the participant was inattentive and answered randomly on more than half the trials. We also identified as noncompliant participants whose w estimates were greater than or equal to 1.0, either overall or for any of the tested halves (18 participants, 7 %). The results from prior research (Halberda et al., 2008) estimating w using a similar task placed ws equal to 1.0 at more than seven standard deviations above the mean. A w of 1.0 would indicate that a person cannot differentiate magnitudes at a ratio less than 2:1. Recall that 12-month olds can discriminate magnitudes at 3:2 ratios (w ≤ 0.5; see Cantrell & Smith, 2013, for a review). Thus, w estimates of 1.0 or greater indicated either an abnormal ANS or, more likely among our college student participants, sufficiently high lapse rates to constitute noncompliance with the task. A great deal of overlap existed in the participants identified by these exclusion criteria. Of the 18 participants excluded due to overly high w estimates, 16 also had lapse rates greater than 0.5, with the remaining two participants being near the cutoff, with lapse rates of 0.5 and 0.42. Thus, converging evidence exists that both of these methods—and our catch trials, in particular—were successful at identifying noncompliant participants. On the basis of these criteria, 21 participants of the 242 who completed this task (9 %) were found to be noncompliant.

Estimation tasks

Although estimation tasks similar to those used here have been used in prior studies, these particular versions of the estimation tasks are novel. As such, no data are available in the literature as to what constitutes “normal” adult performance. To best parallel the procedure used to detect noncompliant participants on the dot-discrimination task, we decided to exclude participants whose R ²s were seven standard deviations away from the mean based on the data from all 244 participants who completed these tasks. Performance was sufficiently variable on the dot-line, dot-number, and dot-ratio tasks that R ²s would have needed to be outside the possible range to be seven standard deviations from the mean. As such, no participants were identified as being noncompliant on these tasks. Performance on the SMAP task was less variable (N = 244, M = .951, SD = .094), and R ²s less than .29 were more than seven standard deviations below the mean. This cutoff point identified two participants as noncompliant on the SMAP task, one of whom was also identified as noncompliant on the dot-discrimination task. These participants were excluded from the final sample. Of interest, in a personal communication, John Opfer (May 8th, 2015) suggested that noncompliance can be established on symbolic number-line tasks like our SMAP task simply by excluding participants who do not show a statistically significant correlation between the stimulus value and their response. According to this criterion, R ²s below .28 on the SMAP task would indicate noncompliance, and the same two participants would be identified. Thus, converging evidence exists that a cutoff of seven standard deviations does indeed detect noncompliance on the SMAP task.

Final sample

The final sample size was 219 after excluding noncompliant participants. The mean estimated lapse rate was higher (lapse rate = 0.15, SD = 0.25, range = 0 to 1.25) among the 242 participants who completed this task, including those found to be noncompliant, than for the final sample of 219 (lapse rate = 0.08, SD = 0.12, range = 0 to 0.5). Excluded participants also had significantly poorer scores on objective numeracy and subjective numeracy than did those in the final sample [ONS means: 3.36 (SD = 1.57) and 4.42 (SD = 1.60) among the excluded and final participants, respectively, t(245) = 3.33, p = .001, Cohen’s d = 0.67; SNS means: 4.15 (SD = 0.94) and 4.49 (SD = 0.84) among the excluded and final participants, respectively, t(245) = 2.01, p = .046, Cohen’s d = 0.40].

Performance and reliability

Objective numeracy and subjective numeracy tasks

The mean score on the seven question ONS task was 4.42 (SD = 1.60) and on the SNS task was 4.49 (SD = 0.84).

Dot-discrimination task

Mean w estimates and their correlations are presented in Table 1. With a mean of 0.22 (SD = 0.06), our estimates of w _L are consistent with past estimates of adult ANS Weber fractions (Cordes et al., 2001; Inglis & Gilmore, 2014; Lindskog et al., 2013; Price et al., 2012; Whalen et al., 1999). We found large correlations between the w ₀ estimates from commensurate halves for the different size-congruency conditions (r = .79) and for the random split (r = .81), indicating that this task had good reliability. This was partially driven by the lapse rate rather than by the underlying w. The correlation between the overall w ₀ and lapse rate was quite high (r = .80, p < .001) and was greater than .71 for all four of the w ₀ estimates for the various halves, indicating that the w ₀ estimates of ANS acuity may have been biased by the lapse rates. Nevertheless, the w estimates calculated on the basis of the individual lapse rate estimates (w _L) still showed large correlations (r > .57) between commensurate halves, with reliability greater than .73. [Note: We report reliability here in terms of the Spearman–Brown coefficient, 2r/(1 + r), because it yields a score similar to Cronbach’s alpha, but is less susceptible to bias when assessing two variables, such as with split-half reliability; Eisinga, Grontenhuis, & Pelzer, 2012.] Thus, performance on this task was reliable, and the w estimates obtained from it were reliable, even after accounting for the lapse rate.

Table 1 Study 1: performance on the dot-discrimination task (N = 219)

Full size table

Dot-estimation tasks

The mean R ²s and ADCs for the three dot-estimation tasks and the SMAP task, as well as the correlations among them, are presented in Tables 2 and 3. Participants typically showed linear, but imprecise, performance on all three dot-estimation tasks, with mean R ²s near .7. Such performance is consistent with the use of the ANS to assess magnitudes and determine responses, with additional noise in the responses potentially due to the task demands, possibly including the use of symbolic numbers for estimates in the dot-number and dot-ratio tasks. Of the three dot-estimation tasks, only the dot-line task yielded consistently reliable performance (Spearman–Brown ≥ .6). Adequate (Spearman–Brown ≥ .6) to excellent (Spearman–Brown ≥ .9) reliability was found when we correlated the ADC and R ² values between the two subsets of the dot-line task, and when we correlated the task’s mean R ²s and mean ADCs. Performance was not as consistent for the dot-number or dot-ratio tasks. This pattern seems likely due to the bounded nature of the dot-line task, which helps ensure that participant responses are all on the same scale and limits the degree to which participants can provide answers that are extreme outliers. The scaling issue is particularly relevant to the dot-number task, since it has been found previously that people systematically underestimate the cardinal value of dot sets (see Taves, 1941). Thus, a person with extremely precise dot-number task responses (R ² = .95) that were consistently underestimated by 50 % could have a much poorer ADC score than a person whose answers were much less precise (R ² = .7) but were unbiased. By comparison, outliers are particularly problematic in the dot-ratio task. For example, nine participants in the final sample gave responses greater than 3.0 on the dot-ratio task, despite all of the stimulus ratios being less than or equal to 1. When these participants were dropped from consideration, the correlation between the dot-ratio task’s R ² and ADC values increased considerably, from –.33 to –.83, (p < .001, Spearman–Brown = .91), as did the correlation between the ADCs found for the area-correlated and area-constant trials, increasing from –.01 to .27 (p < .001, Spearman–Brown = .42), whereas the correlation between the R ²s of the two different kinds of trials remained stable (.42 vs. .44). Thus, removing outliers from consideration can improve the reliability of the dot-ratio task, but the dot-line task was reliable without such cleaning. Analyses of the R ²s of the logarithmic fit yielded results similar to those of the linear fit and are available from the first author.

Table 2 Study 1: mean linear fits and mean absolute distance from correct (ADC) for performance on the four estimation tasks (N = 219)

Full size table

Table 3 Study 1: correlations between estimation and discrimination tasks (N = 219)

Full size table

SMAP task

The SMAP task included a single trial for each of the 14 stimulus values. Thus, to judge its internal reliability, we split the task using every other value. Subset 1 included the trials with the symbolic numbers 20, 60, 100, 150, 200, 240, and 280 as stimuli, whereas Subset 2 included the trials with the symbolic numbers 40, 80, 120, 180, 220, 260, and 300 as stimuli. Participants were typically both linear and extremely precise on the task: Considering all trials, the mean R ² was .96 (SD = .05). This performance is not consistent with the use of analog magnitudes alone to assess stimulus values and determine responses: Responses were too accurate for values to have been placed solely using the relative analog magnitudes mapped to stimulus values and anchors, given that these analog magnitudes have ANS-like acuity (see Dehaene et al., 1993; Dehaene & Cohen, 1998). Simulations of 10,000 participants with w ranges like those determined from the dot-discrimination task (M = 0.22, SD = 0.06) indicated that one should expect a mean R ² of .78 (SD = .14), if the variability in analog numerical magnitude representations was the only source of error, with no added noise from task demands. This analysis indicates that our participants likely used other strategies, such as line bisection, in addition to or instead of analog magnitude comparisons to place the values on the line. As we suggested earlier, this potential confound may compromise this task’s validity as an assessment of ANS acuity. The split-half reliability on this task was mixed, with small-to-medium correlations between the subsets’ R ² s (r = .31, p < .001, Spearman–Brown = .47) and large correlations between the subsets’ ADCs (r = .58, p < .001, Spearman–Brown = .73). Additionally, the overall R ²s and ADCs found for the 14 trials with stimulus values greater than 0 showed a large correlation to each other (r = –.79, p < .001, Spearman–Brown = .89).

Correlations between discrimination and estimation tasks

As is illustrated in Table 3, the mean R ²s of all dot-estimation and SMAP tasks are correlated with each other and with the dot-discrimination task’s w ₀ estimates (based on a zero lapse rate). Interestingly, they are also all correlated with the w _L estimates (based on individual lapse rate estimates), and to the estimated lapse rate, despite the fact that w _L and lapse rate are not correlated with each other. This pattern suggests that performance on all of the tasks was confounded to some extent with individual differences in effort or attention, and that these lapse rates from the dot-discrimination task may, at least in part, account for these differences. Performance on the dot-line task was the best overall predictor of the estimation measures and was significantly correlated with the dot-discrimination task’s w _L (mean r = .30; see Tables 3 and 5). However, after the nine dot-ratio outlier participants were dropped from consideration, the correlations of the dot-ratio task to the other metrics became similar to those of the dot-line task, with significant small- to medium-sized correlations with all the other measures, excepting only the dot-number ADC. The absolute values of these rs ranged from .18 (dot-ratio ADC and lapse rate) to .39 (dot-ratio R ² and dot-line R ²). The correlations of the SMAP task to the other potential measures was similar to that of the dot-line task, although SMAP’s correlation to w _L was somewhat smaller (mean r = .21) than the dot-line task’s (mean r = .30).

Correlations between performance on general numeracy measures and discrimination and estimation tasks

The correlations of the discrimination and estimation tasks to the SNS and ONS are presented in Table 4. As can be seen, better performance on all of the other tasks was correlated with higher ONS scores (average absolute rs ranging from .12 to .38; see Table 5). Better ONS was also associated with lower lapse rates on the dot-discrimination task (i.e., with greater attention, r = –.14). SNS was similarly correlated with the various measures (average absolute rs ranging from .11 to .27; see Table 5), although it was not significantly correlated to lapse rates (r = –.08). These results could mean that ONS relates only to possible confounding effects of effort on task performance, rather than to underlying ANS acuity. However, correlations of ONS and SNS to the dot-discrimination task’s w estimates changed only slightly after accounting for the lapse rate. Furthermore, regressing both lapse rate and w _L on ONS, we found that both factors predicted ONS independently (lapse rate: β = –.15, t = –2.3, p = .022; w _L: β = –.26, t = –4.0, p < .001).

Table 4 Study 1: correlations between estimation and discrimination tasks to numeracy assessments (N = 219)

Full size table

Table 5 Study 1: overview of the reliability and intertask correlations of the discrimination and estimation tasks (N = 219)

Full size table

Math SAT scores were obtained from 65 of the 219 participants (30 %). Despite this low power, a significant, medium-sized correlation existed between Math SAT scores and w _L (w estimates accounting for lapse rates; r = –.36, p = .003). However, for w ₀ estimates (estimates that did not account for lapse rates), the correlation to Math SAT was neither significant nor in the predicted direction (r = .11, p = .37). The only other potential acuity measure that had a significant correlation with Math SAT scores was the dot-ratio task (R ²: r = .26, p = .03; ADC: r = –.32, p = .01).

Discussion

The goal of Study 1 was to test the reliability of several potential metrics of ANS acuity: a dot-discrimination task, three tasks in which participants estimated nonsymbolic numerical magnitudes, and a symbolic number-mapping task. Performance on the tasks correlated with each other and showed similar patterns of correlation to the objective and subjective numeracy measures (see Tables 3, 4, and 5). This convergence indicates that the tasks tap into the same cognitive construct(s), and thus may reflect individual differences in ANS acuity to greater and lesser extents.

The present results replicated past findings that general mathematical ability and ANS acuity are associated (Halberda et al., 2008; see Chen & Li, 2014, for a review). Moreover, we found correlations of ONS and SNS with the dot-discrimination task’s w estimates that persisted even after accounting for participants’ inattention to the task via the lapse rate estimates. This finding further supports the conclusion that correlations between acuity measures and general numeric ability measures reflect, at least in part, a connection to underlying ANS acuity, rather than to other factors that may be captured in such tasks, such as effort or sustained attention.

Of the four dot tasks, the dot-discrimination task and dot-line task were more reliable than the dot-number and dot-ratio tasks. Both the dot-discrimination task and the dot-line task achieved good internal reliability without the need to drop outlier trials (average split-half reliabilities > .7; see Table 5). In contrast, the dot-number task showed poor reliability (average split-half reliability = .53; see Table 5), and reliability on the dot-ratio task was unacceptably low (average split-half reliability = .30; see Table 5). It should be noted that, although the stimuli were nonsymbolic on all four of these tasks, the responses were symbolic on two of the tasks. In particular, the dot-number and dot-ratio tasks required participants to respond with symbolic Arabic numbers. Symbolic number understanding, thus, may have affected performance on these tasks, reducing the reliability of their ANS acuity estimates. Additionally, the symbolic ONS and SNS measures correlated more strongly with the most reliable of the estimation tasks (the dot-line task) than they did with the dot-discrimination task.

The SMAP task showed the same pattern of correlations as did the dot-estimation tasks, despite its use of symbolic stimuli. It showed better overall split-half reliability than did the dot-number and dot-ratio tasks, though not as good as that of the dot-line task. Moreover, it was more strongly correlated to the dot-discrimination task’s w _L than were the dot-number or dot-ratio tasks, although again not as strongly as the dot-line task. Thus, SMAP scores reflect ANS acuity to some extent. However, given the present finding that SMAP performance was better than could be achieved solely using analog magnitudes with ANS-like acuity, combined with prior evidence that participants used non-ANS-based strategies to bolster their accuracy (Barth & Paladino, 2011), the reasons for the connection between SMAP performance and ANS acuity remain unclear. It could be that the extent of the use of analog magnitudes is sufficient to yield correlations between ANS acuity and SMAP performance, despite the possible involvement of other properties and processes, such as the accuracy of the mapping between symbolic numbers and numerical magnitudes and line bisection strategies. Alternatively, it may be that analog magnitudes are not invoked during the SMAP task, but that ANS acuity and SMAP are correlated because both are correlated with overall numeric ability: Indeed, controlling for ONS, the partial correlation of w _L and SMAP’s ADC was only .19 (p = .005), and the partial correlation of w _L and SMAP’s R ² was both not significant and not in the predicted direction (r = .06, p = .356). It is also possible that the correlation is due to both ANS acuity and placement strategies (such as line bisection) drawing on the same underlying cognitive ability (such as the ability to perceive relative proportions; Matthews & Chesney, 2015). Additional research will be needed to understand the role of the ANS as compared to other processes when using symbolic stimuli, symbolic estimates, and line placements.

Of the tasks tested here, the dot-discrimination task appeared to provide the most reliable assessment of individuals’ ws. It had the most consistently high split-half reliability of the potential ANS measures tested, and it was predictive of better, more linear performance in the other estimation tasks. This reliability and predictive power was maintained even after accounting for lapse rate. Moreover, it was the only task of those tested able to separately assess aspects of effort and acuity that appear to influence estimation performance. Estimated lapse rates and w _L (estimates of w that took lapse rates into account) were not significantly correlated with each other, yet they both were correlated to performance on the estimation tasks. Both larger lapse rates and larger w _Ls predicted worse estimation performance, suggesting roles for both ANS acuity and effort in the estimation tasks. This ability to simultaneously assess ANS acuity and task attention may yield wider benefits to researchers than would an assessment of ANS acuity alone, since it can serve as a measure of individual differences in effort on the day of testing. This may prove to be an important predictor for many tasks. Indeed, although lapse rate is deliberately not a measure of ANS acuity, it is, in fact, predictive of performance on the other ANS acuity measures and on the ONS. Moreover, excluded participants not only had poorer lapse rates, but also poorer ONS and SNS scores, than those in the final sample. It appears that both ONS scores and performance on ANS tasks (without accounting for lapse rates) partially reflected participants’ effort on the day of testing.

Since the dot-discrimination task can be completed in 5–10 min and can be instantiated easily using the readily available Panamath (2013) software, it offers a viable option for researchers wanting to quickly assess individual differences in ANS acuity. Among the estimation tasks, the dot-line task showed the most promise. It was the only one of the three dot-estimation tasks to show good (Spearman–Brown ≥ .7) mean internal reliability and had small- to medium-sized correlations with performance on the other estimation tasks, the discrimination task, and the general numeracy assessments (see Table 5). Although this task cannot be used to calculate w estimates, it does require the use of ANS estimation, and it shows the benefits of a bounded task in that it limits outlier issues so as to enhance reliability. Moreover, it typically took only 2–5 min to complete, making it quite practical to implement. The SMAP task also showed adequate overall reliability (Spearman–Brown ≥ .6) and association with ANS acuity in a 1- to 3-min task. Moreover, it required no animation, and thus can be conducted using paper and pencil. We continue our evaluations of these tasks in Study 2.

Study 2

Study 1 addressed reliability within a single session. Although ANS acuity is thought to be a stable cognitive trait, performance at a single time point nonetheless may be influenced by a variety of external factors, such as the participant’s motivation or mood on a given day, how much sleep she or he had the night before, and so forth. Therefore, we conducted Study 2 to examine test–retest reliability after a one-week delay. We looked specifically at the dot-discrimination, dot-line, and SMAP tasks, the measures showing the greatest internal reliability in Study 1. We also included the SNS task and a longer version of the ONS task at both time points. Test–retest correlations should be large for the measure to be a useful indicator of a stable cognitive trait (r > .5, Spearman–Brown > .66). Thus, a much smaller sample was needed for Study 2. A power analysis indicated that a final sample size of 29 was necessary to achieve an 80 % likelihood of successfully detecting such large correlations.