On the replication of Kristofferson’s (1980) quantal timing for duration discrimination: some learning but no quanta and not much of a Weber constant

Abstract

This study revisited Kristofferson’s (Perception & Psychophysics 27:300–306, 1980) report showing that, with sufficient practice at interval discrimination, the relationship between timing variability and physical time is a step function—in other words, that psychological time is quantized. Two participants completed 260 sessions of a temporal discrimination task, 20 consecutive sessions for each of 13 base durations ranging from 100 to 1,480 ms. The data do not replicate Kristofferson’s (Perception & Psychophysics 27:300–306, 1980) quantal finding, and it is argued that the effect Kristofferson reported may have been due to specific methodological decisions. Importantly, the data show (1) some limitation of Weber’s law for time, even for the narrow range of the present investigation, and (2) that extensive training provides some modest benefit to temporal discrimination, mainly for longer intervals, and that this benefit primarily occurs in the first few sessions.

Do changes in sensation occur in discrete steps or along a continuum? Given the quantization of many physical entities and the all-or-nothing nature of some neural processes, the question is worth addressing (e.g., VanRullen & Koch, 2003). However, establishing steps in sensation is a very difficult research avenue and, probably consequently, a somewhat neglected one. Some 30 years ago, however, Kristofferson (1980) made a noteworthy attempt to demonstrate that the psychological experience of time is quantized. The present work follows on from this attempt.

A fundamental question in the field of time perception concerns the functional relationship between the variability of internal representations and the magnitude of the intervals one is dealing with (Bangert, Reuter-Lorenz, & Seidler, 2011; Grondin, in press; Killeen & Weiss, 1987). Many time perception models assume that variability increases linearly with physical time, in keeping with Weber’s law. This feature is referred to in many contemporary models as the scalar property (Gibbon, 1977; Gibbon & Church, 1984).

By contrast, Kristofferson (1967, 1976, 1977, 1980) argued for a “time quantum,” a basic unit of temporal variability labeled q. Kristofferson postulated that variation in the representation of a given duration follows a triangular distribution with base 2q. This assumption was originally motivated by the idea that perceptual onset and offset latencies are each independently and uniformly distributed over a range of q milliseconds (Allan, Kristofferson, & Wiens, 1971), but in later work the emphasis on afferent latencies was abandoned (e.g., Kristofferson, 1977). Crucially, the value of q is taken to be constant for a range of durations, meaning that the ability to discriminate two temporal intervals will depend only on the difference between them, not on their absolute magnitudes. One interpretation of q is that it corresponds to the time between events generated by an internal clock, which dictate when attention can switch from one channel to another and when information can pass from one stage of processing to the next (e.g., Allan et al., 1971; Allan & Kristofferson, 1974b; Kristofferson, 1967). This idea is similar to the perceptual moment hypothesis (e.g., Stroud, 1955), which posits that the psychological time scale is partitioned into discrete intervals such that sensory events can be temporally ordered only if they fall into separate intervals. Ulrich (1987) provides a helpful exposition of the attention-switching and perceptual moment hypotheses in the context of temporal order judgments.

The prediction that q, the unit of temporal variance, remains constant across a range of durations has found some support (e.g., Allan & Kristofferson, 1974a; Allan et al., 1971). The most compelling data come from Kristofferson (1980). Kristofferson (1980) argued that extensive training is required to produce stationary discrimination performance and that, because practice effects are duration specific, discrimination at a given base duration should be thoroughly practiced before moving on to the next duration. Accordingly, Kristofferson undertook a program of 20 consecutive 300-trial sessions for each of 13 base durations (100–1,480 ms). The results are striking. For sessions 1–5, Weber’s law holds; for sessions 18–20, it does not. Specifically, for the last 3 sessions, the relationship follows a step function: For certain ranges of durations, q is approximately constant. What is more, the quantum size doubles from one step to the next, taking values of 13, 25, 50, and 100 ms. To account for this doubling, Kristofferson suggested that timing involves counting units of size q, where an upper limit to the counter means that q is doubled whenever the to-be-timed interval necessitates more counts than can be accommodated. (The details of this proposal are somewhat vague, and it is not clear whether it is conceptually coherent.)

Kristofferson’s (1980) demonstration of a step function in q has profound implications for the neural basis of timing. However, as Allan (1998) noted, “These data are based on one subject, the author (Kristofferson), who served in hundreds of sessions. Although the data are widely cited, they have not been replicated.” (p. 103). The present article attempts such a replication. More generally, it investigates the relationship between physical duration and the variability of internal timing, and the effects of learning on temporal discrimination.

About Weber’s law for time

Kristofferson (1980) succinctly reviewed the literature on Weber’s law for time, relying mainly on one empirical report—that of Getty (1975), who concluded that some form of Weber’s law applies to time for intervals briefer than 2 s. In the past 30 years, convergence of human and animal timing research has been driven by the acceptance of the scalar property for a large range of durations. The scalar property means that the standard deviations of time estimates rise linearly with their mean, producing a constant Weber fraction (Gibbon, 1977). This property is central to scalar expectancy theory (SET), which was developed to account for animal timing (Gibbon & Church, 1984; Zarco, Merchant, Prado, & Mendez, 2009) and generalized to human timing (see Wearden, 2003). According to SET, time estimations are based on the output of an internal, central clock. The clock is described as a pacemaker-counter device, with the pacemaker emitting pulses and their accumulation forming the basis of the experience of time. This pacemaker-counter mechanism is under the control of attention. If attention is shared between a time task and a nontemporal task, fewer pulses are accumulated, and the psychological experience of time is changed (see, e.g., Casini, Macar, & Grondin, 1992; Grondin & Macar, 1992; Macar, Grondin, & Casini, 1994). Indeed, errors in time estimation could be caused by the properties of the clock (Rammsayer & Ulrich, 2001; see Grondin, 2001, 2010a), by some failure of the counter (Killeen & Taylor, 2000), by changes in the latency to begin/end the accumulation of pulses (e.g., Matthews, 2011a), or by the involvement of attention (Gamache, Grondin, & Zakay, 2011; Grondin & Rammsayer, 2003). Moreover, errors could be caused by memory processes (e.g., Gamache & Grondin, 2010; Grondin, 2005) or decisional processes, as reported by Allan and Kristofferson (1974b) and recognized in the information-processing version of SET (Gibbon & Church, 1984; Gibbon, Church, & Meck, 1984). In short, SET is a widespread and flexible model of human timing that predicts a constant Weber fraction.

While the scalar property for time has been implicitly accepted by many researchers, other data challenge this assumption. Indeed, there was already in Getty’s (1975) data some evidence that the Weber fraction gets higher when the intervals to be discriminated are longer than 2 s. In fact, there is reason to believe that 1.5 s, rather than 2 s, marks a critical transition (Gibbon, Malapani, Dale, & Gallistel, 1997), and some portions of the animal timing literature indicate that there is a maximum local sensitivity at 1.2 s (Crystal, 2006). Moreover, there is evidence in the human timing literature that the Weber fraction is higher at 2 s than at 0.2 s (Lavoie & Grondin, 2004), that it is higher at 1 s than at 0.2 s (Grondin, 2010b), and that it is higher at 1.9 s than at 1 s (Grondin, in press). There is also evidence that 1.2 or 1.3 s represents a critical breakpoint for processing time (Bangert et al., 2011; Grondin, Meilleur-Wells, & Lachance, 1999). Allan (1979) and Woodrow (1951) reviewed older research that similarly argues against Weber’s law for time.

In short, there are reasons to dispute the notion that there is a linear relationship between the difference threshold and the magnitude of the time interval. One possibility is that there is a step relationship like the one reported by Kristofferson (1980), at least for intervals briefer than about 1.5 s.

Learning time

A critical issue embedded within Kristofferson’s (1980) approach concerns the benefits that might be gained by extensive training. Indeed, Kristofferson emphasized that training reduces noise which would otherwise mask the quantal nature of psychological time. However, he made no systematic report of the benefit over sessions at each standard duration but reported only a general analysis where all base durations were grouped.

Since the publication of Kristofferson’s (1980) work, other studies have examined the effects of extensive training on temporal discrimination, with mixed results. One thorough investigation was provided by Rammsayer (1994). Participants completed 20 sessions of auditory interval discrimination, with a standard interval of 50 ms. The experiment showed that there was no training effect (no improvement of the discrimination threshold) when the first 5 sessions (conducted within the same week) were compared or when the four groups of 5 sessions were compared. This nonsignificant result was obtained whether the intervals to be discriminated were filled or empty (two separate experiments). Another experiment involving visual intervals lasting about 250 ms also showed no benefit over five 300-trial sessions (Grondin, Bisson, Gagnon, Gamache, & Matteau, 2009). By contrast, Wright, Buonomano, Manhcke, and Merzenich (1997) and Karmarkar and Buonomano (2003) found substantial improvement in auditory temporal discrimination over the course of several days’ training, and similar learning has been reported for vision (Westheimer, 1999) and somatosensation (Nagarajan, Blake, Wright, Byl, & Merzenich, 1998). The performance improvement is typically substantial at first but slows after a few sessions, consistent with a power law (e.g., Bartolo & Merchant, 2009). Learning is also typically most pronounced for participants whose initial performance is poor (Nagajaran et al., 1998). Differences in prior experience and ability may, therefore, underlie the difference between studies which find learning and those which do not, as may differences in the number, length, and spacing of the training sessions.

Even when learning does occur, it is not clear precisely what is learned. Wright et al. (1997) and Karmarkar and Buonomano (2003) reported that learning about a 100-ms interval demarcated by 1-kHz tones generalized to tones of a different frequency but not to intervals of a different length, suggesting that training selectively improves the representation of a particular duration. However, other work has found some generalization to nearby durations (e.g., Bartolo & Merchant, 2009; Nagajaran et al., 1998). Similarly, although some studies have reported cross-modality transfer of learning (e.g., Bartolo & Merchant, 2009; Nagarajan et al., 1998), others have found no such effect (Grondin, Gamache, Tobin, Bisson, & Hawke, 2008; Grondin & Ulrich, 2011; Lapid, Ulrich, & Rammsayer, 2009). In short, both the nature of the representations underlying temporal discrimination and the effects of prolonged practice on such representations are currently unclear.

The primary goal of the present study is to replicate Kristofferson’s (1980) data. His results provide the most compelling evidence for the quantal nature of psychological time, and replication is a starting point for more thorough investigation. Irrespective of whether the present experiment replicates Kristofferson’s step function, the study (1) provides a test of the trainability of interval discrimination in the auditory modality for different durations, (2) provides an opportunity to examine the functional relationship between the variability of time representations and time magnitudes up to about 1.5 s, and (3) allows us to see if and how this relationship changes as a function of training.

Method

Participants

Two participants completed the 260 experimental sessions of the experiment. One (W.M.) was the first author, and the other (F.M.S.) was a 20-year old student at Laval University who received $1,000 for her participation. Note that while Kristofferson already had extensive experience in duration discrimination before performing this task (Kristofferson 1976, 1977), the present participants had only moderate experience with this type of task.

Stimuli, design, and procedure

All aspects of the stimuli, design, and procedure were closely modeled on Kristofferson (1980). Sets of six stimuli were prepared, one set for each of 13 base durations ranging from 100 to 1,480 ms. The stimuli were pairs of auditory pulses demarcating empty intervals; the pulses were 2000-Hz sinusoids lasting 10 ms, inclusive of 2.5-ms cosine ramps at onset and offset, presented in quiet testing rooms. (W.M. used Sennheiser CX300II in-ear headphones; F.M.S. used the speaker of a portable computer.) The onset-to-onset times of the pulses defined durations labeled D ₁ to D ₆. The durations were arranged symmetrically around each base duration and are listed in Table 1. In each set, D ₁ and D ₄ are widely spaced around the base duration; Kristofferson intended them to be perfectly discriminable and to serve as “monitoring” stimuli for estimating the probability that a stimulus is processed. By contrast, D ₂ and D ₃ are closer to the base duration and are intended to be imperfectly discriminable, and D ₅ and D ₆ are very close together, making discrimination very difficult.

Table 1 Stimulus durations for each base duration, the differences between selected pairs of durations, and the order of measurement used by Kristofferson (1980)

For each of the 13 base durations, the participants completed 20 sessions of 300 trials, divided into three blocks of 100, with a brief rest in between blocks. On each trial, one stimulus was presented and the participant had to classify it as “short” or “long,” depending on whether it was shorter or longer than the base duration. For sessions 1–15, the stimulus durations were drawn from D ₁, D ₂, D ₃, and D ₄. Each duration was presented equally often within each block, in random order. For sessions 16–20, durations D ₅ and D ₆ were substituted in place of D ₁ and D ₄. That is, the two monitoring stimuli were replaced with durations that were hard to discriminate.

The 20 sessions at each base duration were run consecutively, 2 per day, with at least 2 h between sessions and at least 2 days between the end of testing at one base duration and the start of the next.¹ Each trial started with a 1-s blank interval, followed by presentation of the stimulus and then a blank interval until the participant responded by a buttonpress, after which visual feedback indicating whether the duration was “short” or “long” was presented for 500 ms.

For participant F.M.S., the order of the base durations was the same as for Kristofferson (1980; see Table 1); for W.M., the reverse ordering was used.² Minor aspects of this procedure differed from that of Kristofferson. For him, there was only one session per day, the four stimuli in a given block were presented only an “approximately” equal number of times, and each trial began with an auditory warning signal of unspecified duration (Kristofferson also does not state the duration of his visual feedback). These modifications were judged unlikely to be crucial to the results.

Results

The data analyses were conducted in two steps. The first used the approach taken by Kristofferson (1980); the second used a more common approach to the psychometric function, which also served as the basis for an analysis of learning.

Kristofferson’s analysis

We began by applying the approach taken by Kristofferson (1980). For the purposes of exposition and comparison, we include a re-presentation of his data before describing our own results.

Kristofferson’s (1980) analysis is based on a framework similar to conventional signal detection theory, but where the variability in the internal representation of time is described by an isosceles triangle rather than a Gaussian curve. The triangle has base 2q, where q is referred to as the time quantum, as described above. The observer has a response criterion D _c , and the probability of responding “long” to a given stimulus duration is given by the area of the triangle to the right of this criterion. Given the response probabilities for two stimuli, one can calculate d _q , the distance between the means of the corresponding distributions in units of q. The value of q is, then,

$$ \frac{{\Delta D}}{{{{d}_q}}}, $$

where ΔD is the difference between the two stimulus durations in physical time units. The framework is illustrated in Fig. 1.

Fig. 1

Schematic illustration of the assumptions behind Kristofferson’s (1980) data processing. The distribution of noise in the representation of durations D ₂ and D ₃ is described by an isosceles triangle with base 2q. The probability of a “long” response is given by the area of the triangle to the right of the criterion D _c . The difference between the means of the two distributions in units of q is denoted d _q and can be calculated from the observed response proportions. (This model was presented by Allan & Kristofferson [1974a]. Kristofferson [1977, 1980] proposed a real-time criterion-setting theory of duration discrimination that conceptualizes the framework in a slightly different way but which retains the same core structure, so that the estimation of q remains the same)

Kristofferson (1980) assumed that D ₁ and D ₄ (the two most widely spaced durations in each set) were perfectly discriminable and that errors on these trials represented a failure to process the stimulus. He calculated the probability of processing the stimulus as $K = P\left( {L\left| {{{D}_4}} \right.} \right) - P\left( {L\left| {{{D}_1}} \right.} \right)$, where$P\left( {L\left| {{{D}_i}} \right.} \right)$ is the observed proportion of “long” responses to a stimulus with duration D _i . The probability of making a “long” response, given failure to process the stimulus, is estimated by

$$ \beta = \frac{{P\left( {L\left| {{{D}_1}} \right.} \right)}}{{1 - K}}. $$

Kristofferson (1980) estimated these parameters for each base duration, using the data from sessions 11–15, and used them to correct the response probabilities for the subsequent sessions (16–20). He then used these corrected probabilities to estimate q for sessions 18, 19, and 20, obtaining separate estimates of q from the D ₂ versus D ₃ and D ₅ versus D ₆ discriminations and averaging them.

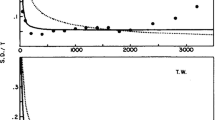
The average q values from Kristofferson’s (1980) experiment are plotted as black circles in the top left panel of Fig. 2. The data have a “staircase” structure, with segments that are relatively flat interspersed by large jumps at approximately 200, 400, and 800 ms. It is also instructive to examine the separate values of q estimated from the D ₂ versus D ₃ and D ₅ versus D ₆ discriminations (labeled q ₂₃ and q ₅₆, respectively). Kristofferson tabulated but did not plot these values, which are shown in the lower panels of Fig. 2. Here, it is conspicuous that the staircase pattern is really evident only for the D ₂ versus D ₃ discrimination; the values of q ₅₆ show a single discontinuity at 800 ms, with little indication of the “steps” at 200 and 400 ms.

Fig. 2

Estimates of the “time quantum” q from Kristofferson (1980). Kristofferson used corrected response probabilities to calculate two q values for each of sessions 18–20, one (which we label q ₂₃) based on the discrimination of D ₂ and D ₃ and the other (labeled q ₅₆) based on the discrimination of D ₅ and D ₆. These values were averaged to give an overall estimate of q for each base duration; these estimates are shown in the top left-hand panel. The two panels below show the separate mean estimates of q ₂₃ and q ₅₆. The right-hand panels show the results of slightly changing the estimation procedure by (a) using uncorrected response probabilities and (b) pooling the response probabilities from sessions 18–20 to obtain a single estimate of q ₂₃ and q ₅₆ at each base duration. These alternative estimates are shown as gray triangles, superimposed on the values calculated using Kristofferson’s method. The bottom left panel illustrates Kristofferson’s argument for “time quantum doubling.” The black dots reproduce the mean estimates of q from the top left panel. The dashed line shows the relationship between q and base duration early in training (sessions 1–5). To obtain the solid line segments, the data were mapped into the 400- to 800-ms range of base durations by appropriate doubling/halving of both coordinates, and the best-fitting line through these points was then converted back to the original scale. The graph suggests that q is the same shallow linear function of duration across the whole range, but that q doubles at base durations of approximately 200, 400, and 800 ms

Kristofferson (1980) analyzed the staircase pattern of q values in more detail. He noted that both the width of the flattish segments (the “treads” of the staircase) and the size of the jumps (the height of the staircase “risers”) approximately double as the base duration increases. That is, q ≈ 13, 25, 50, and 100 ms for base durations of 100–200, 200–400, 400–800, and 800–1,600 ms, respectively. To make this point graphically, Kristofferson prepared a plot like that in the bottom left panel of Fig. 2. The solid lines were obtained by scaling the base durations and q values to lie in the range 400–800 ms (values for base durations 100–200, 200–400, 400–800, and 800–1,600 ms were multiplied by 4, 2, 1, and 0.5, respectively), finding the best-fitting line through these data points, and then scaling this back up so that, for example, the height of the segment at 800 ms is twice that of the segment at 400 ms. It can be seen that the data are well-described by a function in which the slope of each segment is constant but there are jumps in q which double in size with every doubling of the base duration. R ² for this step-function is .99.

The bottom left panel of Fig. 2 also has a dashed line showing the relationship between q and base duration for the first five sessions of training (based on uncorrected response probabilities for the D ₂ vs. D ₃ discrimination from the first five sessions at each base duration). With prolonged practice, the q values seem to unfold from this original discrimination function to reveal a quantal step function in discrimination performance.

Two aspects of the foregoing data analysis proved problematic when applied to our own data. First, participant F.M.S. made more errors when discriminating D ₁ and D ₄ than would be expected from failure to process the stimuli because of lapses of attention (c. 20% errors for some base durations), suggesting that these items are not perfectly discriminable and are “inside the psychophysical range” for this participant. In addition, for participant W.M., K was frequently 1.0, so that β could not be estimated. Second, Kristofferson’s (1980) calculations assume that the probability of a “long” response is always less than .5 for D ₂ and D ₅ but more than .5 for D ₃ and D ₆. This assumption was not met when separate response probabilities were calculated for each of sessions 18–20, but it was met when the response probabilities for those sessions were pooled before parameter estimation. It is therefore helpful to see how different Kristofferson’s data look when the q values are based on uncorrected probabilities that are pooled for sessions 18–20, rather than using corrected probabilities to calculate separate q values for each session and then averaging them. (Kristofferson’s uncorrected response probabilities for each session can be calculated from his reported parameter values.) These alternative q values are shown as gray triangles in the top right panel of Fig. 2, superimposed on the values used by Kristofferson for ease of comparison. Clearly, the uncorrected pooled probabilities produce estimates that are similar to the published values. In particular, the staircase structure is still clearly visible. Therefore, when analyzing our own data, we used uncorrected response probabilities pooled for sessions 18–20.

The top two panels of Fig. 3 show the mean q values for each participant; the lower panels show the separate q values based on the D ₂ versus D ₃ and D ₅ versus D ₆ discriminations. Inspection suggests some possible indication of a step function, but nothing that is very consistent either within or between participants. An eyeball test of the W.M. data gives the impression of some clear steps in the q ₅₆ data, but this is less apparent in the other two W.M. panels, particularly at longer durations. Indeed, there seem to be two linear functions in each panel, with a transition point at 740 ms. For F.M.S., inspection suggests some clustering in the data. One might argue that the mean q values (upper right panel) are grouped into triplets, although this breaks down somewhat for the shortest durations in the middle panel (based on the D ₂ vs. D ₃ discrimination) and more severely for the seven highest base durations in the bottom panel (based on the D ₅ vs. D ₆ discrimination). Notwithstanding these possible clusters in the data, the fact that q sometimes shows pronounced decreases with increasing base duration in the F.M.S. data is problematic.

Fig. 3

q values for W.M. (left column) and F.S.M. (right column). The top panel shows the mean q for each base duration; the bottom panels show q ₂₃ and q ₅₆. For W.M., the data are well-described by a quadratic function; for F.M.S., the data are approximately linear

For participant W.M., the mean q values (in milliseconds) are well-described by a quadratic line: $q = 13.20 + 64.53{{b}^2}$ (where b is the base duration, in seconds) has R ² = .993 (95% CIs: intercept, 10.00–16.40; b ², 60.81–68.24) . Adding a linear trend does not significantly improve the fit, whereas adding a quadratic term to the linear function does significantly improve the fit. For participant F.M.S., a straight line gives a fairly good fit: $q = 10.31 + 126.36b$ has R ² = .921 (95% CIs: intercept, −8.45–29.06; b, 101.75–150.99). Adding a quadratic term does not improve the fit, whereas adding a linear term to the quadratic fit does significantly improve the fit. For comparison, we applied the same regression analysis to Kristofferson’s (1980) published q values. Like F.M.S., his data are fairly well described by a straight line: $q = 3.46 + 92.63b$ has R ² = .945 (95% CIs: intercept, −7.84–14.76; b, 77.80–107.45) and adding a quadratic component does not significantly improve the fit.³

Figure 4 shows the results of applying the graphing strategy used by Kristofferson (1980) to our data. The top panels show the q values calculated from D ₂ and D ₃ during sessions 1–5, along with the best-fitting straight lines through the data. The middle panels show the results of scaling the data so that all base durations lie in the range 400–800 ms, as described above. The bottom panels show the mean q values from sessions 18–20; the dashed line is the regression line from the top panel, and the solid line segments were obtained by scaling the regression line from the middle panels. Contrary to Kristofferson’s results, there is very little indication of time quantum doubling in either participant’s data (compare these plots with the bottom left panel of Fig. 2).

Fig. 4

Examining whether q is a step function of base duration for W.M. (left columns) and F.M.S. (right columns). The top panels show the mean estimates of q based on the discrimination of D ₂ and D ₃ during the first five sessions at each base duration. The middle panels show the final q values from sessions 18–20 mapped onto the 400- to 800-ms range of base durations by appropriate doubling/halving of both coordinates, along with the best-fitting line through these points. The bottom panels are like the plot of Kristofferson’s (1980) data in the bottom left panel of Fig. 2, showing the final q values along with the regression line from the top panel and line segments based on the regression line of the middle panel. The R ² for these step-functions are .867 and .943 for W.M. and F.M.S., respectively

Fitting Gaussian psychometric functions

Cumulative Gaussian psychometric functions were fit to the data using maximum likelihood procedures.⁴ The fitting procedure involved estimating two parameters: the mean (M) and the standard deviation (SD) of the Gaussian curve. The mean indicates the physical duration at which the probability of a “long” response is .5 and is often referred to as the point of subjective equality. It is convenient to calculate the constant error, CE = M − base duration (i.e., how far above or below the base duration a stimulus must be for the probabilities of judging it “short” and “long” to be equal). More important for our purposes, the standard deviation of the fitted curve provides a measure of discrimination accuracy commonly used in time perception research (e.g., Getty, 1975; Grondin, 2005, 2008), and dividing SD by the base duration gives the Weber fraction, WF.

Figure 5 plots the results for participant W.M. The leftmost column shows the SD, WF, and CE values as a function of base duration for the first three sessions at each base duration (data from the three sessions were pooled prior to curve fitting). The central column shows the data from sessions 13–15, which were the last three sessions before moving to the more difficult stimulus set. The rightmost column shows the results from sessions 18–20, which were the last three sessions at each base duration. Figure 6 plots the corresponding values for participant F.M.S.

Fig. 5

Parameter estimates from fitting a cumulative Gaussian psychometric function to the data from participant W.M. The top panels show the standard deviation of the fitted curve, a measure of discrimination; the middle panels show the Weber fraction (the standard deviation of the fitted curve divided by the base duration); the bottom panels show the constant error (the difference between the physical duration for which the probability of a long response is .5 and the base duration). The leftmost column shows the data from the first three sessions at each base duration; the central column shows the data from the last three sessions before the change to the harder stimulus set; the rightmost column shows the data from the last three sessions at each base duration

Fig. 6

Parameter estimates from fitting a cumulative Gaussian psychometric function to the data from participant F.M.S. The layout is as for Fig. 5

For participant W.M., the plot of SD values against base duration is curvilinear, particularly for sessions 18–20. For sessions 1–3, the regression line $SD = 4.18 + 17.82b + 19.48{{b}^2}$(where b is the base duration, in seconds; SD is in milliseconds) provides a good description of the data, with R ² = .985 (95% CIs: intercept, −0.72–9.07; b, 1.70–33.94; b ², 8.86–30.11). Dropping either the linear or the quadratic term led to a significantly worse fit. For sessions 18–20, the data were well-described by $SD = 5.64 + 26.34{{b}^2}$, with R ² = .993 (95% CIs: intercept, 4.33–6.95; b ², 24.83–27.86); adding a linear term did not significantly improve the fit. This curvilinearity means that the Weber fraction is not constant —a fact illustrated by the central row of Fig. 5. The quadratic relationship between SD and base duration mirrors the pattern reported above for the estimates of q (compare Fig. 5 with the left column of Fig. 3.)

For participant F.M.S., the data were approximately linear. For the first three sessions, the SD values were somewhat noisy—mainly because of a very high value of SD for the 910-ms base duration—but the line $SD = 0.51 + 89.08b$ provided a reasonable description of the data (R ² = .780; 95% CIs: intercept, −23.43–24.45; b, 57.66–120.49); adding a quadratic term did not significantly improve the fit. By the last three sessions, the data were less noisy, with the line $SD = 4.37 + 55.76b$ having R ² = .923 (95% CIs: intercept, −3.79–12.53; b, 45.05–66.47). Again, adding a quadratic term did not significantly improve the fit, and the linear relationship between base duration and SD mirrors the pattern in the estimates of q reported above. Inspection of the Weber fractions in Fig. 6 suggests a weak negative correlation between WF and base duration, particularly for the last three sessions, but this effect missed significance, r(11) = −.54, p = .053.

Inspection of the constant errors suggests no obvious patterns, except that (1) the values for both participants seem to become less noisy with increased training, and (2) for both participants, the CE for the 1,480-ms base duration is particularly low—reflecting a tendency to respond “long” to stimuli whose duration is less than the base duration.

Finally, Fig. 7 allows direct comparison of the results from the 2 participants from sessions 18–20. Data from W.M. are shown as black circles; data from F.M.S. are gray triangles. In addition, the open circles show the results of fitting Gaussian psychometric functions to Kristofferson’s (1980) data. Kristofferson’s SD values approximate a linear function of base duration: the line $SD = - 0.10 + 45.58b$ has R ² = .972 (95% CIs: intercept, −4.03–3.84; b, 40.14–50.74) and is not improved by the addition of a quadratic term (consistent with the linear relationship between q and base duration reported above). Comparison of the data from the 3 participants shows that, even after extensive practice, there are pronounced individual differences in temporal discrimination.

Fig. 7

A comparison of the SD, WF, and CE values from the 2 participants. The data are from the last three sessions (18–20) at each base duration. Data from Kristofferson (1980) are included for comparison

Learning effects

To examine the effects of practice in more detail, the testing sessions for each base duration were grouped into consecutive pairs (i.e., sessions 1 and 2 formed one pair, sessions 3 and 4 formed another, and so on). Gaussian psychometric functions were then fitted to the pooled data from each pair of sessions (this pooling of consecutive sessions was necessary because the maximum likelihood fitting was sometimes unstable when applied to each session separately). Note that in all cases for W.M. and in most cases for F.M.S., the two sessions in a pair were conducted on the same day, so it is convenient to think of each session pair as one day in the testing regimen, and we sometimes use “day” as a shorthand for “pair of test sessions”.

To get an overall impression of how performance improves with practice, the SD and WF values were each averaged over base duration and plotted as a function of testing session (Fig. 8). For W.M., there is steady but very gradual linear improvement over time; for F.M.S., there is a large improvement in performance between the first and second days of testing, followed by a gradual and approximately linear improvement. Neither participant seems to have reached an asymptote in performance by the final day of testing.

Fig. 8

The effects of training on overall temporal discrimination. The top panel shows the change in the standard deviation of the cumulative Gaussian psychometric function, averaged over all base durations; the bottom panel shows the corresponding changes in the Weber fraction. Adjacent sessions at a given base duration were pooled, so session pair 1 refers to data from sessions 1 and 2, pair 2 refers to data from sessions 3 and 4, and so on. Each session pair typically corresponds to 1 day of training

Figure 9 shows the same data, but with separate learning curves for each base duration. (Adjacent base durations have been averaged together to reduce the complexity of the plot.) The form of the learning function does not obviously depend on base duration, but for both participants the change in SD with practice seems to be larger for longer durations (or equivalently, larger for durations for which initial performance is worse). This conclusion is supported by reasonably large correlations between base duration and the change in SD between day 1 and day 10: for W.M., Kendall’s τ = −.72, p < .001; for F.M.S., τ = −.41, p = .057. (The negative correlation coefficients mean that the reduction in SD between day 1 and day 10 was greater for longer base durations.) By contrast, the change in Weber fraction between the first day and the last seems to be independent of base duration: for W.M., τ = −.21, p = .367; for F.M.S., τ = .03, p = .952.

Fig. 9

The effects of training on discrimination, organized by base duration. The top panels show the change in SD; the lower panels show the change in WF. Data on the left are from W.M.; those on the right are from F.M.S. Parameter estimates for adjacent base durations have been averaged in order to keep the number of lines on the plots manageable

Kristofferson (1980) suggested that additional training may be required to produce stable performance. To explore this, W.M. completed an additional four sessions at the 1,480-ms base duration, using the same stimuli as those in sessions 16–20. (These extra sessions occurred straight after the main set and followed the same regimen as before.) The Weber fractions for sessions 20–24 were .043, .045, .041, .043, and .041, respectively, indicating little improvement. The WF dropped by 23.3% (from .056 to .043) between session 16 (the first session with the more difficult discrimination) and session 20; the drop between session 20 and session 24 was only 3.6%.

Does learning about one base duration transfer to the next? The experiment was not designed to answer this question, but a basic examination can be made by asking whether the WFs calculated from the first pair of sessions with each base duration decline as the experiment progresses. There was no evidence of a correlation between this early performance and the position of the base duration in the series for either participant (for W.M., τ = .13, p = .590; for F.M.S., τ = −.10, p = .675). This is perhaps unsurprising given that there was a break between completing each base duration and starting the next. We also asked whether the amount of learning that took place during the 20 sessions with a given base duration changed over the course of the experiment. For each base duration, we calculated both the absolute and proportional drop in the WF from the first pair of sessions to the last pair and asked whether these indices of learning correlate with the position of the base duration in the series (absolute drop = WF _Day10 − WF _Day1; proportional drop = absolute drop/WF _Day1). For F.M.S., neither correlation was significant (for absolute drop in WF, τ = .00, p = 1.000; for proportional drop in WF, τ = −.05, p = .858). For W.M., however, there was some indication that learning increased over the course of the experiment (for absolute drop in WF, τ = −.46, p = .030; for proportional drop, τ = −.41, p = .057). However, one must be cautious about interpreting this result, given that it is based on a single participant and a single sequence of base durations whose Weber fractions differ substantially.

Discussion

The present study provides information about three major issues. The first is directly related to the quantal hypothesis/demonstration of Kristofferson (1980). The second concerns the more general question of the relationship between timing variability and time magnitude. Finally, the data also provide a rich source of information about the benefits and limitations of extensive interval discrimination training.

Is there a time quantum?

Neither participant provided a convincing replication of the quantal step function reported by Kristofferson (1980). However, both the data collection and the data processing were slightly different from Kristofferson’s. Regarding the latter point, the fact that it was not possible to apply Kristofferson’s correction for guessing seems unlikely to be critical: First, his data show the step function even without this preprocessing (Fig. 2), and second, the data for W.M. suggest few lapses because discrimination was perfect in some sessions. The choice of a slightly different training regimen and procedure (two sessions per day rather than one, the decision not to use a warning signal) and differences in presentation (via in-ear headphones for W.M. and over a loudspeaker for F.M.S.) seem unlikely to exert a large influence in themselves, unless they affect the extent to which training produces asymptotic performance. On this point, the data are ambivalent. There is some indication that both participants were still learning in session 20 (see Fig. 8). On the other hand, the exploratory addition of four extra sessions at base duration 1,480 ms for W.M. produced very little improvement in discrimination. Moreover, Kristofferson’s performance is intermediate between that of the two present participants; W.M. shows noticeably superior discrimination, suggesting that the quantal step function does not simply emerge once a certain level of performance is reached. Perhaps the best we can say is that, if the quantal pattern is to emerge, it will require a truly exceptional amount of training. It is possible that Kristofferson’s (1976, 1977) extensive prior experience in this type of duration discrimination task meant that less training was needed to reach the asymptotic performance required for the step function to emerge.

In short, there is no clear-cut reason for the difference between our data and those of Kristofferson (1980). Two other points are worth noting. First, it is not really clear how convincingly Kristofferson’s own data demonstrate a step function. To be sure, the bottom panel of Fig. 2 (where lines illustrating the step function have been added to the data) is compelling, but when the regression lines are removed and the data from the two different discriminations (D ₂ vs. D ₃ and D ₅ vs. D ₆) are plotted separately, as in the other panels of Fig. 2, the pattern is less clear. It is not obvious that a researcher presented with the mean q values in the top left panel of Fig. 2 would think to develop the step function plot shown by Kristofferson; and to the extent that there is a step function, it seems to be entirely due to the D ₂ versus D ₃ discrimination and not the D ₅ versus D ₆ discrimination.

The second point to note is that, even if the step function in Kristofferson’s (1980) data does provide the best description of what happens when temporal discrimination reaches asymptote, it may not reflect a profound, intrinsic aspect of temporal processing. Table 1 shows durations D ₁ to D ₆ for each base duration. The rightmost columns show the differences between the pairs of durations used to calculate q. It is conspicuous that the locations of the doubling points in the step function coincide with the points where these differences change. For example, for base durations 100 and 160 ms, the difference between D ₃ and D ₂ is 20 ms, and the difference between D ₅ and D ₆ is 10 ms. For base durations 200, 250, and 350 ms (which make up the next step in Kristofferson’s step function), the differences are always 30 ms (D ₂ vs. D ₃) and 20 ms (D ₅ vs. D ₆)—and so on for the other two “steps.” There is evidence that temporal discrimination depends on the distribution of durations presented for judgment. Wearden and Ferrara (1995, 1996) and Brown, McCormack, Smith, and Stewart (2005) found that classifications of stimuli as “short” and “long” in a bisection task depended on the range (specifically, the ratio of the longest and shortest durations) and spacing of the stimuli (but see Grondin, 2010b). Thus, there is some chance that the purported time quantum doubling in Kristofferson’s data reflects the structure of the discriminated stimulus sets rather than a fundamental property of the nervous system.

Finally, it is worth mentioning that other research provides conflicting evidence regarding the quantization of temporal processing. Ulrich (1987), for example, reported an analysis of data from temporal order judgments which argues against the quantization of psychological time. However, Geissler and colleagues (e.g., Geissler, Schebera, & Kompass, 1999) have argued that data from apparent motion thresholds indicate a time quantum of about 4.5 ms and have developed a “taxonomic model of quantal timing” based on nested sets of oscillations.

Scalar timing

The present data can hardly be used to argue that there is a quantal step function for interval discrimination. Furthermore, they do not support any simple, universal description of the relationship between the discrimination threshold and the magnitude of the intervals to be timed (at least for the range 0.1–1.5 s).

A strict form of Weber’s law implies that the standard deviation of the psychometric function will increase linearly with base duration. Scalar expectancy theory similarly posits a constant Weber fraction. In many cases, the Weber fraction rises sharply as duration falls below some small limit (e.g., 0.2 s; see Getty, 1975). This can be explained by positing noise that is independent of stimulus magnitude and whose relative importance therefore diminishes as duration increases, giving rise to a generalization of Weber’s law.

For participant W.M., the standard deviation of the psychometric function is a curvilinear function of the base duration even early in practice, and by the last three sessions the curvature is pronounced, giving rise to a U-shaped relationship between the Weber fraction and base duration. The declining WF for short durations might be consistent with the modified version of Weber’s law, but the rise for durations longer than 1 s is not. Getty (1975) reported a rising Weber fraction for durations above about 2 s, and similar U-shaped patterns were found by Blakely (1933, cited in Woodrow, 1951) and Stott (1933, cited in Woodrow, 1951). More recently, Grondin (in press) has found a systematic increase in the Weber fraction between 1.0 and 2.0 s for empty auditory intervals, using discrimination, reproduction, and categorization tasks; Grondin’s article also provides a comprehensive review of other violations of the scalar property, and Grondin suggests a “temporal span” of perhaps about 1.3 s, beyond which the to-be-timed interval exceeds the capacity of working memory, necessitating a change in timing strategy and a corresponding shift in the relationship between timing variability and objective duration.⁵ Consistent with this, Bangert et al. (2011) observed a breakpoint at 1.25 s with a reproduction method.

The present data do not provide unequivocal support for this idea, however, because, for participant F.M.S., the standard deviation of the psychometric function appears to be approximately linearly related to base duration, and the Weber fraction shows, if anything, a gentle decrease with increasing base duration. Lewis and Miall (2009) have reported a similar negative relationship across a wider range of times (see also Matthews, 2011b; Matthews, Stewart, & Wearden, 2011). That the data for W.M. and F.M.S. show different patterns suggests that the issue of whether or not there is a constant Weber fraction for time over the range 100–1,500 ms is highly sensitive to individual differences, precise details of the experimental setup (e.g., whether the markers are presented over headphones or a speaker), or both.

The curvilinear pattern in W.M.’s Weber fraction data deserves a final comment (Fig. 5, middle panel). After training, the WF is lowest (and approximately constant) between 570 and 740 ms, suggesting a region of maximum temporal sensitivity. McAuley, Jones, Holub, Johnston, and Miller (2006) have developed a model of perceptual–motor timing that predicts such a U-shaped pattern (which they refer to as a restricted Weber function). In their entrainment model, timing accuracy deteriorates as the external period moves away from the period of an internal oscillator. In support of this, they found (1) that timing variability in a synchronize-tapping task follows a restricted Weber function, and (2) that there are age-dependent preferences for specific tempos, which they take to indicate the period of the latent oscillator. Interestingly, the preferred period for participants in the same age range as W.M. was 630 ms, which lies within the range of optimal sensitivity in the present experiment. It is not clear, however, whether the entrainment model can be extended to temporal discrimination, and there are reasons to doubt that timing is optimal at certain specific durations (Grondin, Ouellet, & Roussel, 2001).

Learning time

Our study provides a rare set of data on the effect of extensive training on duration discrimination. Allan and Kristofferson (1974a) described 5 observers who received extensive interval discrimination training, but only 1 participant was trained with intervals up to 910 ms, and, more important, performance over sessions was reported for only 1 participant for whom the longest intervals lasted 400 ms. For this naïve participant, there was some practice effect, occurring in the first few sessions, and there was no transfer from one stimulus range to another. The most systematic previous investigation (Rammsayer, 1994) revealed no practice effect for the discrimination of filled or empty intervals, but the data were restricted to a 50-ms standard.

Our data indicate that some improvement may be expected from extensive duration discrimination training, but this improvement remains modest and is more likely to occur with longer intervals. More important, while further practice would likely have improved performance and reduced the variability in the data, it seems unlikely that extended practice would uncover such fundamentally different patterns of performance as one may have expected following Kristofferson (1980).

Conclusion

We wanted to know whether extensive training on duration discrimination would reveal that the representation of time is based on quantal units—a finding that would be fundamental to our understanding of temporal information processing. Our data do not support Kristofferson’s (1980) quantal timing hypothesis. Of course, our data also do not definitively show that there are no internal time quanta. Nonetheless, and in spite of extensive training, the method we used did not indicate the presence of quanta for either a participant showing better discrimination levels than those in Kristofferson (1980) or a participant showing lower performance. Our data also challenge the notion of a constant Weber fraction for time, even within a restricted range of durations and after extensive training. Finally, our data show that the benefits of practice generally accrue slowly and are more pronounced for longer intervals than for shorter ones.