In a numerical comparison task in which participants have to judge, for example, whether a numerosity is inferior or superior to 5, reaction times (RTs) are longer and accuracy is lower when responding to numerosity “4” than to “1” (see Fig. 1a). This effect, known as the distance effect, refers to the fact that the longer the time required to judge whether two magnitudes differ the shorter the distance between the two magnitudes (Dehaene, 1996; Moyer & Landauer, 1967). Interestingly, numerical judgments based on symbolic information (i.e., digits) show a similar distance effect, revealing that numerical comparisons based on symbolic and nonsymbolic information might involve similar mechanisms and rely on analogous magnitude representation (Butterworth, 1999; Dehaene, 1997; Piazza, Pinel, Le Bihan, & Dehaene, 2007; Shuman & Kanwisher, 2004). At a neuronal level, numerical comparisons with symbolic and nonsymbolic information entail the activation of the horizontal segment of the intraparietal sulcus (Piazza et al., 2007). On the basis of this behavioral and neuroimaging evidence, a common magnitude system for number and numerosity has been proposed (Dehaene, 1996; Gallistel & Gelman, 1992, 2000; Piazza, Izard, Pinel, Le Bihan, & Dehaene, 2004). This system is supposed to underlie the transformation of discrete events into analogous representation of numerical magnitude (for a review, see Brannon, 2006; see also Pinel, Dehaene, Riviere, & Le Bihan, 2001; Pinel, Piazza, Le Bihan, & Dehaene, 2004). Symbolic numerical information would be automatically transformed into analogous magnitude representation (Dehaene, Dehaene-Lambertz, & Cohen, 1998). Some authors have suggested that this magnitude system could be involved in dimensions other than number, such as space and time, for instance (see Hubbard, Piazza, Pinel, & Dehaene, 2005; Kaufmann et al., 2005; Walsh, 2003). Although it still remains controversial to declare the existence of a shared magnitude representation system (Bueti & Walsh, 2009; Cappelletti, Freeman, & Cipolotti, 2009; Cohen Kadosh et al., 2005; Pinel et al., 2004), it seems commonly admitted that the mechanisms used for numerical magnitude comparison are similar to those used for physical comparison (Cantlon, Platt, & Brannon, 2009; Gallistel & Gelman, 1992, 2000). One piece of evidence accounting for this claim comes from the presence of the distance effect in any comparison task, regardless of the dimension (i.e., time, brightness, size, length). Indeed, in a line length comparison task, the more similar two stimuli appear, the slower responses are and the more errors are made (Fias, Lammertyn, Reynvoet, Dupont, & Orban, 2003; Fulbright, Manson, Skudlarski, Lacadie, & Gore, 2003; Johnson, 1939). Therefore, the distance effect seems to be an indicator of magnitude processing for numerical but also physical comparisons.

Fig. 1
figure 1

a Representation of the percentage of errors (%) in a number comparison task as a function of distance between standard (number 5 presently) and comparative stimulus (from 1 to 4 and 6 to 9) for digit numbers. b The graphs represent the percentage of errors (%) in a line length comparison task as a function of distance between standard and comparative stimuli for lines divided into two equal-sized parts and for lines divided into two different-sized parts. Note that in these two graphs, the four left-sided lines are physically shorter than the standard stimulus (a non-bisected line), whereas the four right-sided lines are physically longer. The increase in errors between the closest inferior and superior distances, causing a deviation towards the right, refers to an underestimation of comparative stimuli as compared to the standard stimulus (a non bisected line); in opposition, when errors decrease between the closest inferior and superior distances, producing a displacement towards the left, it mirrors an overestimation (see Charras & Lupiáñez, 2009, 2010)

Full size image

In the length comparison literature, it has recently been shown that line bisection modulates length estimation (see Charras & Lupiáñez, 2009, 2010; see also Künnapas, 1955; Wolfe, Maloney, & Tam, 2005). Length estimation of a line bisected into two equal-size parts is underestimated, whereas, in contrast, a line bisected into two different-sized parts is overestimated (Charras & Lupiáñez, 2009, 2010). In these tasks, a two-line configuration composed of a vertical and a horizontal line was briefly presented on every trial. The participant’s task was to determine which of the two lines was the longest (the horizontal or the vertical one). The two lines always shared a junction, since they crossed each other. Therefore, in order to perform the comparison task, participants had somehow to sum up the two either equal (symmetrically bisected lines) or different (asymmetrically bisected lines) parts of the line. Bisection into two equal versus different-sized parts clearly affected the point at which the lines were perceived as equal to each other. Bisection into two equal versus different-sized parts clearly affects the distribution of the distance effect. Indeed, by definition, the distance effect is an index of magnitude estimation, performance being worse at the closest distance. It predicts that if estimation is not biased (neither underestimation nor overestimation), performance is worse when the comparative stimuli are truly closer in magnitude to the standard stimulus, as is shown by the maximum error rate in Fig. 1a. However, if the comparative stimuli are underestimated (as with lines bisected into two equal-sized parts), the standard stimulus will appear close in magnitude to comparative stimuli that are superior in magnitude. Schematically, the error peak reflecting the point of perceived shorter distance (i.e., equality) will be displaced toward superior comparative stimuli (see Fig. 1b). In opposition, if the comparative stimuli are overestimated (as with lines bisected into two different-sized parts), the standard stimulus will appear close in magnitude to comparative stimuli that are inferior in magnitude, leading the error peak (i.e., the point of perceived shorter distance or equality) to be shifted toward inferior comparative stimuli (Fig. 1b).

On the basis of the fact that the distance effect is similar regardless of the dimension that is compared (from continuous and nonsymbolic to discrete and symbolic information), the objective of the present study was to test to what extent the summation biases observed in the magnitude representation of length (under and overestimations; Charras & Lupiáñez, 2009, 2010) could also be observed in the magnitude representation of numerical information. Therefore, we tested whether in number processing the sum of two equal parts is biased toward an underestimation (i.e., 26 + 26) and, conversely, whether the sum of two different parts is biased toward an overestimation (i.e., 24 + 28).

Behavioral parallels between line and number processing have previously been demonstrated in the literature. For instance, left unilateral neglect, which is characterized by a rightward spatial bias, affects both line and number processing because these two dimensions show similar spatial organizations (Rossetti et al., 2004; Zorzi, Priftis, & Umiltà, 2002). In the present study, our objective was to highlight a new parallel between line and number processing that was not based on their similar spatial organizations but rather on their commonalities in coding and comparing magnitudes (i.e., the distance effect; for a review, see Cantlon et al., 2009; Cohen Kadosh, Lammertyn, & Izard, 2008). Henceforth, in the following experiments, we explored whether summation biases could be observed in a number comparison task—that is, a task based on symbolic and discrete information. We matched the comparison task used with lines (Charras & Lupiáñez, 2009, 2010) to those used in the present study. Participants performed a number comparison task with Arabic digits in which the comparative stimulus could be an addition. Participants were asked to rapidly add the two numbers and to judge whether the sum was inferior or superior to a standard stimulus. Two types of addition were presented: In the repeated number condition, stimuli were repeated number additions (RN, e.g., 26 + 26), whereas in the different number condition, participants had to add two different numerals (DN, e.g., 24 + 28). We aimed at testing whether the sum “26 + 26” would be underestimated (i.e., judged as inferior to the standard stimulus 52), and the sum “24 + 28” overestimated (i.e., judged as superior to the standard stimulus 52). The distance effect was analyzed and used as an index of the comparison efficiency.

If, as was expected, RN additions were underestimated in the present experiments, the error peak reflecting the perceived shorter distance or equality would have been displaced toward superior stimuli in the RN condition. Consequently, we should have observed better accuracy for inferior than for superior stimuli (see Fig. 1b). In contrast, if DN additions were overestimated, we should have observed better accuracy for superior stimuli than for inferior ones (see Fig. 1b).Footnote 1

Experiment 1

In the present experiment, two distances between standard and comparative stimuli were used (four units and two units) that were either inferior or superior (n - 4, n - 2, n + 2, n + 4). This manipulation aimed at highlighting a distance effect—that is, better performance for a four-unit distance than for a two-unit distance (either inferior or superior). And, as was explained above, our objective was to test whether performance drops for RN additions between inferior and superior distances (n - 2 > n + 2), in opposition to DN additions, in which we expected performance to improve between inferior and superior distances (n - 2 < n + 2).

Method

Participants

Sixteen undergraduate students (one male) from the University of Granada participated voluntarily in this experiment in exchange for course credits. The mean age was 20 years old (range from 18 to 24). All participants reported to have normal or corrected-to-normal vision and all were naive as to the purpose of the experiment. The experiments reported presently were conducted in accordance with the ethical guidelines laid down by the Department of Experimental Psychology, University of Granada.

Apparatus and stimuli

Participants entered a dimly lit room and sat down in front of a computer screen at a distance of about 60 cm. A PC computer running E-Prime software (Schneider, Eschman, & Zuccolotto, 2002) controlled the presentation of the stimuli, timing operations, and data collection. A fixation point, a silver colored dot (font, Courier New and bold; size, 18 pt), was displayed at the center of the screen and was removed during the intertrial delay. Digit numbers were presented using Arabic numerals and always appeared above fixation. They were written in Courier New font with a point size of 18. To differentiate standard and comparative stimuli, which were only separated by an empty black background display, the standard stimulus was written in green, and the comparative stimulus in white. The participants’ task was to judge whether the comparative stimulus was inferior to the standard stimulus, in which case, they were to press the “c” key with their left hands, or superior, in which case they were to press the “b” key with their right hands (two forced choices response). Given that responses to numerical magnitude are spatially associated, being much easier to respond “inferior” with the left hand and superior with the right one (Snarc effect, see Dehaene, Bossini, & Giraux, 1993; Gevers, Lammertyn, Notebaert, Verguts, & Fias, 2006), response keys were not counterbalanced between participants.

The standard stimulus was a two-digit number whose value was 48, 50, 52 or 54, and varied from trial to trial within the same block.

The comparative stimulus could be a single number (SN) or an addition. More precisely, two types of additions were manipulated: repeated number additions (RN, i.e., 24 + 24) and different number additions (DN, i.e., 22 + 26). Independently of the comparative stimulus type (SN, RN, and DN), the standard-comparative stimuli distance (S–C) was of “-4 units,” “-2 units,” “+2 units,” or “+4 units”. For instance, using the standard stimulus 54, the comparative stimulus could assume one of the following values: 50, 52, 56, or 58 (n - 4, n - 2, n + 2 or n + 4). The set of stimuli used in the present study is detailed in Table 1.

Table 1 Stimuli used in Experiments 1 and 2
Full size table

In the DN condition, the numbers’ location in the additions was controlled, so that the smaller number was displayed on the left of the “plus” sign on half of the trials, and on the right on the other half. To equate the total of trials between the three types, SN and RN comparative stimuli were presented twice. As was mentioned above, the standard stimulus had four different values so as to prevent participants from learning the sum of additions and also to weaken target–response associations. For instance, the comparative stimulus “26 + 26” triggered the response “superior” when compared to 50, but the response “inferior” when compared to 54. The standard stimulus manipulation could obviously not eliminate the advantage of practice, but at least it reduced it. The same trial was repeated only six times.

Procedure

Every trial began with the appearance of a fixation point for a variable period of time (between 1,000 and 1,500 ms). Then, the standard stimulus was presented for 100 ms, after which it disappeared. After a variable duration of 900 or 1,100 ms (black screen), the comparative stimulus appeared for 500 ms. The fixation point was removed during response time. Participants had 2,500 ms to judge whether the comparative stimulus was inferior or superior to the previously presented standard stimulus. If no response was emitted during this time, a no-response feedback sentence (“too late”) was displayed on the screen. Feedback was provided for incorrect responses during practice; the word “NO!” written in red appeared on the screen when the response was incorrect.

Design

The experiment had a 3 (type of comparative stimulus) × 4 (S–C distance) design with the two factors manipulated within participants. Comparative stimuli could be an SN, an RN, or a DN. The S–C Distance varied between n - 4, n - 2, n + 2, n + 4.

Participants performed 20 practice trials before beginning the experimental block composed of 288 trials (24 per experimental condition). Every 48 trial, a short break was allowed.

Results and discussion

Data from two participants were removed from the analysis since they did not reach 80% accuracy in the SN condition. We submitted accuracy (% of correct responses) and mean RTs to repeated measures ANOVAs, with the factors 3 (type of comparative stimulus) × 4 (S–C distance).

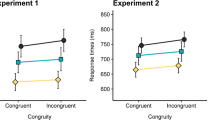
The analyses showed a main effect of type of comparative stimulus on accuracy and RTs, F(2, 26) = 26.51, p < .001, n² = .67, and F(2, 26) = 89.90, p < .001, n² = .87 (see Fig. 2), revealing that performance was better for SN than for RN, F(1, 13) = 23.92, MSE = 47, p < .001, for accuracy, and F(1, 13) = 85.88, MSE = 67515, p < .001, for RTs; and for RN as compared with DN, F(1, 13) = 18.85, MSE = 111, p < .001, for accuracy, and F(1, 13) = 27.61, MSE = 22,061, p < .001, for RTs. We also found the expected effect of S–C distance, F(3, 39) = 12.29, p < .001, n² = .49, for accuracy, and F(3, 39) = 6.52, p = .001, n² = .33, for RTs. To more specifically analyze the distance effect, the n - 4 and n + 4 conditions were grouped and compared to the n - 2 and n + 2 conditions. The planned comparisons showed that, as was expected, performance was better for the four-unit than for the two-unit condition, indicating a clear distance effect, F(1, 13) = 10.89, MSE = 63.89; p = .005; F(1, 13) = 28.62, MSE = 4159, p < .001, respectively, for accuracy and RTs; see Table 2).

Fig. 2
figure 2

Representation of errors (%) and mean RTs (ms) for the three types of comparative stimulus as a function of the S–C distance in Experiment 1

Full size image
Table 2 Means (M) and standard deviations (SD) of accuracy (in percentages) and reaction times (RTs, in milliseconds) as a function of type of comparative stimulus and S–C distance in Experiments 1 and 2
Full size table

More importantly, the interactions between type of comparative stimulus and S–C distance were also significant, F(6, 78) = 9.21, p < .001, n² = .41, for accuracy, and F(6, 78) = 5,65, p < .001, n² = .30, for RTs. To test whether, as was predicted, performance was better for n - 2 than for n + 2 distance in the RN condition but was worse for n - 2 than for n + 2 in the DN condition, we conducted planned comparisons. We first observed that there was no difference between n - 2 and n + 2 in the SN condition (Fs < 1 for accuracy and RTs). For RN additions, planned comparisons showed that performance to n - 2 and n + 2 was not statistically different, F(1, 13) = 1.08, MSE = 35.89, p = .32, and F < 1 for accuracy and RTs, whereas for DN additions, a superior distance advantage (n - 2 < n + 2) was observed on accuracy and RTs, F(1, 13) = 20.01, MSE = 149.05, p < .001, and F(1, 13) = 15.59, MSE = 14,848, p = .002 respectively).

Therefore these results are partly in line with our predictions, given that we did observe a DN overestimation, but no RN underestimation. A Stroop-like effect could have led to the lack of RN underestimation. Indeed, the standard stimulus was always a two-digit single number (“52”), whereas additions were composed of two numbers of two digits and a plus sign (“26 + 26”). Consequently, the physical size was much bigger for comparative than for standard stimuli. And, as was described in the literature, the discrepancy between physical size and numerical value can produce a Stroop-like effect (Pinel et al., 2004; Tzelgov, Meyer, & Henik, 1992). Thus, additions might be overestimated in the RN and DN conditions because stimuli constituting the comparative stimuli were physically larger than those constituting the standard stimulus. This Stroop-like effect might have accentuated the DN overestimation, but eliminated the RN underestimation. To test this assumption, we conducted Experiment 2 in which the standard stimulus was not visually presented.

Experiment 2

The objective of Experiment 2 was similar to that of Experiment 1, in the sense that we expected an underestimation of RN and an overestimation of DN. As in Experiment 1, a number comparison task was used in which comparative stimuli could be SN, RN, or DN. However in Experiment 2, the standard stimulus was not visually presented. Participants were instructed as to what was the standard stimulus at the beginning of the experiment (which was kept constant throughout the experiment). Two standard stimuli were used (45 vs. 53, manipulated between subjects; see Table 1). Note that most of the superior additions for the standard stimulus 45 became the inferior additions for the standard stimulus 53. Since our objective was to compare inferior to superior additions separately for RN and DN additions, this manipulation canceled out possible issues about the digit numbers that were used (i.e., compatibility effect; Nuerk, Weger, & Willmes, 2001, 2004). And, finally, to obtain a more pronounced distance effect, we used a larger scale of stimuli (from n - 27 to n + 27 in 14 steps).

Method

Participants

Twenty-one undergraduate students from the University of Granada participated voluntarily in this experiment in exchange for course credits. The participants’ age ranged from 19 to 41 years (mean age 21).

Apparatus and stimuli

A fixation point, a silver colored dot (font, Courier New and bold; size, 25), was displayed at the center of the screen. Digit numbers were Arabic numerals (font, Courier New and bold; size, 15) that always appeared above fixation. The participants’ task was to judge whether the comparative stimulus was either inferior to the standard stimulus, in which case they were to press the “v” key with their right index fingers, or superior, in which case they were to press the “b” key with their right middle fingers (Spanish keyboard, in which the “v” is to the left of the “b”). As in the previous experiment, comparative stimuli could be either a SN, or a sum of RN or DN. However, in this experiment, SN stimuli were presented separately in the starting and final blocks. RN and DN stimuli were mixed within the same block and were presented between the starting and final blocks. Independently of the type (SN, RN, DN), the S–C distance was of “27 units,” “19 units,” “11 units,” “7 units,” “5 units,” “3 units,” or “1 unit,” either inferior or superior to the standard stimulus. To equate the material between RN and DN conditions, two standard stimuli were used (either 45 or 53) but were counterbalanced between participants (see Table 1)—that is, each participant received only one standard stimulus.

Procedure

Every trial began with the appearance of a fixation point for a period of 1,000 ms and was followed by the comparative stimulus for 500 ms. During the response time delay, the fixation point was removed. Participants had to judge whether the comparative stimulus was inferior or superior to the standard stimulus (either 45 or 53) within a time window of 3 s.

Design

The experiment had a 3 (type of comparative stimulus) × 14 (S–C distance) design with the two factors manipulated within participants. Participants performed 20 practice trials before beginning the experimental block composed of 336 trials (eight repetitions of each trial).Footnote 2

Results and discussion

RTs faster than 300 ms and longer than 2,700 ms were removed from data analysis (1.45% of the trials). We then conducted repeated measures ANOVAs for accuracy and RTs with the factors type (SN, RN, DN) and S–C distance (14 levels).Footnote 3 The main effects of type and S–C distance were significant, F(2, 40) = 17.63, p < .001, n² = .47, and F(13, 260) = 21.10, p < .001, n² = .51, respectively, for accuracy; F(2, 40) = 33.70, p < .001, n² = .63, and F(13, 260) = 36.22, p < .001, n² = .64, for RTs. The type effect showed that SN were more easily solved than RN, F(1, 20) = 5.53, MSE = .02, p = .02, for accuracy, and F(1, 20) = 41.26, MSE = 121326, p < .001, for RTs, which were more easily solved than DN, F(1, 20) = 13.73, MSE = .01, p = .001, for accuracy, and F(1, 20) = 14.76, MSE = 78,232, p = .001 for RTs. The main effect of S–C distance refers to the distance effect: Performance is better for the farthest than for the closest S–C distances. To explicitly test the effect of distance on performance, we performed planned comparisons for accuracy and RTs in which the three farthest conditions (n27, n19, n11; for both inferior and superior) were grouped and compared to the three closest conditions (n5, n3, n1; for both inferior and superior). The planned comparisons confirmed that performance is better for the three farthest than for the three closest S–C distances, F(1, 20) = 99.88, MSE = .03, p < .001, for accuracy, and F(1, 20) = 84.93, MSE = 97,046, p < .001, for RTs.

Importantly, the interactions between the two factors were also highly significant, F(26, 520) = 2.91, p < .001, n² = .13, for accuracy, and F(26, 520) = 3.49, p < .001, n² = .15, for RTs. We performed planned comparisons for the two closest inferior conditions (n - 3, n - 1) versus the two closest superior conditions (n + 1, n + 3) separately for SN, RN, and DN. No difference was observed for the SN condition between inferior and superior distances, Fs < 1, n.s. for accuracy and RTs). In the RN condition, although accuracy was statistically similar for inferior (n - 3 and n - 1) and superior (n + 3 and n + 1) distances (Fs < 1), a significant effect was observed on RTs, F(1, 20) = 4.20, MSE = 47,238, p = .05. Responses were faster for inferior than for superior distances. In contrast, for the DN condition, accuracy was greater for superior distances than for inferior ones, F(1, 20) = 8.05, MSE = .05, p = .01, whereas there was no significant difference in RTs, F(1, 20) = 1.11, MSE = 49,146, p = .30, n.s.

Although these results suggest a RN underestimation and a DN overestimation, we further analyzed the data by computing the point of subjective equality (PSEFootnote 4) for every type of comparative stimulus. We then conducted a repeated measures ANOVA with the factor type (SN, RN, DN). A main effect of type was found, F(2, 40) = 6.79, p = .003, n² = .25 (see Fig. 3). Planned comparisons showed that the PSE of DN additions was statistically different from that of RN additions, F(1, 20) = 15.59, MSE = 3.76, p < .001, confirming that DN stimuli were overestimated as compared with RN stimuli. Single mean t tests indicated that the PSE in the SN condition was not different from 0, t(20) = −0.97, p = .35, indicating that SN stimuli were well estimated. However, the PSE of DN additions (−1.30) tended to be inferior to 0, revealing an overestimation, t(20) = −1.96, p = .06), whereas the PSE of RN additions (+1.06) was superior to 0, suggesting an underestimation, t(20) = 2.11, p = .05.

Fig. 3
figure 3

Representation of errors (%) and mean RTs (in milliseconds) for the three types of comparative stimulus as a function of the S–C distance in Experiment 2

Full size image

General discussion

Nowadays, converging evidence has led us to think that humans might have a general system to represent and compare magnitudes approximately regardless of the dimension (for a review, see Cantlon et al., 2009). In everyday life, we constantly have to estimate distance, time, and numerosity to make decisions according to approximate magnitude representations—for example.–“Which is the shortest way to get to my office?” “Do I have time to buy the newspaper before my train leaves?” It has been argued that the comparison process of any continuous variables shows common signatures, such as the distance and size effects (for a review, see Bueti & Walsh, 2009; Cantlon et al., 2009; Cohen Kadosh et al., 2008; Hubbard et al., 2005; Walsh, 2003).

In the present investigation, we wanted to explore how summation biases magnitude estimation as indexed by the distribution of the distance effect. Recent studies have reported that line length comparisons are biased toward an underestimation when summing two identical-sized parts and toward an overestimation when the two parts are different in size (Charras & Lupiáñez, 2009, 2010). In the present study, we further explored whether summation also affects the representation of approximate magnitude when information is conveyed by symbolic and discrete information—that is, digit numbers. Instead of using a continuous and nonsymbolic dimension, a number comparison task was used in which participants had to rapidly judge whether the sum of two large numbers under Arabic digit notation was inferior or superior to a standard stimulus. Large numbers were used in order to avoid retrieving the sum from memory and hence encouraging the representation of approximate magnitude.

First, the results of the two experiments have clearly provided evidence that RN additions are more easily and accurately solved than DN additions, as indexed by a larger percentage of errors and longer RTs. In the literature of numerical cognition, it is well established that performance at adding two single digits is characterized by a reliable advantage in both latency and accuracy for two repeated-number additions as compared with two different-number additions (i.e., 8 + 8, called a “tie problem,” vs. 9 + 7, called a “nontie problem,” see Ashcraft, 1995; Groen & Parkman, 1972; Lefevre, Sadesky, & Bisanz, 1996). The fact that repeated and different number additions are not uniform in difficulty is referred to as the tie effect (Campbell, 1999; Campbell & Graham, 1985; Campbell & Gunter, 2002; Clapp, 1924; Lefevre & Liu, 1997). So far, to our knowledge, the tie effect was considered to be specific of small numbers. Indeed, this advantage was supposed to rely on direct memory retrieval (Lefevre, Shanahan, & DeStefano, 2004). However, it seems hard to believe that in the present experiments sums were retrieved from memory.Footnote 5 Another account for the tie effect stresses encoding facilitation (Blankenberger, 2001). And, by definition, it assumes that problem size should not affect the tie effect. The general advantage of RN as compared to DN, observed in the present study, directly questions the nature of the tie effect, since large-number additions appear to be also influenced by number repetition. But, besides the general advantage for RN, our results show that the type of comparative stimulus (RN vs. DN) highly affects the distribution of the distance effect (see Fig. 3). Indeed, summation biased the global representation of approximate magnitude toward an underestimation when they were identical, and toward an overestimation when the numbers to be added were different.

In this context, it is worth noting that recently McCrink, Dehaene, and Dehaene (2007) reported that computation of additions yields to an overestimation, in opposition to subtractions that produce an underestimation; this is referred to as the operational momentum effect (OM). On the basis of evidence supporting close associations between space and number, and more specifically on the spatially organized mental representation of numerical magnitude, these authors have suggested that addition processing is biased toward the right on the mental number line, mirroring an overestimation, whereas subtraction process is biased toward the left, congruent with an underestimation (see also Knops, Viarouge, & Dehaene, 2009; McCrink & Wynn, 2009; Pinhas & Fischer, 2008). This account implies that the OM effect is determined exclusively by the operator. However, our results provide evidence that the nature of the operands might also be critical (see also Cordes, Gallistel, Gelman, & Latham, 2007). One could consider that the under- and overestimation effects reported presently and the OM effect are additive, both acting on approximate calculation during additions. Whereas the nature of operation (addition, in contrast with subtraction) induces an overestimation bias, the nature of the operands to be added (RN vs. DN) could induce either an overestimation (in the case of DN) or an underestimation (in the case of RN). If operands (RN vs. DN) and operator (addition) biases acted independently on performance, we should get an enhanced overestimation of DN, since both biases would act in the same direction, and a reduced or absent underestimation of RN, since the underestimation induced by the operands would be compensated by the overestimation induced by the operator. The overall pattern of results observed in our two experiments seems to accommodate this hypothesis, although further investigation will be needed to specifically test this proposal.

At this point, one might wonder why the comparison process is biased toward an underestimation for sums of repeated stimuli and toward an overestimation for sums of different stimuli. In the following section, we have attempted to provide a tentative account. On the basis of the fact that the two stimuli in the repeated-number condition are by definition identical, we hypothesize that they might be processed as a single (repeated) stimulus. We propose that their processing requires less computation/cognitive effort, since there is no need to build a separate representation for each addend, as compared with DN additions, for which each operand needs to be represented. A heuristic linking cognitive effort and magnitude estimation could then account for the RN and DN effects. The easiness of representing RN additions could be due to the fact that they can be represented as a single repeated stimulus (i.e., plus a duplication sign). Although further research is needed to better understand the effect of stimulus repetition on magnitude estimation, it seems already uncontroversial that repeated stimuli are not processed in the same way as different stimuli. For instance, Xu and Chun (Xu, 2007, 2009; Xu & Chun, 2007, 2009), in accordance with the Kahneman’s object file theory (Kahneman, Treisman, & Gibbs, 1992), have recently argued that object perception runs through two phases: object individuation and object identification. Object individuation, which leads to “open” an object file, is limited to four events and is implemented in the inferior intraparietal sulcus (IPS); whereas object identification relies on the superior IPS. As a consequence, object perception should be impaired after bilateral parietal lesion, consistent with what can be observed in patients suffering from Balint’s syndrome. Xu (2009) also proposed that stimulus repetition has a special status, and she provided evidence that stimuli that were repeated on the same visual display were considered as distinct objects in the object individuation phase, but as a single object in the object identification phase. We propose to extend these notions to the case of magnitude estimation. If a stimulus is repeated, then the ease in processing identical stimuli or the cognitive gain in representing these objects may produce a magnitude underestimation as compared with different objects.

Obviously further research is needed to claim that the over- and underestimation effects are a new common signature that affects the comparison process. Nevertheless, the present article is, to our knowledge, the first piece of evidence supporting the idea of a general bias due to stimulus summation in the representation of approximate magnitude. It seems now necessary to gather more evidence supporting the modulation of the over- and underestimation effects over the magnitude comparison process and to elaborate a robust theoretical account supporting these effects.