Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The k-bend planar slope number of a family of planar graphs with maximum vertex-degree \(\varDelta \) is the minimum number of distinct slopes used for the edges when computing a crossing-free drawing with at most \(k > 0\) bends per edge of any graph in the family. For example, if \(\varDelta = 4\), a classic result is that every planar graph has a crossing-free drawing such that every edge segment is either horizontal or vertical and each edge has at most two bends (see, e.g., [2]). Clearly, this is an optimal bound on the number of slopes. This result has been extended to values of \(\varDelta \) larger than four by Keszegh et al. [15], who prove that \(\lceil \frac{\varDelta }{2}\rceil \) slopes suffice to construct a planar drawing with at most two bends per edge for any planar graph. However, if additional geometric constraints are imposed on the crossing-free drawing, only a few tight bounds on the planar slope number are known. For example, if one requires that the edges cannot have bends, the best known upper bound on the planar slope number is \(O(c^{\varDelta })\) (for a constant \(c > 1\)) while a general lower bound of just \(3\varDelta -6\) has been proved [15]. Tight bounds are only known for outerplanar graphs [17] and subcubic planar graphs [9], while the gap between upper and lower bound has been reduced for planar graphs with treewidth two [18] or three [10, 14]. If one bend per edge is allowed, Keszegh et al. [15] show an upper bound of \(2 \varDelta \) and a lower bound of \(\frac{3}{4}(\varDelta - 1)\) on the planar slope number of the planar graphs with maximum vertex-degree \(\varDelta \). In a recent paper, Knauer and Walczak [16] improve the upper bound to \(\frac{3}{2}(\varDelta - 1)\); in the same paper, it is also proved that a tight bound of \(\lceil \frac{\varDelta }{2}\rceil \) can be achieved for the outerplanar graphs.

In this paper we focus on the 1-bend planar slope number of directed graphs with the additional requirement that the computed drawing be upward, i.e., each edge is drawn as a curve monotonically increasing in the y-direction. We recall that upward drawings are a classic research topic in graph drawing, see, e.g., [1, 3, 11,12,13] for a limited list of references. Also, upward drawings of ordered sets with no bends and few slopes have been studied by Czyzowicz [4, 5]. We show that every series-parallel digraph (SP-digraph for short) G whose maximum vertex-degree is \(\varDelta \) has 1-bend upward planar slope number \(\varDelta \). That is, G admits an upward planar drawing with at most one bend per edge where at most \(\varDelta \) distinct slopes are used for the edges. This is shown to be worst-case optimal in terms of the number of slopes. An implication of this result is that the general \(\frac{3}{2}(\varDelta - 1)\) upper bound for the (undirected) 1-bend planar slope number [16] can be lowered to \(\varDelta \) when the graph is series-parallel. We then extend our drawing technique to undirected graphs and hence look at non-upward drawings. We show a tight bound of \(\lceil \frac{\varDelta }{2}\rceil \) for the 1-bend planar slope number of biconnected reduced SP-graphs and biconnected flat SP-graphs (see Sect. 2 for definitions). The biconnectivity requirement can be dropped at the expenses of one more slope. To prove the above results, we construct a suitable contact representation \(\gamma \) of an SP-digraph where each vertex is represented as a cross, i.e. a horizontal segment intersected by a vertical segment (Sect. 3); then, we transform \(\gamma \) into a 1-bend upward planar drawing \(\varGamma \) optimizing the number of slopes used in such transformation (Sect. 4). Our algorithm runs in linear time and gives rise to drawings with angular resolution at least \(\frac{\pi }{\varDelta }\), which is worst-case optimal. Some proofs and technicalities are omitted and can be found in [7].

2 Preliminaries

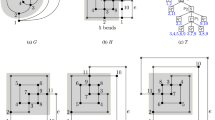
A series-parallel digraph (SP-diagraph for short) [6] is a simple planar digraph that has one source and one sink, called poles, and it is recursively defined as follows. A single edge is an SP-digraph. The digraph obtained by identifying the sources and the sinks of two SP-digraph s is an SP-digraph (parallel composition). The digraph obtained by identifying the sink of one SP-digraph with the source of a second SP-digraph is an SP-digraph (series composition). A reduced SP-digraph is an SP-digraph with no transitive edges. An SP-digraph G is associated with a binary tree T, called the decomposition tree of G. The nodes of T are of three types, Q-nodes, S-nodes, and P-nodes, representing single edges, series compositions, and parallel compositions, respectively. An example is shown in Fig. 1(a). The decomposition tree of G has O(n) nodes and can be constructed in O(n) time [6]. An SP-digraph is flat if its decomposition tree does not contain two P-nodes that share only one pole and that are not in a series composition (see, e.g., [8]). The underlying undirected graph of an SP-digraph is called an SP-graph, and the definitions of reduced and flat SP-digraph s translate to it.

The slope s of a line \(\ell \) is the angle that a horizontal line needs to be rotated counter-clockwise in order to make it overlap with \(\ell \). The slope of a segment is the slope of its supporting line. We denote by \(\mathcal S_k\) the set of slopes: \(s_i = \frac{\pi }{2} + i \frac{\pi }{k}\) (\(i=0,\dots ,k-1\)). Note that \(\mathcal S_k\) contains the slope \(\frac{\pi }{2}\) for any value of k. Also, any polyline drawing using only slopes in \(\mathcal S_k\) has angular resolution (i.e. the minimum angle between any two consecutive edges around a vertex) at least \(\frac{\pi }{k}\).

Fig. 1.
figure 1

(a) An SP-digraph G and its decomposition tree. (b) The safe-region (dotted) of a cross.

Full size image

3 Cross Contact Representations

Basic Definitions. A cross consists of one horizontal and one vertical segment that share an interior point, called center of the cross. A cross is degenerate if either its horizontal or its vertical segment has zero length. The center of a degenerate cross is its midpoint. A point p of a cross c is an end-point (interior point) of c if it is an end-point (interior point) of the horizontal or vertical segment of c. Two crosses \(c_1\) and \(c_2\) touch if they share a point p, called contact, such that p is an end-point of the vertical (horizontal) segment of \(c_1\) and an interior point of the horizontal (vertical) segment of \(c_2\). A cross-contact representation (CCR) of a graph G is a drawing \(\gamma \) such that: (i) Every vertex v of G is represented by a cross c(v); (ii) All intersections of crosses are contacts; and (iii) Two crosses c(u) and c(v) touch if and only if the edge (u, v) is in G.

We now consider CCRs of digraphs, and define properties that will be useful to transform a CCR into a 1-bend upward planar drawing with few slopes and good angular resolution. Let \(\gamma \) be a CCR of a digraph G with maximum vertex-degree \(\varDelta \). Let (u, v) be an edge of G oriented from u to v. Let p be the contact between c(u) and c(v). The point p is an upward contact if the following two conditions hold: (a) p is an end-point of the vertical segment of one of the two crosses and an interior point of the other cross, and (b) the center of c(v) is above the center of c(u). A CCR of a digraph G such that all its contacts are upward is an upward CCR (UCCR). An UCCR \(\gamma \) is balanced if for every non-degenerate cross c(u) of \(\gamma \), we have that \(|n_l(u) - n_r(u)| \le 1\), where \(n_l(u)\) (\(n_r(u)\)) is the number of contacts to the left (right) of the center of c(u). Let \(\{p_1,p_2,\dots ,p_\delta \}\) be the \(\delta \ge 0\) contacts along the horizontal segment of c(u), in this order from the leftmost one (\(p_1\)) to the rightmost one (\(p_\delta \)). Let t be the intersection point between the vertical line passing through \(p_\delta \) and the line with slope \(\frac{\pi }{2}-\frac{\pi }{\varDelta }\) and passing through \(p_1\). Similarly, let \(t'\) be the intersection point between the vertical line passing through \(p_1\) and the line with slope \(\frac{\pi }{2}-\frac{\pi }{\varDelta }\) and passing through \(p_\delta \). The safe-region of c(u) is the rectangle having t and \(t'\) as the top-right and bottom-left corner, respectively. See Fig. 1(b) for an illustration. If \(\delta =1\), the safe-region degenerates to a point, while it is not defined when \(\delta =0\). An UCCR \(\gamma \) is well-spaced if no two safe-regions intersect each other.

Drawing Construction. We describe a linear-time algorithm, UCCRDrawer, that takes as input a reduced SP-digraph G, and computes an UCCR \(\gamma \) of G that is balanced and well-spaced. The algorithm computes \(\gamma \) through a bottom-up visit of the decomposition tree T of G. For each node \(\mu \) of T, it computes an UCCR \(\gamma _\mu \) of the graph \(G_\mu \) associated with \(\mu \) satisfying the following properties: P1. \(\gamma _\mu \) is balanced; P2. \(\gamma _\mu \) is well-spaced; P3. Let \(s_\mu \) and \(t_\mu \) be the two poles of \(G_\mu \). If \(\mu \) is not a Q-node, then both \(c(s_\mu )\) and \(c(t_\mu )\) are degenerate, with \(c(s_\mu )\) at the bottom side of a rectangle \(R_\mu \) that contains \(\gamma _\mu \), and \(c(t_\mu )\) at the top side of \(R_\mu \).

Fig. 2.
figure 2

Illustration for UCCRDrawer. The safe-regions are dotted (and not in scale).

Full size image

For each leaf node \(\mu \) (which is a Q-node) the associated graph \(G_{\mu }\) consists of a single edge \((s_\mu ,t_\mu )\). We define two possible types of UCCR, \(\gamma _\mu ^A\) (type A) and \(\gamma _\mu ^B\) (type B), of \(G_\mu \), which are shown in Fig. 2(a) and (b), respectively. Properties P1 – P2 trivially hold in this case, while property P3 does not apply.

For each non-leaf node \(\mu \) of T, UCCRDrawer computes the UCCR \(\gamma _\mu \) by suitably combining the (already) computed UCCRs \(\gamma _{\nu _1}\) and \(\gamma _{\nu _2}\) of the two graphs associated with the children \(\nu _1\) and \(\nu _2\) of \(\mu \). If \(\mu \) is an S-node of T, we distinguish between the following cases, where \(t_{\nu _1} = s_{\nu _2}\) is the pole shared by \(\nu _1\) and \(\nu _2\).

  • Case 1. Both \(\nu _1\) and \(\nu _2\) are Q-nodes. Then an UCCR of \(G_\mu \) is computed by combining \(\gamma _{\nu _1}^A\) and \(\gamma _{\nu _2}^B\) as in Fig. 2(c). Properties P1 – P3 trivially hold.

  • Case 2. \(\nu _1\) is a Q-node, while \(\nu _2\) is not (the case when \(\nu _2\) is a Q-node and \(\nu _1\) is not is symmetric). We combine the drawing \(\gamma _{\nu _1}^A\) of \(G_{\nu _1}\) and the drawing \(\gamma _{\nu _2}\) of \(G_{\nu _2}\) as in Fig. 2(d). Notice that to combine the two drawings we may need to scale one of them so that their widths are the same. To ensure P1, we move the vertical segment of \(c(t_{\nu _1}) = c(s_{\nu _2})\) so that \(|n_l(t_{\nu _1}) - n_r(t_{\nu _1})| \le 1\). We may also need to shorten its upper part in order to avoid crossings with other segments, and to extend its lower part so that \(c(s_{\nu _1})\) is outside the safe-region of \(c(t_{\nu _1}) = c(s_{\nu _2})\), thus guaranteeing property P2. Property P3 holds by construction.

  • Case 3. If none of \(\nu _1\) and \(\nu _2\) is a Q-node, then we combine \(\gamma _{\nu _1}\) and \(\gamma _{\nu _2}\) as in Fig. 2(e). We may need to scale one of the two drawings so that their widths are the same. Property P1 holds, as it holds for \(\gamma _{\nu _1}\) and \(\gamma _{\nu _2}\). Furthermore, we ensure P2 by performing the following stretching operation. Let \(\ell _a\) and \(\ell _b\) be two horizontal lines slightly above and slightly below the horizontal segment of \(c(t_{\nu _1}) = c(s_{\nu _2})\), respectively. We extend all the vertical segments intersected by \(\ell _a\) or \(\ell _b\) until the safe-region of \(c(t_{\nu _1}) = c(s_{\nu _2})\) does not intersect any other safe-region. Property P3 holds by construction.

Let \(\mu \) be a P-node of T, having \(\nu _1\) and \(\nu _2\) as children (recall that neither \(\nu _1\) nor \(\nu _2\) is a Q-node, since G is a reduced SP-digraph). We combine \(\gamma _{\nu _1}\) and \(\gamma _{\nu _2}\) as in Fig. 2(f). We may need to scale one of the two drawings so that their heights are the same. Property P1 holds, as it holds for \(\gamma _{\nu _1}\) and \(\gamma _{\nu _2}\). To ensure P2, a stretching operation similar to the one described in Case 3 is possibly performed by using a horizontal line slightly above (below) the horizontal segment of \(c(s_\mu )\) (\(c(t_\mu )\)). Property P3 holds by construction.

To deal with the time complexity of algorithm UCCRDrawer, we represent each cross with the coordinates of its four end-points. To obtain linear time complexity, for each drawing \(\gamma _\mu \) of a node \(\mu \), we avoid moving all the crosses of its children. Instead, for each child of \(\mu \), we only store the offset of the top-left corner of the bounding box of its drawing. Afterwards, we fix the final coordinates of each cross through a top-down visit of T. The above discussion can be summarized as follows.

Lemma 1

Let G be an n-vertex reduced SP-digraph. Algorithm UCCRDrawer computes a balanced and well-spaced UCCR \(\gamma \) of G in O(n) time.

Fig. 3.
figure 3

(a)–(b) Transforming an UCCR into a 1-bend drawing. (c) An SP-digraph requiring at least \(\varDelta \) slopes in any 1-bend upward planar drawing.

Full size image

4 1-Bend Drawings

We start by describing how to transform an UCCR of a reduced SP-digraph into a 1-bend upward planar drawing that uses the slope-set \(\mathcal S_\varDelta \). Let \(\gamma \) be an UCCR of a reduced SP-digraph G and let c(u) be the cross representing a vertex u of G in \(\gamma \). Let \(p_1,\dots ,p_{\delta }\) (\(\delta \ge 1\)) be the contacts along the horizontal segment of c(u), in this order from the leftmost one (\(p_1\)) to the rightmost one (\(p_\delta \)). Let c be either the center of c(u), if c(u) is non-degenerate, or \(p_{\lfloor \delta /2 \rfloor +1}\) if c(u) is degenerate. Consider the set of lines \(\ell _0, \dots , \ell _{\varDelta -1}\), such that \(\ell _i\) passes through c and has slope \(s_i \in \mathcal S_\varDelta \) (for \(i=0,\dots ,\varDelta -1\)). These lines, except for \(\ell _0\), intersect all the vertical segments forming a contact with the horizontal segment of c(u). If c(u) is not degenerate, then \(\ell _0\) coincides with the vertical segment, which has at least one contact. In particular, each quadrant of c(u) contains a number of lines that is at least the number of vertical segments touching c(u) in that quadrant. Since \(\gamma \) is well-spaced, these intersections are inside the safe-region of c(u). Hence we can replace each contact of c(u) with two segments having slope in \(\mathcal S_\varDelta \) as shown in Fig. 3(a) and (b). More precisely, each contact \(p_i\) of c(u) is replaced with two segments that are both in the quadrant of c(u) that contains the vertical segment defining \(p_i\). This guarantees the upwardness of the drawing. Also, each edge has one bend, since it is represented by a single contact between a horizontal and a vertical segment and we introduce one bend only when dealing with the cross containing the horizontal segment. Finally, \(\varGamma \) is planar, because there is no crossing in \(\gamma \) and each cross is only modified inside its safe-region which, by the well-spaced property, is disjoint by any other safe-region. Thus, every reduced SP-digraph admits a 1-bend upward planar drawing with at most \(\varDelta \) slopes. To deal with a general SP-digraph, we subdivide each transitive edge and compute a drawing of the obtained reduced SP-digraph. We then modify this drawing to remove subdivision vertices (see also [7]).

Figure 3(c) shows a family of SP-digraphs such that, for every value of \(\varDelta \), there exists a graph in this family with maximum vertex-degree \(\varDelta \) and that requires at least \(\varDelta \) slopes in any 1-bend upward planar drawing. Namely, if a digraph G has a source (or a sink) of degree \(\varDelta \), then it requires at least \(\varDelta -1\) slopes in any upward drawing because each slope, with the only possible exception of the horizontal one, can be used for a single edge. In the digraph of Fig. 3(c) however, the edge (s, t) must be either the leftmost or the rightmost edge of s and t in any upward planar drawing. Therefore, if only \(\varDelta -1\) slopes are allowed, such edge cannot be drawn planarly and with one bend. Thus, the following theorem holds.

Theorem 1

Every n-vertex SP-digraph G with maximum vertex-degree \(\varDelta \) admits a 1-bend upward planar drawing \(\varGamma \) with at most \(\varDelta \) slopes and angular resolution at least \(\frac{\pi }{\varDelta }\). These bounds are worst-case optimal. Also, \(\varGamma \) can be computed in O(n) time.

Since every SP-graph can be oriented to an SP-digraph (by computing a so-called bipolar orientation [19, 20]), the next corollary is implied by Theorem 1 and improves the upper bound of \(\frac{3}{2}(\varDelta -1)\) [16] for the case of SP-graphs.

Corollary 1

The 1-bend planar slope number of SP-graphs with maximum vertex-degree \(\varDelta \) is at most \(\varDelta \).

Our drawing technique can be naturally extended to construct 1-bend planar drawings of two sub-families of biconnected SP-graphs using \(\lceil \frac{\varDelta }{2} \rceil \) slopes. Intuitively, if the drawing does not need to be upward, then for each cross c(u) (see e.g. Fig. 3(a)), one can use the same slope for two distinct edges incident to u. Also, the biconnectivity requirement can be dropped by using one more slope.

Theorem 2

Let G be a 2-connected SP-graph with maximum vertex-degree \(\varDelta \) and n vertices. If G is reduced or flat, then G admits a 1-bend planar drawing \(\varGamma \) with at most \(\lceil \frac{\varDelta }{2} \rceil \) slopes and angular resolution at least \(\frac{2\pi }{\varDelta }\). Also, \(\varGamma \) can be computed in O(n) time.

Corollary 2

Let G be an SP-graph with maximum vertex-degree \(\varDelta \) and n vertices. If G is reduced or flat, then G admits a 1-bend planar drawing \(\varGamma \) with at most \(\lceil \frac{\varDelta }{2} \rceil +1\) slopes and angular resolution at least \(\frac{2\pi }{\varDelta +1}\). Also, \(\varGamma \) can be computed in O(n) time.

5 Open Problems

We proved that the 1-bend upward planar slope number of SP-digraph s with maximum vertex-degree \(\varDelta \) is at most \(\varDelta \) and this is a tight bound. Is the bound of Corollary 1 also tight? Moreover, can it be extended to any partial 2-tree?