1 Introduction

Diffusion magnetic resonance imaging (DMRI) [1] is a non-invasive technique that allows reconstruction of white matter (WM) pathways by tracing the directional patterns of water diffusion. In connectomics, this involves tracing across gray-white matter boundaries in gyral blades of complex cortical convolutions [1]. To date, most tractography algorithms exhibit gyral bias with streamlines preferentially terminating at gyral crowns rather than sulcal banks or fundi. This bias can be observed even for high angular resolution diffusion imaging (HARDI) data [2, 3].

Local fiber orientations, commonly represented via fiber orientation distribution functions (FODFs), are usually assumed to be antipodal symmetric, even though in reality fiber tracts do not necessarily transverse each voxel in a symmetric fashion [4,5,6], especially in WM with complex configurations such as crossing, bending, bifurcation, kissing, and fanning [3]. In the cortex, a symmetric representation of orientations hinders the estimated streamlines from curving significantly to enter the cortical gray matter (GM). In this work, we demonstrate that asymmetric fiber orientation distribution functions (AFODFs) can potentially mitigate gyral bias in cortical tractography.

To date, asymmetric FODF estimation techniques [4, 5] have been mainly formulated in a voxel-wise manner. They are also not designed specifically to address the gyral bias problem. In this work, we introduce a global framework for AFODF estimation, dealing with partial volume effects that are prominent in tissue boundaries. We model the diffusion signal as the convolution of an AFODF with a multi-tissue response function [6]. The multi-tissue model accounts for signal contributions from white matter (WM), gray matter (GM), and cerebrospinal fluid (CSF).

In order to capture the asymmetry of the underlying fiber geometry in a local neighborhood, we extend the multi-tissue model to account for positive orientations (POs) and negative orientations (NOs). The AFODF at each voxel is estimated by enforcing orientation continuity across voxels. To understand the continuity constraint, we consider the scenario where a fiber leaves a voxel in a PO and enters a neighboring voxel in a NO. The constraint minimizes the difference between the PO and the NO. The AODFs are estimated globally across voxels, reducing sensitivity to noise. Unlike other global FODF estimation schemes [7, 8], our method is initialization independent and incorporates FODF asymmetry. Using in-vivo data, we demonstrate that the proposed method mitigates the effects of gyral bias and allows streamlines at gyral blades to make sharper turns into cortical GM.

2 Method

2.1 Asymmetric Fiber Orientation Distribution

The diffusion signal \(s_{p}(g)\) for gradient direction \(g \in \mathbb {S}^{2}\) and location \(p \in \mathbb {R}^3\) can be decomposed into \(M \in \mathbb {N}\) tissue types, each of which is characterized by an axially symmetric response function (RF) \(R_i (g,u)\) [6, 9]. The signal contribution of each tissue i in a voxel can be computed as the spherical convolution of its RF \(R_i (g,u)\) and the fiber orientation distribution function (FODF) \(F_{p,i} (u)\):

$$\begin{aligned} s_{p}(g) = \int _{u\in \mathbb {S}^2}\sum _{i=1}^{M} R_i(g,u)F_{p,i}(u) du, \end{aligned}$$
(1)

where the FODF is generally modeled using even order spherical harmonics (SHs). Due to the inherent antipodal symmetry of the FODF, i.e., \(F_{p,i}(u)=F_{p,i}(-u)\), \(u \in \mathbb {S}^2\), sub-voxel fiber fanning and bending cannot be distinguished using symmetric FODFs.

To circumvent the limitation of antipodal symmetry, we augment the multi-tissue constrained spherical deconvolution (CSD) [6] framework by incorporating information from neighbouring voxels \(\mathcal {N}_p\), allowing asymmetry in FODF estimation, giving us the AFODF. Based on fiber continuity, a fiber leaving the current voxel p with direction u should enter the next voxel \(q \in \mathcal {N}_p\) along its negative direction \(-u\) [4]. Based on this observation, the discontinuity of \(F_p(\cdot )\) in direction u can be measured by

$$\begin{aligned} \phi (p,u) = \left| F_{p}(u) - \frac{1}{K_{p,u}}\sum _{q \in \mathcal {N}_{p} } W(\langle \hat{v}_{p,q}, u\rangle ) F_{q}(u)\right| , \end{aligned}$$
(2)

where \(W(\langle \hat{v}_{p,q}, u\rangle )\) is a directional probability distribution function (PDF) that is related to the angular difference between u and \(\hat{v}_{p,q}= \frac{q - p}{\Vert q - p \Vert }\). \(K_{p,u} = \sum _{q \in \mathcal {N}_{p} } W(\langle \hat{v}_{p,q}, u\rangle )\) is a normalization term. We choose \(W(\langle \hat{v}_{p,q}, u\rangle )\) to be a Gaussian PDF with reference direction \(\hat{v}_{p,q}\). We represent the positive and negative hemispheres of the WM AFODF using two independent even-order SH bases. The odd-order SH basis typically captures only noise and is therefore not included in the representation [10]. More specifically, the AFODF can be written as

$$\begin{aligned} F_{p}(u)= \begin{bmatrix} \mathbf {Y}^{+}(u\in \mathbb {S}_{+}^2)&0\\ 0&\mathbf {Y}^{-}(u\in \mathbb {S}_{-}^2) \end{bmatrix} \begin{bmatrix} \mathbf {X}_{\text {WM}}^{+}(p)\\ \mathbf {X}_{\text {WM}}^{-}(p)\\ \end{bmatrix}, \end{aligned}$$
(3)

where \(\mathbf {Y}^{+}(u\in \mathbb {S}_{+}^2)\) and \(\mathbf {Y}^{-}(u\in \mathbb {S}_{-}^2)\) are the real symmetric SH bases defined on different hemispheres of \(\mathbb {S}^2\). \(\mathbf {X}_{\text {WM}}^{+}(p)\) and \(\mathbf {X}_{\text {WM}}^{-}(p)\) are the corresponding SH coefficients.

2.2 Global Estimation Framework

We solve the AFODFs of a set of voxels \(\mathbb {P}=\{p_{1},p_{2},\ldots ,p_{N}\}\) jointly. We group the signal vectors of the N voxels as columns in matrix \(\mathbf {S}\) and the SH coefficients of the AODFs of these voxels as columns in matrix \(\mathbf {X}\). We assume that three tissue types (WM, GM, and CSF) contribute to the signal. The WM FODF is anisotropic and can be represented using an SH series up to order l. The GM and CSF FODFs are isotropic and can be represented using zeroth order SH terms. With a set of directions \(\mathbb {U}=\{u_1, u_2, \ldots ,u_K\}\), AFODFs of the N voxels are solved simultaneously via

$$\begin{aligned} \hat{\mathbf {X}} = \arg \min \limits _{\mathbf {X}} {\left\| \mathbf {R}\mathbf {X} - \mathbf {S} \right\| }_F^{2} \quad \text {s.t.} \quad \mathbf {A}\mathbf {X} \succeq 0 \quad \text {and}\quad \sum _{p\in \mathbb {P},u\in \mathbb {U}} \phi (p,u) \le \epsilon , \end{aligned}$$
(4)

where

$$\begin{aligned} \mathbf {X} = \begin{bmatrix} \mathbf {X}_{\text {WM}}^{+}(p_1)&~\ldots ~&\mathbf {X}_{\text {WM}}^{+}(p_N)\\ \mathbf {X}_{\text {WM}}^{-}(p_1)&~\ldots ~&\mathbf {X}_{\text {WM}}^{-}(p_N)\\ \mathbf {X}_{\text {GM}}(p_1)&~\ldots ~&\mathbf {X}_{\text {CSF}}(p_N)\\ \mathbf {X}_{\text {CSF}}(p_1)&~\ldots ~&\mathbf {X}_{\text {CSF}}(p_N) \end{bmatrix} \quad \text {and} \quad \mathbf {R} = \left[ {\mathbf {R}_{\text {WM}}^{+},\mathbf {R}_{\text {WM}}^{-},\mathbf {R}_{\text {GM}},\mathbf {R}_{\text {CSF}} }\right] . \end{aligned}$$
(5)

Matrix \(\mathbf {R}\) maps the AFODF coefficients to the DW signal by means of spherical convolution. Matrix \(\mathbf {A}\) maps the AFODF coefficients to the AFODF amplitudes and the constraint \(\mathbf {A}\mathbf {X} \succeq 0\) imposes AFODF non-negativity [6]. Function \(\phi (\cdot )\) is as defined in (2), but is computed only for the WM portion of the AFODF.

2.3 Optimization

The constrained linear least-squares problem can be cast as a general strictly convex quadratic programming (QP) problem:

$$\begin{aligned} \begin{aligned} \hat{\mathbf {X}} = \arg \min \limits _{\mathbf {X}} \left( \text {trace} \left[ \frac{1}{2}\mathbf {X}^{\top } \mathbf {H} \mathbf {X} + \mathbf {Q}^{\top } \mathbf {X}\right] \right) ~\\ \text {s.t.}~\mathbf {A}\mathbf {X} \succeq 0~\text {and}~\sum _{p\in \mathbb {P},u\in \mathbb {U}} \phi (p,u) \le \epsilon , \end{aligned} \end{aligned}$$
(6)

with \(\mathbf {H} =\mathbf {R}^{\top } \mathbf {R}\) and \(\mathbf {Q}=-\mathbf {R}^{\top } \mathbf {S}\). \(\hat{\mathbf {X}}\) is obtained via convex optimization using CVXFootnote 1 with MOSEKFootnote 2.

Fig. 1.
figure 1

(a) FODFs and (b) AFODFs with close-up views shown for gyral blades.

Full size image

2.4 Materials and Implementation Details

A DMRI dataset (Subject ID: 105923) from the Human Connectome Project (HCP) [11] was used to validate our method. The dataset has an isotropic spatial resolution of 1.25 mm, with 3 b-values (\(b=1000,2000,3000\,\text {s}/\text {mm}^{2}\)), a total of 270 gradient directions (90 per shell), and 18 non-diffusion-weighted images. Cortical and sub-cortical parcellation was performed on the T1-weighted MR image using FreeSurfer. The cortical GM map generated by FSL using the T1-weighted MR image was used to define tractography seed voxels in the cortex.

SHs up to order 8, amounting to 45 coefficients, are used to represent the positive/negative hemispheres of the AFODF. The AFODF non-negativity and fiber continuity constraints are enforced on 724 uniformly distributed orientations. The response function for each tissue type is estimated for each shell with the help of the tissue segmentation map generated via FSL using the T1-weighted image.

Whole brain tractography was performed using deterministic and probabilistic algorithms [12] using the peak directions of the AFODFs and FODFs. Tracking was performed with the following parameters: 3 tracts per voxel in the cortical GM, 0.5 voxel step size, \(60^{\circ }\) maximum turning angle for deterministic tracking and \(80^{\circ }\) for probabilistic tracking. Tracking was terminated when the fractional anisotropy (FA) value is below 0.1. Streamlines shorter than 10 mm were removed.

Table 1. Valid streamlines.
Full size table

3 Experimental Results

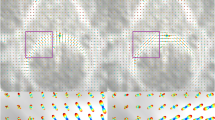
Figure 1 shows the differences between FODFs and AFODFs. We show the close-up views of gyral blades where fiber pathways exhibit high curvature. It can be observed that the AFODFs reflect the bending and branching characteristics of cortical WM pathways. The asymmetry of the AFODFs becomes more apparent for voxels nearer the cortex.

Fig. 2.
figure 2

Tractography using FODFs and AFODFs. The asterisks (‘\(\star \)’) indicate removal of invalid streamlines.

Full size image
Fig. 3.
figure 3

Connectivity between the 164 cortical regions of the Destrieux Atlas [13].

Full size image

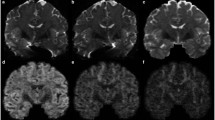
Figure 2 shows the outcomes of deterministic (columns 1 & 2) and probabilistic (columns 3 & 4) tractography. We also show results after removing invalid fiber streamlines that do not terminate in the cortex (columns 2 & 4). Even though tractography was performed for FODFs and AFODFs using the same number of seeds, AFODFs result in a significantly greater amount of streamlines, even after the removal of invalid streamlines. FODFs, on the other hand, result in a larger fraction of invalid streamlines. Quantitative results in Table 1 confirm this observation, suggesting improvements in tractography across WM-GM boundaries. It can also be observed that AFODFs give a larger amount of streamlines entering the sulcal walls. This increases cortical coverage and reduces gyral bias.

Figure 3 shows the connectivity between 164 regions identified by cortical parcellation [13]. The number of streamlines connecting two regions was recorded and a connectivity matrix was then constructed based on normalized streamlines counts. Normalization was performed by pre- and post-multiplication of the connectivity matrix (\(\mathbf {C}\)) with degree matrix (\(\mathbf {D}\)) raised to the power of \(-1/2\), i.e., \(\mathbf {D}^{-\frac{1}{2}}\mathbf {C}\mathbf {D}^{-\frac{1}{2}}\). All connections with normalized counts greater than 0.1 are shown. Self-connections are removed. The results again confirm that AFODFs yield better cortico-cortical connectivity.

4 Conclusion

We have presented a multi-tissue global estimation framework for AFODFs and have demonstrated that AFODFs can be used to mitigate gyral bias in cortical tractography. Our method extends multi-shell multi-tissue CSD by imposing fiber continuity across voxels to resolve orientation asymmetry. We have shown through an HCP dataset that our method resolves realistic sub-voxel fiber configurations and improves deterministic and probabilistic tractography.