Multimodal Fusion of Brain Networks with Longitudinal Couplings

Abstract

In recent years, brain network analysis has attracted considerable interests in the field of neuroimaging analysis. It plays a vital role in understanding biologically fundamental mechanisms of human brains. As the upward trend of multi-source in neuroimaging data collection, effective learning from the different types of data sources, e.g. multimodal and longitudinal data, is much in demand. In this paper, we propose a general coupling framework, the multimodal neuroimaging network fusion with longitudinal couplings (MMLC), to learn the latent representations of brain networks. Specifically, we jointly factorize multimodal networks, assuming a linear relationship to couple network variance across time. Experimental results on two large datasets demonstrate the effectiveness of the proposed framework. The new approach integrates information from longitudinal, multimodal neuroimaging data and boosts statistical power to predict psychometric evaluation measures.

1 Introduction

It is widely accepted that brain has one of the most complex networks known to man. One of the modern approaches in neuroscience is considering the brain regional interactions as a graph network, referred to as brain connectome or brain network [7]. By learning network properties, researchers could draw a broad picture about how the brain controls and regulates information through the orderly transfer of neural signals within brain regions [9]. However, effectively learning features from few noisy brain networks is difficult. It is a common belief that the exploitation of auxiliary and complementary information from the multimodal and longitudinal data would be highly beneficial to improve the effectiveness of brain network analysis.

In practice, brain networks can be analyzed from two perspectives, i.e., multimodal and longitudinal. For multimodal data, functional magnetic resonance imaging (fMRI) and diffusion tensor imaging (DTI) are the most widely used modalities which could yield complementary information of brain networks. Several studies proposed the linear [1] or non-linear [10] multimodal integration approaches for brain network analysis, which significantly improve the detection power of brain structural or mental changes. On the other hand, the longitudinal analysis of brain network portrays progressive changes in brain functional activities or anatomical architectures. For example, as a supplement to baseline analysis, the longitudinal study of age-related changes in the topological organization of structural brain networks effectively explored new patterns of normal aging [15]. It worth noting that the multimodal and longitudinal studies are also inherently related. However, existing works on brain networks usually only consider one perspective of brain networks. It remains a major challenge to achieve multilevel fusion of neuroimages by exploiting these two different types of brain networks.

In this paper, we aim to empower the longitudinal multimodal neuroimaging data fusion with brain network representation learning. We develop a theoretical model (MMLC) which achieves multimodal and longitudinal coupling simultaneously. It bases on two assumptions: (1) both functional and structural networks reflect the regional interactions inside the brain. Thus they should share a similar basis in network topology; (2) the longitudinal changes should relate to the previous as well as the next brain stages. To the best of our knowledge, it is the first work that fuses multimodal and longitudinal brain networks simultaneously. We expect such data fusion model will significantly improve the statistical power of brain network analysis.

2 Brian Network Representation Learning

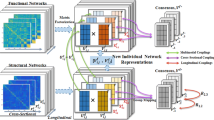
Our brain network fusion framework is presented in Fig. 1, which consists of three coupling components: cross-sectional, multimodal and longitudinal couplings.

Fig. 1.

The proposed MMLC framework. Three levels of information couplings are considered: the cross-sectional coupling (Population), the longitudinal coupling (Multi-scan) and the multimodal coupling (Multi-modality).

2.1 Modeling Cross-Sectional Coupling

It is natural to couple subjects in a population to achieve the individual and group properties. In the cross-sectional coupling, we use the consensus matrix to model group properties. We defined a graph $g=(V,X)$ for the individual brain network, where V is the set of all n brain regions and X is the connectivity matrix which records the connectivity strength between pairs of the regions. For each subject, we have two connectivity matrices, $X^f$ and $X^d$, for functional and structural network respectively. For the whole dataset, suppose we have N subjects and each subject was scanned T times, we have a set of functional and structural connectivity matrices, $\{X_{i,j}^f, X_{i,j}^d |i=1,...,N, j=1,...,T\}$. We conduct network embedding with matrix factorization to map the graph data into a lower dimensional latent space. $X_{i,j}\approx U_{i,j}V_{i,j}^T$ and $V_{i,j}^T\in \mathbb {R}^{N\times P}$ will be the new representation of network in the latent P-dimensional space. To look for the consistent patterns among a population of subjects, we adopt the concept of consensus matrix. If subjects are from the same group, it is natural to hypothesize that it has the similar representations in all graph matrix but only differ on new basis matrix ($U_{i,\cdot }$). Hence, $V_{i,\cdot }$ should be the target to measure disagreement of the network patterns. Here, we introduce a new variable $V^*\in \mathbb {R}^{N\times P}$ named the consensus matrix of $V_{i,\cdot }$ and the following loss function to couple the network representations within a group of items, $\sum _{i=1}^N\parallel V_{i,\cdot }-V^*\parallel ^2_F$. Note that all $V_{i,\cdot }$ are at the same scale because entries of all the original network matrix $X_{i,\cdot }$ locate within the range of $[-1,1]$. Even though the general factorization problem might exist multiple solutions due to the uncertainty of basis matrix, the inter-subjects coupling problem described as below is solvable with the added consensus matrix term and assumption that $X_i$ is within the same range.

$$\begin{aligned} \min _{U_{i,\cdot };V_{i,\cdot }}\sum _{i=1}^N\parallel {X_{i,\cdot }-U_{i,\cdot }V_{i,\cdot }^T}\parallel ^2_F+\lambda \parallel V_{i,\cdot }-V^*\parallel ^2_F. \end{aligned}$$

(1)

2.2 Modeling Multimodal Coupling

The structural network builds the anatomical foundations of the functional network. Therefore, there should be the topological similarities between them. Here, we share the basis matrix in Eq. 1 across modality. In this study, we chose a newly proposed brain atlas which has 246 brain regions and reflects both functional and structural connectivity patterns [4]. Ideally, the brain network created from fine-grained atlas contains more details of the regional interaction [16]. After matrix factorization, we get two new network representations for each subject i as $V^f_{i,\cdot }$ and $V^d_{i,\cdot }$ with the corresponding basis matrices $U^f_{i,\cdot }$ and $U^d_{i,\cdot }$. We hypothesize that there are quite significant similarities between those two kinds of networks that can be interpreted with specific presentations in latent space. In other words, given a subject i, the functional and structural networks share the same basis matrix $U^f_{i,\cdot }=U^d_{i,\cdot }=U_{i,\cdot }$. Though the similarities of multimodal brain networks might be deciphered as the linear or non-linear relationships, we only focus on the linear relationship in this study. For future study, we could model the non-linear relationship with the high-order of basis matrix. Eventually, together with the inter-subject coupling model, we propose the multi-modality coupling model as below:

$$\begin{aligned} \begin{aligned} \min _{U_{i,\cdot };V_{i,\cdot }}&\sum _{i=1}^N\parallel {X^f_{i,\cdot }-U_{i,\cdot }(V^f_{i,\cdot })^T}\parallel ^2_F+\alpha \parallel {X^d_{i,\cdot }-U_{i,\cdot }(V^d_{i,\cdot })^T}\parallel ^2_F \\&+\lambda _1\parallel V^f_{i,\cdot }-V^{f*}\parallel ^2_F+\lambda _1\parallel V^d_{i,\cdot }-V^{d*}\parallel ^2_F. \end{aligned} \end{aligned}$$

(2)

2.3 Modeling Longitudinal Coupling

In the longitudinal coupling, we track how the brain evolves over time. We model the smooth variation of brain networks as a Procrustes problem which maps the consensus matrix to a same effect space [8]. First, we improve the model by adding an orthogonality constraint $(V^{d*}_{\cdot })^TV^{d*}_{\cdot }=I$ to the consensus matrix in the structural network. The matrix factorization with orthogonality constraint plays a similar role as the clustering [12] which is consistent with the subgraph organization in human brain networks. After adding the orthogonality constraint in every time point, we further model the relationships between each consecutive pairs of consensus matrix. Suppose we have two consensus matrixes $V^{d*}_{j}$ and $V^{d*}_{j+1}$ from two consecutive time points j and $j+1$. Due to the relative stability of structural network within subject, we expect that $V^{d*}_{j}$ shares a rotation relationship with $V^{d*}_{j+1}$, i.e. $V^{d*}_{j}=R_{j,j+1}V^{d*}_{j+1}$. $R_{j,j+1}\in \mathbb {R}^{n\times n}$ is a rotation matrix thus $det(R_{j,j+1})=1$ and $R_{j+1,j}=R_{j,j+1}^{-1}=R_{j,j+1}^T$. As $(V^{d*}_{j})^TV^{d*}_{j}=I$ is satisfied for all j, taking the rotation relationship into such orthogonality, we could construct a new symmetric matrix, $\tilde{M}_{j+1,j}=R_{j+1,j}V^{d*}_{j+1}(V^{d*}_{j+1})^TR_{j+1,j}^T$, that $(V^{d*}_{j})^T\tilde{M}_{j+1,j}V^{d*}_{j}=I$. Then we merge the consecutive relations from time j to $j+1$ of $V^{d*}_{j}$ into a single time variable j as $M_{j} = (\tilde{M}_{j-1,j}+\tilde{M}_{j+1,j})/2$. The constraint, $(V^{d*}_{j})^T\tilde{M}_{j+1,j}V^{d*}_{j}=I$, is called the generalized Stiefel constraint [2] with the mass matrix $M_{i,j}$. In this paper, we applied an optimization algorithm involves the Stiefel manifold based on the Cayley transform for preserving the constraints [6].

2.4 The Proposed Model - MMLC

Now let’s reformulate the problem for all N subjects and T time points. The multimodal brain network fusion with longitudinal coupling framework is to solve the problem of minimizing the following objective function, L, with the corresponding constraint:

$$\begin{aligned} \begin{aligned} \min _{\begin{array}{c} U,V^f,V^d, \\ V^{f*},V^{d*} \end{array}}&\sum _{i=1}^N\sum _{j=1}^T\parallel {X^f_{i,j}-U_{i,j}(V^f_{i,j})^T}\parallel ^2_F +\alpha \parallel {X^d_{i,j}-U_{i,j}(V^d_{i,j})^T}\parallel ^2_F \\&+\lambda _1\parallel V^f_{i,j}-V^{f*}_{j}\parallel ^2_F+\lambda _1\parallel V^d_{i,j}-V^{d*}_{j}\parallel ^2_F +\lambda _2G \\ s.t. \;&(V^{d*}_{j})^TM_{i,j}V^{d*}_{j}=I \end{aligned} \end{aligned}$$

(3)

where $G=\;\parallel U_{i,j}\parallel ^2_F+\parallel V^f_{i,j}\parallel ^2_F+\parallel V^d_{i,j}\parallel ^2_F+\parallel V^{f*}_{j}\parallel ^2_F+\parallel V^{d*}_{j}\parallel ^2_F$ is the regularization term to prevent overfitting.

3 An Optimization Framework for MMLC

The problem proposed in Eq. 3 is a non-convex problem which is difficult to optimize directly. To estimate the optimal, we propose an iterative update procedure together with a Stochastic block coordinate descent algorithm.

Fixing $\varvec{V^{f*}_{j}}$ and $\varvec{V^{d*}_{j}}$, minimize L over $\varvec{U_{i,j}, V^f_{i,j}}$ and $\varvec{V^d_{i,j}}$. For brevity in this subsection, we use $U, V^f, V^d, V^{f*}$ and $V^{d*}$ to represent $U_{i,j}, V^f_{i,j}, V^d_{i,j}, V^{f*}_{j}$ and $V^{d*}_{j}$. First, we fix $V^f$ and $V^d$ to update U. For a given subject i and time point j, we could take the derivative of L with respect to U.

$$\begin{aligned} \begin{aligned} \frac{\partial L}{\partial U}=&2(U(V^f)^TV^f-X^fV^f)+2\alpha (U(V^d)^TV^d-X^dV^d))+\lambda _2G^{'}(U). \end{aligned} \end{aligned}$$

(4)

Here, $G^{'}(U)$ is the derivative of U with respect to U. Given a step size l, we update U as $U_{new}=U_{pre}-l*\frac{\partial L_1}{\partial U_{pre}}$. Then, we fix $V^d$ and U to update $V^f$. The gradient of L with respect to $V^f$ is:

$$\begin{aligned} \begin{aligned} \frac{\partial L}{\partial V^f}=&2(V^fU^TU-X^fU)+2\lambda _1(V^f-V^{f*})+\lambda _2G^{'}(V^f). \end{aligned} \end{aligned}$$

(5)

Similarly, we update $V^d$ with the same procedure as $V^f$,

$$\begin{aligned} \begin{aligned} \frac{\partial L}{\partial V^d}=&2\alpha (V^d(U)^TU-X^dU) +2\lambda _1(V^d-V^{d*})+\lambda _2G^{'}(V^d). \end{aligned} \end{aligned}$$

(6)

Fixing $\varvec{U_{i,j}, V^f_{i,j}}$ and $\varvec{V^d_{i,j}}$, Minimize L over $\varvec{V^{f*}_{j}}$ and $\varvec{V^{d*}_{j}}$. For brevity, we use $V^f_i, V^d_i, V^{f*}$ and $V^{d*}$ to represent $V^f_{i,j}, V^d_{i,j}, V^{f*}_{j}$ and $V^{d*}_{j}$. We observe that for each time j, the framework will generate a group-wise $V^{f*}_{j}$ and $V^{d*}_{j}$. After updating all individual $U_i$, $V^f_i$ and $V^d_i$, we could take the derivative of L with respect to $V^{f*}$.

$$\begin{aligned} \begin{aligned} \frac{\partial L}{\partial V^{f*}}=2\lambda _1\sum _{i=1}^N(V^{f*}-V^f_i)+\lambda _2G^{'}(V^{f*}). \end{aligned} \end{aligned}$$

(7)

For $V^{d*}$, an equality constraint $(V^{d*})^TMV^{d*}=I$ will regulate the gradient direction of L with respect to $V^{d*}$, which makes the solution difficult. Instead of directly finding an optimal direction with gradient descent on the surface described by original object function, we construct the descent curves on the constraint-based Stiefel manifold [6]. Specifically, $V^{d*}$ will be divided into two submatrixes $V^{d*}=[V^{d*}_1; V^{d*}_2]$, where $V^{d*}_1\in \mathbb {R}^{s\times p}$ is the free variable to be solved and $V^{d*}_2\in \mathbb {R}^{(n-s)\times p}$ is the fixed variable treated as constants. Then we rearrange the constraint as:

$$\begin{aligned} \begin{bmatrix} V^{d*}_1\\ V^{d*}_2 \end{bmatrix}^T\begin{bmatrix} M_{11}&M_{12}\\ M_{12}^T&M_{22} \end{bmatrix}\begin{bmatrix} V^{d*}_1\\ V^{d*}_2 \end{bmatrix}=I. \end{aligned}$$

(8)

It is easy to conclude that $M_{11}$ is a full rank positive definite matrix. Then a descent curve based on the previous $V^{d*}$ will be constructed and it starts at the point $P_s=V^{d*}_1\,+\,M_{11}^{-\frac{1}{2}}M_{12}V^{d*}_2$ which is the initial point for the line search on the generalized Stiefel manifold. Given the descending gradient $-L^{'}(P)=-\frac{\partial L}{\partial V^{d*}}\,\circ \,\frac{\partial V^{d*}}{\partial P}$ at point P, we further project $-L^{'}(P)$ onto the tangent space of the Stiefel manifold by constructing a skew-symmetric matrix $A=L^{'}(P)P_s^T-P_sL^{'}(P)^T$. This will lead to a curve function $Y(\tau )$ by the Crank-Nicolson-like design as in paper [14].

$$\begin{aligned} Y(\tau )=(I+\frac{\tau }{2}AM_{11})^{-1}(I-\frac{\tau }{2}AM_{11})P_s. \end{aligned}$$

(9)

The above function gives a linear search procedure of updating point P by $P_{new}=Y(\tau )$ for small $\tau$ which results sufficient decrease in $L_2$. Finally, the next feasible $V^{d*}_{new}$ will be given as:

$$\begin{aligned} V^{d*}_{new}(P)= \begin{bmatrix} P-M_{11}^{-\frac{1}{2}}M_{12}V^{d*}_2\\ V^{d*}_2 \end{bmatrix}. \end{aligned}$$

(10)

4 Experiment

4.1 Experimental Settings and Baseline Methods

In this paper, we use two datasets to test the effectiveness of the proposed method in predicting anxiety and depression scores, respectively. They are all from the SLIM Repository (Southwest University Longitudinal Imaging Multimodal Brain Data)¹. Dataset1 contains 105 healthy subjects and the trait anxiety score (TAIs) based on the State Trait Anxiety Inventory (STAI) was set as the predicted variables. Dataset2 includes 77 subjects with the assessment of ATQ (Automatic Thoughts Questionnaire) self-report measures which reflect mental states associated with depression and was the predicted variables in this trial. All subjects in two datasets are right-handed college students with the close age gaps and similar education level. We preprocessed fMRI data by using AFNI software² and using FSL³ for DTI data. Then we construct the functional and structural networks with brain connectivity toolbox⁴. The gap between each pair of consecutive imaging scans is 1.5 years and 3 scans per person are collected. We aim to predict the score of anxiety and depression, which is a regression task. To evaluate the regression performance, we adopt the two wildly used evaluation metrics, i.e., root mean square error (RMSE) and mean absolute error (MAE).

We compare the performance of MMLC with representative and state-of-the-art brain network representation learning algorithms as follows: MFCSMC: the collective matrix factorization [13] on multiple modalities with the cross-sectional coupling; EigLC [5]: a state-of-the-art method which models the longitudinal coupling on a single modality, i.e., structural networks; sMFLC: a variant of EigLC by removing the terms concerning functional networks in our model and remaining the matrix factorization (MF) with longitudinal coupling of structural networks; MFCSLC: MF with cross-sectional and Longitudinal coupling without sharing the basis matrix U. It is a variant of MMLC. Subject i will obtain his new feature set $[V^f_{i,j},V^d_{i,j}]$ at time point j as the new representation of his original network graphs. We feed the vectorized features and the corresponding scores into a linear regression model for training by using LIBSVM toolbox [3]. In this experiment, each time we randomly pick 70% subjects as the training set and test on the rest. We repeat this process 30 times and the average performance and standard deviation are reported.

4.2 Results

We present the regression performance of our proposed model as opposite to other compared methods in Table 1. We set $\alpha =1, \lambda _1=20$ for Dataset 1 and $\alpha =5, \lambda _1=20$ for Dataset 2 according to the cross validation and empirically chose $\lambda _2$ to be 0.1 and dimension of the new feature space $P=10$. From Table 1, we see that our proposed model outperforms other methods in two datasets. For example, sMFLC, the single modality version of our proposed model with longitudinal coupling have better performance than EigLC significantly. The difference of regression performance between the full coupling and partial coupling of multimodal or longitudinal fusions is small but significant. For example, in Dataset 2, the result of the partial coupling of brain networks in the multimodal fusion (MFCSMC) has the higher value of MAE ($p<0.0006$, two-sample t-test) and RMSE ($p<0.153$) than MMLC. Besides, MMLC outperforms MFCSLC which contains only longitudinal coupling in two datasets. In all, MMLC has the smallest MAE and RMSE values together with the relatively low variance compared with other testing methods in our experiments.

The proposed framework has two important parameters, i.e., $\alpha$ controlling the contribution of multimodal and $\lambda _1$ controlling cross-sectional coupling. In this section, we evaluate the affects of $\alpha$ and $\lambda _1$ on MMLC. Specifically, we vary $\alpha$ as $\{0.5,1,5,10,20\}$ and $\lambda _1$ as $\{1,10,20,30,40\}$. The results in terms of MAE and RMSE are shown in Figs. 2 and 3. From the figure, we observe that: (i) In Dataset 1, both MAE and RMSE value reach the relatively lowest points when $\alpha =1$. Then, there is a tendency that MAE and RMSE increases along with the increase of $\alpha$. In Dataset 2, the variation of MAE and RMSE is more apparent when $\alpha$ increases to a higher value, e.g., $\alpha >10$ and meanwhile the prediction performance has a significant drop. (ii) Moreover, when $\lambda _1=20$, our framework has the relatively best performance in both datasets. In this experiment, we observe the different optimal parameter settings on tasks from two different domains, i.e., anxiety and depression. This is consistent with the previous discovery in brain networks that the distinct roles of functional and structural connectivities shift in different cognition tasks [11].

Table 1. Regression performance on anxiety and depression datasets

Fig. 2.

Performance on Dataset 1 (anxiety)

Fig. 3.

Performance on Dataset 2 (depression)

5 Conclusion and Future Works

This paper describes a novel network fusion framework which simultaneously considers multiple levels of information such as relationships between brain functional and structural organizations and longitudinal brain development. We test our proposed framework with two large cohorts and experimental results demonstrate the effectiveness of the generated network representations for prediction of cognitive status. There are several interesting directions that are warranted for further investigation. For example, in the future, we could add the non-linear relationship of multimodal networks to our framework or investigate subnetwork patterns that can be derived from the learned network representations.