1 Introduction

The two lines of research addressed in this study, one focusing on generalisation in an algebraic thinking context in primary education and the other on mathematics learning in autism spectrum disorder (ASD) students, form part of two projects presently underway in Spain.

According to some studies, primary school (6- to 12-year-old) students are able to think algebraically, and classroom activities designed to develop that capacity are highly beneficial (Blanton & Kaput, 2004; Brizuela & Martínez, 2012). Authors such as Morales et al. (2018) highlight the importance of and need for studies with students as they perform mathematical tasks, especially problem solving, in the context of functions.

More and more often, and in a number of countries, children with ASD are being enrolled in mainstream schools. Some of the deficits that are characteristic of the disorder, such as deficits in executive functions or verbal comprehension, may interfere with learning mathematical concepts (e.g., Chen et al., 2019). As a consequence, nearly a quarter of school-aged students with ASD have a learning disability in mathematics, compared with 5% to 8% of all school-age children (Mayes & Calhoun, 2003). Furthermore, in middle school, mathematics become more abstract, emphasising abstract reasoning and problem solving (Ministerio de Educación, Cultura y Deporte, 2014; NCTM, 2000), which can be a weakness for children with ASD (Mayes & Calhoun, 2003).

Given that one outcome of the traits characteristic of ASD is that students with the disorder may find it difficult to assimilate the school curriculum, education professionals must understand this community’s strengths and weaknesses in all academic areas. Particular interest has been expressed in gaining greater insight into mathematics learning among ASD students (Barnett & Cleary, 2019; Root & Browder, 2019). Nonetheless, algebraic thinking in students with this disorder has seldom been addressed in any depth. In the present study, we aspire to help narrow the existing knowledge gap. The study focuses on the strategies deployed by ASD students to perform a task involving a functional relationship, with a view to identifying their difficulties and strengths when engaging in algebraic thinking.

2 Algebraic thinking, functional thinking, generalisation and representation

Interest in introducing and furthering algebraic thinking in primary school classroom mathematics first arose in the 90s (Lins & Kaput, 2004). The result of those endeavours, early algebra, endorses the introduction of algebraic thinking in pre-secondary education (Blanton et al., 2015). That idea continues to arouse interest in mathematics education, as attested to by professional fora on the subject. The present ZDM monograph is one example of this focus of interest.

Although algebraic thinking is a ‘mature’ domain within mathematics education research (e.g., Kieran, 2006), the term may be defined differently. Kaput is one of the most influential authors in the area of early algebra. In 2008 he contended that algebraic thinking, along with talking about algebra and performing algebraic tasks, forms part of mathematical content. For Blanton and Kaput (2004), algebraic thinking entails generalising mathematical relationships. According to Radford (2010), algebraic thinking has the following components: (a) unknowns, variables and parameters as basic objects, (b) operations involving those basic objects and (c) the specific way such basic objects are referred to. Early algebra involves activities that can be conducted by students with no need to use letters or algebraic symbols, such as the following: analysing relationships between quantities, generalising, solving problems, modelling, explaining, proving and predicting (Kieran, 2004).

Functional thinking is a component of algebraic thinking, for functions further the understanding of many real-life problems and serve as a basis for predicting real-life events (Blanton, 2008). According to Blanton, it is “a process of building, describing and thinking with and about functions” (p. 30). Introducing primary school children to functional thinking fosters their ability to generalise, explain and reason with mathematical relationships (Blanton et al., 2015). It may also facilitate their understanding of functions when formally addressed in secondary school (Doorman & Drijvers, 2011).

Research on functional thinking focuses, among other aspects, on functional relationships, generalisation, errors and difficulties, strategies, and representation. Specific attention has been paid to generalisation as a core aspect of algebraic thinking (Kaput, 2008). Generalisation is an essential component in mathematics (Mason et al., 1985), but “the grounds for generalisation differ considerably in mathematics and early mathematics education” (Carraher et al., 2008, p. 3). In that vein, we consider the importance of moving from the particular to the general, but also how students ‘see’ regularity and express it through different representations in different ways. The process of generalisation here is as important as the result. In line with Blanton et al. (2019), we assume that generalising and representing generalisations are the essence of generalisation. We find evidence of students using a general idea and applying it to other particular terms when they have not expressed the generalisation (Pinto et al., 2021). In this research, the authors described the work of 8- to 11-year-olds in a context of generalisation, when solving a problem involving the function y = 2x + 6. All the fifth-year (11-year-old) students generalised the relationship, primarily using natural language.

As functional thinking involves functions, generalisation here applies to the relationships concerning variables of the functions involved. According to Blanton and Kaput (2011), functional thinking involves the “construction and generalisation of patterns and relationships, using a diversity of representations and treating generalised relationships, or functions, as the result of useful mathematical objects” (pp. 6–7).

One of the foremost classroom exercises to foster algebraic thinking described by Kaput (2008) is generalisation; it is instrumental to functional thinking. It consists in moving from specifics to general understanding. The literature on functional thinking distinguishes between (a) recursive patterns and (b) functional relationships. In the latter the focus is on correspondence and covariation. Some studies have shown how to move from recurrence to functional strategies (e.g., Blanton et al., 2015; Cañadas et al., 2016). Blanton et al. (2015) described the functional thinking exhibited by 6- and 7-year-olds. The eight levels of functional thinking they identified include the following: (a) pre-structural, (b) recursive-particular, (c) recursive-general, (d) functional-particular, (e) primitive functional-general, (f) emergent functional-general, (g) condensed functional-general and (h) functions as object relationships. Reaching the eighth level entails perceiving the generality involved. We provide some examples of these levels in the results section.

Representation is one of the core practices considered by Kaput (2008) for promoting algebraic thinking in classrooms. Representations are sets of signs and rules that are conditioned by mathematics in general and by the specific mathematical concept in particular (Goldin & Shteingold, 2001). They are a way to describe and analyse how students perceive and express the structures and relationships embedded in a given problem, which helps to structure and expand students’ thinking (Brizuela & Earnest, 2008). Among Brizuela and Earnest’s (2008) aims are to investigate how students represent the mathematical notions involved, which representations they give priority to, how they interpret mathematical representations, how they combine representations, and how they switch from one to another. In functional thinking studies, representations are addressed as a cross-cutting aspect. In our study, we considered this cross-cutting feature, which contributes to describing the process of generalisation performed by students.

In research, functional thinking has been approached from different perspectives to introduce algebraic notions in primary education. Generalisation, involved in most of these studies, is a key element in functional thinking and is one of the focuses of this paper. In particular, we focus on the steps of the functional approach put forward by Blanton et al. (2015) to describe the process towards generalisation.

3 Strategies in the functional approach to problem solving

Problem solving, associated with functional thinking, is the core issue addressed in this study. A number of authors have discussed the heuristics and strategies called into play when explaining how tasks are performed. Some researchers have stressed the need to explore the strategies used by students to solve problems in functional contexts (e.g., Amit & Neria, 2008; Moss & Beatty, 2006).

The literature describes the strategies deployed by mainstream education students (6- to 12-year-olds) when generalising in functional contexts. In most of these studies, we observe strategies linked to (a) representations, (b) arithmetical aspects (operating or counting strategies) (e.g., Blanton & Kaput, 2004; Cañadas & Fuentes, 2015; Morales et al., 2018) or (c) functional relationships (e.g., Cañadas et al., 2016). In some cases, researchers worked on two or more of these aspects together with strategies. In what follows, we detail some of these aspects.

Representations were introduced in the previous section. This focus of interest can also be combined with others, such as strategies. For example, the paper by Cañadas and Fuentes (2015) about arithmetical aspects and representations distinguished among the following strategies: (a) counting on the drawings, (b) bald answering, (c) associating grouped elements, (d) changing the number in the relationship and (e) other (strategies not covered in the previous answers). First graders (6- to 7-year-old students) mainly tended to answer pictorially, though also numerically or verbally. The exception to that rule was the item on generalisation, where verbal representation prevailed, in combination in some cases with other types of representation. Some of the studies also examined the transition between two of the aforementioned approaches. For example, Ramírez et al. (2020) focused on the transition from arithmetic to functional strategies. They studied 9- to 10-year-old students’ use of functional strategies and their ability to represent generalisation in functions. The authors distinguished the following strategies: (a) functional, when students identified the quantities involved and their relationship, recognising covariation or correspondence; (b) arithmetic, when students used elementary arithmetic operations without realising any relationship between data and solution; and (c) manipulative or visual strategies, when students did not use arithmetic operations but resorted to counting, drawing or using manipulatives.

Some previous studies identified differences in students’ strategies depending on factors such as student age (Blanton & Kaput, 2004; Pinto & Cañadas, 2021) or the kind of questions posed (Cañadas et al., 2016; Morales et al., 2018). Blanton and Kaput (2004) described the following results: pre-schoolers adopted counting and additive approaches in the main; first- and second-year students adopted multiplicative strategies; and third- to fifth-year pupils adopted the same strategies but expressed results both verbally and symbolically when solving a problem involving the function f(x) = 3x. Morales et al. (2018) described the strategies deployed by a group of six-year-olds. They used operating (e.g., number facts) rather than counting strategies (e.g., minimum addend strategy), irrespective of the quantities set out in the exercises. Larger numbers (up to 100) in some of the questions did not prevent the students from operating with them. Cañadas et al. (2016) found that the students used recursive strategies when small numbers (1–20) were involved in the questions, but with larger quantities they used the functional approach.

We identified some studies focusing on the strategies used with mainstream students in primary education (6–12 years old) in a functional context. We did not find evidence of the problem-solving strategies employed by students with learning difficulties in the functional context. Hence, we started from the studies cited above as a basis for exploring the work done by students with ASD.

4 Autism spectrum disorder

As we mentioned above, different factors can influence the process of generalisation. Some of these factors may be psychological in nature. Accordingly, we now discuss autism spectrum disorder (ASD), because the participants of this research are children with ASD.

ASD is a neurodevelopmental disorder that appears in young children and persists throughout the life cycle. According to the Diagnostic and Statistical Manual of Mental Disorders-5 DSM-V (American Psychiatric Association APA, 2013), the symptoms essentially include the following: (a) persistent deficits in social-emotional communication, and (b) restrictive, repetitive patterns of behaviour, interests or activities. People with ASD tend to follow consistent routines and often interpret figurative language literally (Happé, 1993). They may also exhibit inadequacies in inferring other people’s mental state (theory of mind), deficiencies in executive functions (such as planning) or a limited attention span (Ozonoff & Schetter, 2007). However, these students may also benefit from a type of visual thinking characteristic of the disorder, which, as Grandin (1995) describes it, is the capacity to think and reason through images and visual systems. As such thinking may prove useful for certain tasks, educators should identify this and other aptitudes to capitalise on students’ strengths (Ozonoff & Schetter, 2007).

Pupils with this disorder are being enrolled more and more frequently in mainstream schools with typically developing classmates and are expected to master basic curricular content, mathematics included (Barnett & Cleary, 2019). To address the issues arising in that regard, a few studies on mathematics learning in the ASD community have been undertaken in recent years. Most of the research focuses on problem solving and learning arithmetic operations (Gevarter et al., 2016; Polo-Blanco et al., in press). Research on the subject has found that ASD students may use rudimentary strategies such as counting to solve multiplicative problems (Bae et al., 2015; Polo-Blanco et al., 2021). The representations deployed can furnish information on how these pupils, whose language comprehension is often impaired (APA, 2013), understand and solve problems (Gevarter et al., 2016).

5 ASD students’ learning of algebra

Some researchers have explored how algebra is learnt by pupils with special needs. They have focused on secondary education, trying to support the learning process through materials or methods for specific algebraic contents when working with ASD students (e.g., Barnett & Cleary, 2019; Root & Browder, 2019), or on primary students with learning difficulties when working with algebraic relationships in operations (Xin et al., 2011).

No precedents of studies exploring functional thinking in ASD students were found in the literature, except those of Goñi-Cervera et al. (2021) and Polo-Blanco et al. (under review). The former is a conference paper that describes the strategies applied by five primary education ASD students in a generalising task. The authors found the use of modelling, and more specifically drawing, to prevail, irrespective of whether the items involved consecutive or non-consecutive terms. Most of the students did not generalise. Polo-Blanco et al. (under review) identified and described the functional relationships recognised by six primary education ASD students in grades four to six when solving a problem. They identified recurrence, correspondence and covariation as functional relationships. The present work augments these studies by expanding the ASD sample in size (from five and six students, respectively, to 26 students) and age range (covering all six years of primary education) and by focusing on the types of strategies and representations they use, as well as the generalisation they exhibit.

Inasmuch as a growing number of ASD students are enrolling in secondary education (Barnett & Cleary, 2019), and given the ever greater importance attached by the mathematics education research community to introducing algebraic thinking beginning in pre-school, such students must be afforded a sound basis for learning algebra later.

6 Research objectives

In the study discussed in this paper we aimed to identify and describe the strategies exhibited in a context of functional thinking by 26 primary education students diagnosed with ASD when performing a task. We defined two specific objectives, as follows:

  • To describe the strategies and representations used by these students with ASD when solving a problem in a functional context.

  • To describe the generalisations performed by these students.

7 Methodology

We conducted an exploratory and descriptive survey (Yin, 2017) to identify participants’ reasoning in connection with our research questions, namely, to describe the strategies and representations used and the generalisation performed by the participants when solving a task in a functional context.

7.1 Participants

The participants in this study were 26 ASD-diagnosed 6- to 12-year-olds (mean age 9.08 years) without intellectual disability (IQ = 70 or over; mean 89.4), enrolled in first- to sixth-year primary schools. Five were in the first year (S1–S5), one in second (S6), four in third (S7–S10), eight in fourth (S11–S18), two in fifth (S19, S20) and six in sixth (S21–S26). Appendix 1 lists each student’s year of schooling, chronological age and IQ. The participants were enrolled in 19 mainstream schools in 10 towns in Spain and received support from specialist teachers. The type and hours of support these children received varied in keeping with their needs.

The participants were recruited through social networks, the press, associations of disabled or ASD persons, school counselling services and hospital out-patient clinics. The research team participating in the broader research included mathematics education researchers and psychiatrists and psychologists affiliated with hospitals, and autism or disability associations. The psychiatry team, working one-on-one, verified candidates’ compliance with the diagnostic criteria set out in the Diagnostic and Statistical Manual of Mental Disorders (DSM-5, APA, 2013). The psychology team then conducted two or three sessions with each participant to assess the cognitive variables. In a further two or three sessions with mathematics education specialists, performance tests were administered to investigate students’ mathematical problem solving and functional thinking. In this paper we focus on the last of these mathematics sessions, in which the participants were presented with the task described below.

7.2 Instrument

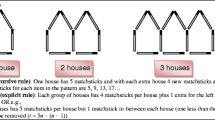
The instrument was a written questionnaire with a task involving the function f(x) = 2x + 2, adapted from Carraher et al. (2008) and taking the type of participants into consideration. The task has been applied in other studies with elementary students across the age range (e.g., Blanton et al., 2015; Cañadas et al., 2016). It was therefore considered appropriate for the participants of the study, since they followed the Spanish elementary curriculum, which states that from first grade students work to “recognise and describe regularities and patterns in numerical, geometric, and functional contexts” (Ministerio de Educación, Cultura y Deporte, 2014, pp. 19, 387).

The adaptation of the task for the ASD students consisted in incorporating visual support representing the context of the task, in view of the fact that good visual processing is prevalent in students with ASD. Manipulatives were provided so that they could use them. The task was also simplified in terms of language, introduced gradually and read aloud to the students. The task was described as depicted in Fig. 1.

Fig. 1
figure 1

Task introduction

Full size image

The items of the task concerned both specific cases and the general term. The cases were classified under one of three headings or terms, as (a) consecutive, (b) non-consecutive, or (c) general.

The questionnaire was used during an individual semi-structured interview, where students were invited to reply in writing or orally. The interviewer (the first author of this paper) introduced the students to the task with one and two tables. She then asked them how many could sit around several larger numbers of tables. We also included an item about generalisation. We present the items in Table 1.

Table 1 Items
Full size table

The interviewer gave them the questionnaire on paper, a pen and a set of interlocking building blocks. She helped them read the problem as needed and encouraged them to solve it. She also asked them to explain their reasoning when answering the questions. The answers were video-recorded and transcribed for subsequent analysis.

7.3 Analysis categories

The information collected consisted in the students’ written answers and oral replies transcribed from the video recordings. We analysed the information using a system of categories based on the authors’ background and research objectives. After a number of revisions and consultation with three experts, we defined the categories ultimately used to analyse the strategies and representations the students applied to solve the problem.

Strategies were classified under the following six categories: (a) non-answering, where students failed to answer orally or in writing, or said they did not know how or did not wish to answer; (b) bald answering, where an answer but no explanation was given; (c) modelling with manipulatives and counting, where the students used the manipulatives at hand (cubes or building blocks) to depict the task posed; (d) modelling with drawing and counting, where they depicted the situation with drawings; (e) counting, where they performed the same actions as in modelling or drawing, but without manipulatives or drawings; and (f) operating, where they added or multiplied orally, in writing or on their fingers.

The types of representation considered for this study, adapted from prior research (Cañadas & Figueiras, 2011; Pinto et al., 2021), included the following: (a) pictorial, where students used visual resources only, with no notation that could be deemed symbolic; (b) manipulative, where they used manipulatives to represent the strategy; (c) verbal, where they used natural language to describe the mathematical ideas and procedures represented; and (d) numerical, where they used algebraic symbols, numbers or operations expressed in mathematical language. Multiple representations, involving two or more types of representation, were also recorded, namely, (e) pictorial-verbal, (f) pictorial-numerical, (g) manipulative-numerical and (h) manipulative-verbal.

To describe the type of generalisation performed by the students, we took into account the following eight levels of generalisation of functional relationships proposed by Blanton et al. (2015): (level 1) pre-structural; (level 2) recursive-particular; (level 3) recursive-general; (level 4) functional-particular; (level 5) primitive functional-general; (level 6) emergent functional-general; (level 7) condensed functional-general and (level 8) ‘functions as object’ relationships. In this study we considered that students generalised if they identified the correct functional relationship at least at a primitive functional-general level (level 5 or higher).

8 Results

The strategies used by students when answering the questionnaire are discussed below, in conjunction with the types of representation identified. A general description is followed by specific examples of students’ replies. Both the written answers and the replies given in the semi-structured interviews were analysed.

Table 2 lists the number of times each strategy was exhibited by the students, organised by item type. The frequency is followed in parentheses by the number of strategies that led to the correct answer. For example, for the item about three tables (x = 3), eight bald answers were observed, three of which were correct.

Table 2 Strategies used
Full size table

In the scant cases where more than one strategy was observed, only the one that led to the student’s reply was recorded. The type of representation applied by students was also analysed. The sub-sections below describe the strategies identified by type of term.

8.1 Strategies in items about consecutive terms

All 26 students answered the items about the consecutive terms x = 3, 4 and 5.

As Table 2 shows, the strategies most frequently used by students to answer items involving consecutive terms were drawing and bald answering. In 20 of the 25 cases where students used drawing as a strategy, the answers were correct. The examples of pictorial representation used with drawing reproduced in Fig. 2 were extracted from the questionnaires answered by S14 (x = 3), S21 (x = 4) and S25 (x = 5).

Fig. 2
figure 2

Examples of drawing strategy for 3, 4 and 5 tables

Full size image

S14 (Fig. 2a) correctly drew three tables when asked to calculate the number of people for x = 3, but showed 12 seats. He drew one person at each end but was inconsistent in the number of seats along each side, drawing one at some tables and two at others. S21 (Fig. 2, centre) gave the right answer to the x = 4 question, drawing four tables and arranging the seating correctly. S25 (Fig. 2, right) drew five tables in her reply to the x = 5 question, then drew in the seating and added in writing (correctly): ‘Twelve people can sit there’.

On three occasions, students combined drawing with other types of representation (multiple representations). S3 used pictorial and numerical representation when replying to the items with x = 4 and x = 5. For x = 4, she drew four tables but no chairs (Fig. 3). Then, using the drawing, she explained that the tables could accommodate eight seats because ‘four plus four makes eight’. The dots in the middle of the tables indicate that the student counted them to ensure the four specified in the item were depicted.

Fig. 3
figure 3

Example of drawing strategy with multiple (pictorial-numerical) representation

Full size image

The 11 students who did not provide an explanation when answering the consecutive term items were deemed to use the bald answering strategy. For instance, when asked, ‘How many people can sit at three tables?’, S10 answered orally, ‘Ten’. When asked, ‘How did you figure that out?’, he replied, ‘Thinking about it’.

Four of the 21 answers found with the second most frequently used strategy, operating, were correct. For instance, S22 replied correctly ‘Eight’ for three tables and then added by way of explanation, ‘There would be two more’. S12 also operated to answer the consecutive items, although incorrectly for x = 3, replying, ‘Ten. Because if there are six at two tables and one at four, if we add a table with four, we get four plus six equals 10’.

The students who used operating as a strategy represented their replies verbally and numerically, although more often the former, with 12 of 21 in all. S23 verbalised the strategy replying orally and correctly for x = 4, ‘Ten. I simply don’t need to draw the tables, there are simply two more’ (meaning two more than the answer to the preceding item). For x = 5, S12 also used verbal representation and answered orally, although incorrectly, ‘Eighteen, because if there are 14 at four tables and four at one, 14 plus 4 is 18’. Here the student was reasoning recursively with respect to the preceding item, adding four seats per table. S9’s and S17’s numerical representations, used in conjunction with operating, are reproduced in Fig. 4. S17 (Fig. 4, left) answered incorrectly for x = 3, as shown in Fig. 4a. For x = 5, the sum given by S9 for x = 5 (6 + 5) was also incorrect (Fig. 4b).

Fig. 4
figure 4

Examples of numerical representation of the operating strategy

Full size image

Two students (S24 and S26) applied modelling with manipulatives, using the interlocking building blocks provided. To calculate the number of people who could sit at three tables, S24 set two building blocks side-by-side, looked thoughtfully at the blocks and then wrote in the number 8. He also applied multiple (manipulative-verbal) representation: after joining just two building blocks he added orally that eight people could be seated at three tables. S24’s answers to the three-table question are transcribed below.

Interviewer (I)::

Now we’re going to join three tables. How many people can we seat around them?

S24::

OK. Can I use this [pointing to the building blocks]?

I::

You can use whatever you like, yes.

S24::

[Sets two building blocks side-by-side and remains silent, thinking. Then writes in the number 8.]

I::

How did you get that number?

S24::

Well…. here… [pointing to the upper edge of the building blocks] you can fit three. Here three [pointing to the upper edge of the two-building block construction] and here also [pointing to the lower edge]. Three plus three makes six, plus two more, one here [pointing to the left side of the construction] and one here [pointing to the right side].

In terms of students’ levels of sophistication about generalising (Blanton et al., 2015), we observed that the majority of the students (18) showed reasoning typical of the pre-structural level (level 1) in their responses to the items about consecutive terms. We interpreted that this occurred when they either provided a bald answer without explaining their reasoning or used a modelling or counting strategy in which they were not observed to establish a relationship between quantities. We observed that the responses by two of the students to these items could be placed at a recursive-particular level (level 2). For example, the above-mentioned response by S22 to the term x = 3 (‘Eight there would be two more’) alludes to the recursive relationship that the student correctly applied to the previous particular term, but without evidence of having generalised it to other terms in the sequence. Two students (S14 and S23) generalised the recursive relation (level 3). For example, S23 said, ‘There are simply two more’ (see S23’s response above) without alluding to any particular term. We found that two students provided arguments that could be characteristic of a functional-particular level of thinking (level 4) when they applied the functional relationship to specific values. For example, S24 expressed the relation 3+ 3 + 2 for the particular case x = 3 (see excerpt above from the conversation with the interviewer).

8.2 Strategies in items about non-consecutive terms

Most of the students (25) answered some of the items involving the non-consecutive terms x = 8, 18 and 100 also, although there were more non answers (six) for x = 100.

The most frequent strategy for the non-consecutive term items was operating, observed in 33 instances. That strategy yielded eight correct answers. In most cases the answers were represented verbally (19). Five answers evidenced multiple representations. Examples of operating strategy and the respective representations are given below. S24 operated to reply correctly for x = 18, ‘Thirty-eight people’, explaining the answer with a row of eight building blocks (Fig. 5). Pointing to the building blocks he said ‘Here there are 18 and I see now that instead of doing it this way [with building blocks] all the time, I could multiply times two. That would give me 36 but I have to add two more here … 38’. In other words, the student multiplied the number of people on one side times two because each table has two sides (making correct use of the multiplication involved) and then added two, one at each end. S24’s reply combined operating strategy with multiple (manipulative-verbal) representation.

Fig. 5
figure 5

Operating strategy with multiple (manipulative-verbal) representation

Full size image

Other students used the operating strategies and verbal expression. S21 replied correctly for x = 18, explaining orally, ‘Thirty-eight. 18 and 18 are 36, plus 2, 38’. For x = 18, S12 answered incorrectly, explaining orally that ‘you add 10 times four’. S23 answered correctly and orally for 100 tables: ‘Here we could fit 100, here another 100. That makes 200 if we add 100 plus 100. And then there would be one here and another here. Adding it all together we get 202’.

The next most frequently used strategies were drawing and bald answering, each deployed on 14 occasions. The answers found with drawing were represented only pictorially, with no symbolic notation. Figure 6 reproduces the drawings for eight tables used by S7, S19, S21 and S25.

Fig. 6
figure 6

Four students’ pictorial representation of answers found by drawing

Full size image

Six of the drawing-based strategies led to the correct answer. S21 and S25, for instance (Fig. 6c, d) replied correctly for x = 8, drawing eight tables and correctly distributing the seating. S25 used multiple (pictorial–numerical) representation in the item for 18 tables, first drawing the tables with no chairs and then writing down the operation (addition) 18 + 18 + 2 (Fig. 7) and explaining orally: ‘Eighteen fit on this side and 18 on the other. Plus two’. In her oral explanation, the student also pointed to the drawing and when doing the operation, added in writing, ‘It can seat 38 people’.

Fig. 7
figure 7

Drawing strategy with correct answer and (pictorial–numerical) multiple representation

Full size image

Bald answering was the strategy evidenced by the 14 non-consecutive term items where no explanation was provided or where the explanations were unrelated to the procedure. When asked to calculate the number of people at eight tables, S10 first wrote in the number 10 and when asked to explain, drew one table arranging the seats in a manner unrelated to the problem as depicted on the blank questionnaire (Fig. 8).

Fig. 8
figure 8

S10’s incorrect answer for the specific case involving eight tables

Full size image

Several students who used other strategies for some non-consecutive terms replied correctly to the item with x = 18 by operating. S24 resorted to modelling with manipulatives for the consecutive terms and the non-consecutive term x = 8, but for x = 18 switched to an operating strategy and answered correctly. For values of x = 18 and higher, S21 and S25 likewise replaced drawing with operating as a strategy, correctly in both cases.

In the case of items involving non-consecutive terms, the evidence of recursive levels (both particular and general) disappeared to give way to others of a functional type. In particular, the operating strategies that yielded correct results (e.g., those of S21, S23 and S24) showed a type of reasoning characteristic of the particular-functional level (level 4), since they described relationships between specific cases without generalising across all values. The modelling and counting strategies showed pre-structural reasoning (level 1), as they established no relationships between quantities.

8.3 General term

Six students (S14, S16, S21, S24, S25 and S26) expressed a general rule when answering the item involving the general term, although only three of them (S21, S24 and S25) generalised the correct functional relationship (see Table 2). In all three cases the student referred to the context of the problem, mentioning the number of tables or seats or pointing to his/her own drawing. S21 explained, ‘You count one side, which is the same as the number of tables, multiply it by two and then add the two on the ends’. Two of the three students who expressed an incorrect rule made no reference to the context of the problem. S14 said ‘You have to multiply times 10’.

The strategy most frequently deployed for the general item was bald (i.e., unexplained) answering. Some students, even after having identified a rule to answer the items involving specific values, failed to generalise the rule in the respective item. In the specific cases involving four or more tables, S17 added t + t, t being the number of tables, but when asked ‘If you know how many tables there are, how can you figure out the number of people who can sit around them?’, he replied in writing, ‘Lots of people can sit there, I see it in my head’.

The bald answering strategy failed to yield a single correct reply. Most of the students using it gave apparently random, unexplained and unrepresented answers. S5, for instance, wrote ‘00,000,001’ and replied orally, ‘A trillion’.

The next most frequent strategy, operating, was observed on seven occasions. It was the one used by the three sole students (S21, S24 and S25) who reasoned correctly in this item. S25 wrote on the questionnaire, ‘If you know the number of tables, you know that there’s the same number on this side, then you add that up and count the ones on the ends’.

S20 used operating as a strategy by particularising with the term 100. Although initially claiming not to know the answer, at the interviewer’s insistence the student replied orally, ‘First 100 times two. Then the total plus two more’. The other students who used the operating strategy also replied incorrectly. S12’s oral reply was, ‘Four people can sit around one table. And I add it up… and whatever the answer is’.

Two students used counting as a strategy. S16 replied orally that ‘you have to count two by two for each table’. Similarly, S26 also answered orally, expressing an incorrect rule: ‘You need to count three by three’.

One student (S10) used drawing for the general case item, depicting one table and the number of seats around it that fit on the drawing (Fig. 9).

Fig. 9
figure 9

S10’s incorrect answer to the general case item

Full size image

In terms of the levels defined by Blanton et al. (2015), we found one student (S16) who gave a general recursive-level response (level 3) when answering the general term question. S16 generalised the correct recurrence relationship, expressing it as ‘Count two by two for each table’ (see above). We also identified functional-particular responses (level 4) by student S20 (see response above), since he relied on the previous particular case of 100 tables to answer the general term. The three students who generalised (S21, S24 and S25) showed reasoning at different levels. On the one hand, S25’s answer could be placed at level 5 (primitive functional-general), since she expressed the functional relationship by alluding to the context but without describing the mathematical transformation. The answers by S21 (see above) and S24 showed a reasoning typical of level 6 (emergent functional-general) because, although both students expressed the rule using mathematical operations, they referred only to one of the quantities (the number of tables).

As in previous studies using this framework (e.g., Stephens et al., 2017), we noticed responses that, although incorrect, nevertheless included some indications of functional thinking. For example, S26 generalised an incorrect recursive relationship: ‘You have to count three by three’. In such cases, the responses were not assigned to any particular level.

8.4 General overview

We next present details of the students’ performance throughout the resolution of the task, in order to provide an overview of their use of strategies. Figure 10 shows the trajectory of the students who showed correct answers at the beginning of the questionnaire.

Fig. 10
figure 10

Strategy use trajectory throughout the task by participants

Full size image

As shown in the figure, 16 participants began solving consecutive items of the questionnaire correctly. Specifically, 12 students successfully deployed the modelling strategy (with either drawing or manipulatives) when solving consecutive terms. Five of the students continued to use this strategy correctly when moving on to non-consecutive terms and managed to advance to the operating strategy, which allowed them to obtain the correct answer. Of these five students, three generalised using the operating strategy. It is interesting to note that three of the students (S23, S24 and S25) who transitioned from modelling to operations successfully in the non-consecutive terms evidenced a mixed-type strategy when solving the x = 18 term. For example, S24 combined the use of manipulatives with a multiplicative operation (see Fig. 5). In a similar vein, S25 combined her drawing of the 18 tables with the operation 18 + 18 + 2 = 38 (see Fig. 7). Both students maintained their use of the operating strategy until the general term, which they solved correctly. The remaining seven students who began using modelling either continued to use this strategy (unsuccessfully) or moved to operating strategies (also unsuccessfully) and failed to generalise.

Four students answered the consecutive-term items correctly using bald answer strategies. One of them switched to a modelling strategy with manipulatives on the non-consecutive terms, which he successfully employed until term x = 18. The remaining three deployed incorrect strategies based on operations or counting. None of the four who started out using bald answer as a strategy succeeded in generalising.

The remaining 10 participants did not answer any of the questionnaire items correctly. Among the strategies they used, a predilection for operations and bald answer strategies were observed. The students who used operations generally added the numbers in the statement. Those who used the bald answer strategy either provided one of the numbers in the statement as a solution or gave apparently random answers. In general, all these students maintained the same type of strategy throughout the whole questionnaire.

9 Discussion

In this section we analyse the results described above and offer a discussion of our conjectures on their implications in connection with the traits characteristic of ASD students.

Whereas also mainstream education students experience difficulty when asked to generalise (Hidalgo-Moncada & Cañadas, 2020), according to the findings described above, the ASD participants in this study deployed a variety of strategies, through which a few correctly generalised the function 2x + 2. Although by and large the differences revealed by a comparison of their success rates to those reported for mainstream students were narrower than expected, some of the most prominent are described in greater detail in this section.

These ASD students frequently used modelling with manipulatives and drawing-based strategies, commonly deployed as well by somewhat younger mainstream students (Cañadas & Fuentes, 2015). In particular, all the participants in this study who were able to solve the consecutive and non-consecutive terms correctly used a modelling strategy at some point in the questionnaire (see Fig. 10). Five of them managed to advance to operating strategies successfully as the terms increased.

Particularly striking was the frequency with which the bald answering strategy was deployed, even when the students were prompted by the interviewer to explain how they found what they deemed to be the solution. In studies with mainstream students of similar ages (Merino et al., 2013) bald answering was a strategy less frequently observed except in items involving small quantities. Students’ failure to explain their reasoning in this study, even after prompting, might be attributable to the communication difficulties that characterise autism spectrum disorder (APA, 2013).

According to the levels of functional thinking proposed by Blanton et al. (2015), it can be deduced from the answers and strategies employed that quite a few students did not recognise the relationship between quantities (pre-structural level). Most of those who showed an understanding of the relationship between quantities remained at a recursive-particular level, identifying the recurrence relationship for particular cases. Three students generalised the recurrence relationship (level 3), and another three generalised the functional relationship and did so at primitive or emergent functional-general levels (levels 5 and 6 respectively).

These results differ from those found by Blanton et al. (2015) in that students with ASD achieved lower levels than mainstream students. Even the three students who generalised correctly did not reach the ‘functions as object’ level (level 8). However, the assignment of levels to the participants in this study should be considered with caution. Firstly, our research was exploratory and did not include instructional sessions, while Blanton et al. followed a teaching experiment methodology in which students received eight weeks of instruction. Secondly, the levels proposed by Blanton et al. (2015) took into account aspects of language (how students expressed the relationships, and the quantities to which they referred) when assigning students’ answers to particular levels, which is one of the abilities most affected in people with ASD (APA, 2013). Thus, students with ASD may be identifying relationships between quantities but not expressing them explicitly due to their language difficulties. As previous research shows (Ingelin et al., 2021), students with ASD are likely to struggle with the communication skills needed to explain their thinking, particularly when engaged in conversations about mathematics that require providing explanations of their reasoning.

The three participants who found the functional relationship were in 6th grade (11- and 12-year-olds), which is consistent with earlier research on generalisation (Pinto & Cañadas, 2021), where students over 10 were observed to be able to generalise. In the study by Pinto and Cañadas (2021), 19 of the 24 participants generalised, 15 of them correctly. Although contextualisation was not the focus here, the only students who generalised correctly in our study alluded to the context of the task. This result is in line with that of Polo-Blanco et al. (2021), who reported greater engagement and success in problems when students contextualised their resolutions in situations familiar to them.

Some of the students who did not find the correct functional relationships did discover a rule when working with the specific terms. However, they failed to apply it to the item in the general case. S17, for instance, verbalised the rule in all the specific cases whereby the number of tables was to be multiplied by two. However, he replied to the question ‘How do you know how many people can be seated around the tables?’ by saying, ‘I see it in my head’. That answer might suggest a literal understanding and use of language, a limitation characteristic of autism spectrum disorder (Happé, 1993). Other examples of answers to the general item included ‘counting and thinking’ (S15) and ‘for the places that fit around it’ (S22). Those two students may have been replying to the question, ‘How do you know that?’ with arguments illustrative of their reasoning, or simply describing the general seating arrangement, making no attempt to associate it with the functional relationship involved. Which of the two possibilities was the case is difficult to determine, however, for answers of this nature have also been observed in research with mainstream students (Pinto & Cañadas, 2021).

Focusing on the characteristics common to people with autism, participants’ frequent choice of drawing as a strategy and its pictorial representation to perform the task support Grandin’s (1995) premise that many ASD people think visually. Drawing was also the strategy that led to the highest rate of correct answers, likewise consistent with the idea that people with the disorder are able to reason through images or visual systems. Those findings are consistent with earlier studies on ASD students’ strategies (Goñi-Cervera et al., 2021), which revealed their preference for the use of drawings. On occasion, drawing helped the students progress toward more sophisticated strategies, further attesting to the benefit they derived from the visual support afforded by that strategy.

As noted, moreover, some of the same behaviours have been observed in non-ASD students. Very young mainstream students also find it difficult to generalise (Hidalgo-Moncada & Cañadas, 2020). Similarly, students with mathematical learning difficulties exhibit less flexibility in the use of strategies than students without such difficulties (Ostad, 1997).

10 Conclusions

In this study we identified and described 26 ASD students’ functional reasoning. This research contributes to two areas scantily researched to date, namely, functional thinking by ASD-diagnosed primary education students, and research on such students’ mathematics skills in general.

Previous studies on mathematical achievement in students with ASD without intellectual disabilities, like the participants of this study, highlighted the characteristic heterogeneity of the disorder: while a small percentage show computation and problem-solving abilities similar to those of their typically developing peers, a large majority show lower performance in those areas (Bae et al., 2015; Chen et al., 2019). Although the exploratory nature of our study does not enable the results to be extrapolated, the findings do point to a similar picture regarding functional thinking. Namely, few students managed to generalise the functional relationship, compared to results of previous research with mainstream students of similar ages (Pinto & Cañadas, 2021). In terms of the strategies employed, although the same types of strategies were observed as those identified in mainstream students, unsophisticated strategies predominated, in line with other studies on problem-solving strategies with students with ASD (Bae et al., 2015; Polo-Blanco et al., 2021).

The present findings may consequently shed light on the design of possible teaching methods to help ASD students develop functional thinking. As has been shown in the case of arithmetic operation, students with mathematical difficulties and/or ASD might need explicit instruction on the use of strategies (Polo-Blanco & González, 2021), since they may not acquire strategies spontaneously, as mainstream students generally do (Ostad, 1997). Given that the most successful strategy among the participants was modelling, instruction could build on this and help ASD students move toward operating strategies. In particular, explicit instruction could be carried out in mixed-type strategies, similar to those employed by some of the participants who generalised. Thus, operating strategies could be introduced for small terms in a comprehensive way by relying simultaneously on modelling, thus helping students move towards more distant terms and generalisation.

Another approach, successfully applied in other studies involving pupils with autism (Polo-Blanco et al., 2021), might be to contextualise tasks to situations familiar to students. Given that according to one premise (Grandin, 1995) many ASD students think visually, particular emphasis might be placed on the use of visual resources when teaching early algebra to this community.

Therefore, more research is needed that focuses on implementing instruction adapted to ASD (e.g., through the use of varied tasks, visual support, explicit instruction). Such instruction is likely to help students who have shown poorer performance, as well as allow researchers to explore what levels those who have managed to generalise are able to reach. Through instructional studies such as that of Blanton et al. (2015), and considering these adaptations, ASD students could be guided in identifying relationships and helped to express relationships, which would provide a more accurate picture in terms of the levels they display (Blanton et al., 2015).

We would like to highlight that identifying and being able to work with these 26 children with ASD in Spain required considerable effort, since they belonged to 19 different schools and we carried out the work outside their regular classrooms. The varied school backgrounds provided an additional richness to this study. The information resulting from this study on the possible relationship between performing tasks that involve geometric patterns and the traits characteristic of ASD may prove useful for curricular adaptations. The present findings contribute to an understanding of learning in ASD students, a key to delivering effective teaching. That in turn should lead to improvements in their academic performance and therefore to a more independent and rewarding adult life (Wei et al., 2015).